Решение 3 страница

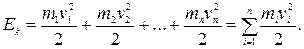
Учитывая связь между угловой и линейной скоростями, получим:

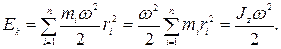(4.9)

Сопоставление формулы (4.9) с выражением для кинетической энергии тела, движущегося поступательно со скоростью v, показывает, что момент инерции является мерой инертности тела во вращательном движении.

Если твердое тело движется поступательно со скоростью v и одновременно вращается с угловой скоростью ω вокруг оси, проходящей через его центр инерции, то его кинетическая энергия определяется как сумма двух составляющих:

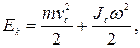(4.10)

где v_c – скорость центра масс тела; J_c - момент инерции тела относительно оси, проходящей через его центр масс.

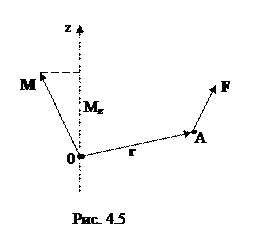
Моментом силы относительно неподвижной оси z называется скалярная величина M_z, равная проекции на эту ось вектора 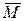момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента M_z не зависит от выбора положения точки 0 на оси z.

Если ось z совпадает с направлением вектора 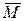, то момент силы представляется в виде вектора, совпадающего с осью:

Найдем выражение для работы при вращении тела. Пусть сила приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором 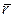. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.

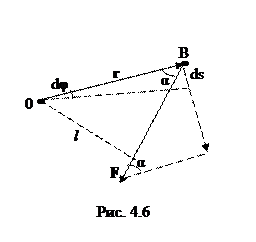При повороте тела на бесконечно малый угол 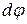точка приложения В проходит путь 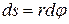, и работа равна произведению проекции силы на направление смещения на величину смещения:

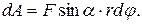
Учитывая, что 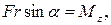можно записать 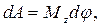где M_z - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.

Работа при вращении тела идет на увеличение его кинетической энергии:

где 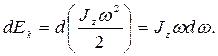Тогда 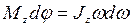, или 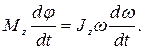Учитывая, что получим

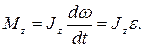(4.11)

Уравнение (4.11) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

4.4. Закон сохранения момента импульса

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса L_z не зависит от положения точки 0 на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью 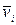. Скорость 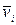и импульс 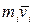перпендикулярны этому радиусу, т.е. радиус является плечом вектора 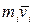. Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен

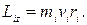
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:

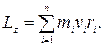
Учитывая связь между линейной и угловой скоростями (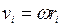), получим следующее выражение для момента импульса тела относительно неподвижной оси:

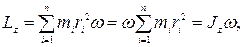(4.12)

т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцировав выражение (4.12) по времени, получим:

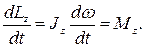(4.13)

Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.

Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем:

если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.

Действительно, если 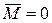, то , откуда

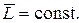(4.14)

Другими словами, момент импульса замкнутой системы с течением времени не изменяется.

Из основного закона динамики тела, вращающегося вокруг неподвижной оси z (уравнение 4.13), следует закон сохранения момента импульса тела относительно оси:

если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если M_z =0, то 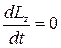, откуда

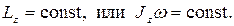(4.15)

Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.

Справедливость закона сохранения момента импульса относительно неподвижной оси вращения можно продемонстрировать на опыте со скамьей Жуковского. Скамьей Жуковского называется горизонтальная площадка, свободно вращающаяся без трения вокруг неподвижной вертикальной оси ОО₁. Человек, стоящий или сидящий на скамье, держит в вытянутых руках гимнастические гантели и приводится во вращение вместе со скамьей вокруг оси ОО₁ с угловой скоростью 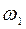. Приближая гантели к себе, человек уменьшает момент инерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения возрастает. Тогда по закону сохранения момента импульса относительно оси ОО₁ можно записать:

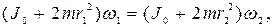(4.16)

где 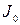- момент инерции человека и скамьи; 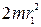и 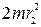- моменты инерции гантелей в первом и втором положениях; m – масса одной гантели; r₁, r₂ – расстояния от гантелей до оси ОО₁.

Изменение момента инерции системы связано с изменением ее кинетической энергии:

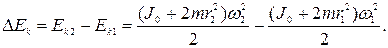
Используя выражение для , полученное из (4.16)

,

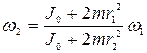после преобразований получим:

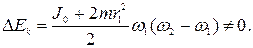
Это изменение кинетической энергии системы численно равно работе, совершенной человеком при перемещении гантелей.

В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.

Таблица 4.2

Поступательное движение	Вращательное движение
Масса m	Момент инерции Jz
Скорость	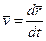Угловая скорость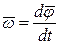
Ускорение	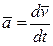Угловое ускорение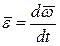
Сила	Момент силы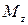
Импульс	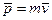Момент импульса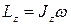
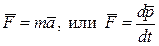
Основное уравнение динамики:	Основное уравнение динамики:
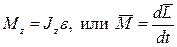
Работа	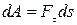Работа вращения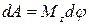
Кинетическая энергия	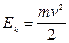Кинетическая энергия вращения

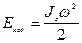
Краткие выводы

· Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

· Момент инерции тела относительно оси вращения – это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:

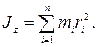
· Момент инерции тела J_z относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

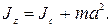
· При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:

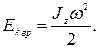
· Из сравнения формул 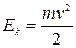и 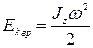следует, что момент инерции – мера инертности тела при вращательном движении.

· Работа вращения тела идет на увеличение его кинетической энергии и определяется выражением 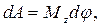где M_z – момент сил относительно оси вращения z.

· Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:

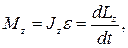
где L_z – момент импульса твердого тела относительно оси z.

· В замкнутой механической системе момент внешних сил относительно неподвижной оси M_z =0 и 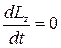, откуда L_z =const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.

Вопросы для самоконтроля и повторения

1. Что называется моментом инерции тела? Какова роль момента инерции во вращательном движении?

2. Сформулируйте теорему Штейнера. От чего зависит момент инерции тела?

3. Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?

4. Что такое момент импульса твердого тела? Как определяется направление момента импульса?

5. Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси? Как определяется работа при вращении тела?

6. Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.

7. Сформулируйте закон сохранения момента импульса. В каких системах он выполняется?

8. Сопоставьте основные величины и уравнения динамики поступательного и вращательного движений.

Примеры решения задач

Задача 1. Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии по закону 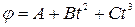, где В =2 рад/с², С =-0,5 рад/с³. Определить момент сил относительно оси вращения для момента времени t =3 c.

Дано: R =0,1 м; m =5 кг; 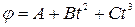рад; В =2 рад/с²; С =-0,5 рад/с³; t =3 c.

Найти: M_z.

Дата добавления: 2014-11-18