Пример. Таблица 6.2 Количество изделий, шт. Число рабочих

Таблица 6.2

Количество изделий, шт.	Число рабочих
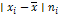
			2,16	4,32
			1,16	5,80
			0,16	1,44
			0,84	4,20
			1,84	7,36
Итого			-	23,12

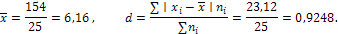
6.2. Дисперсия и её свойства

Основными обобщающими показателями вариации в статистике являются дисперсия и среднее квадратическое отклонение.

Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается S². В зависимости от исходных данных дисперсия может вычисляться простая или взвешенная:

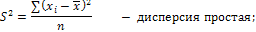
Свойства дисперсии:

1.Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.

2.Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.

3. Уменьшение или увеличение каждого значения признака в какое-то число раз k соответственно уменьшает или увеличивает дисперсию в раз, а среднее квадратическое отклонение - в k раз.

4.Дисперсия признака равна разности между средним квадратом значений признака и квадратом средней:

Пример. Имеются данные о распределении магазинов по объёму товарооборота.

Таблица 6.3

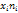
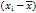
Объем товарооборота, млн.руб.	Количество магазинов		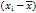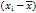	^2	^2
До 1			-4,89	23,91	95,64
1-3			-3,39	11,49	34,47
3-5			-1,39	1,93	9,65
5-7			0,61	0,37	4,07
7-9			2,61	6,81	54,48
Свыше 9			4,61	21,25	42,50
Итого			-	-	240,81

Определить дисперсию.

Решение. Рассчитаем дисперсию двумя способами:

1) по формуле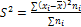

2) по формуле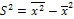

Таблица 6.4

Объем товарооборота, млн.руб.	Количество магазинов		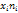^2	^2
До 1			0,25
1-3
3-5
5-7
7-9
Свыше 9
Итого			-

ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

(Небольшое расхождение связано с округлением в расчетах).

Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Оно представляет собой корень квадратный из дисперсии и выражается в тех же единицах измерения, что и признак.

Среднее квадратическое отклонение простое:

Среднее квадратическое отклонение взвешенное:

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.

Дата добавления: 2014-11-18