Ранговые коэффициенты корреляции

Ранговые коэффициенты корреляции также не учитывают каждое значение признаков x и y, а рассматривают номера их мест, т.е. ранги, занимаемые в каждом ряду по возрастанию или убыванию.

Коэффициент корреляции рангов Спирмана:

где 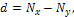т.е. разность рангов каждой пары значений x и y;

n – число наблюдений.

Коэффициент корреляции рангов Кендала:

Рассмотрим порядок расчёта данных коэффициентов:

1. Ранжируются значения x и y, т.е. определяются .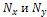

2.Значения располагаются в порядке возрастания, а значения - в соответствии со значениями x в исходных данных.

3.Для каждого значения подсчитывается число следующих за ним рангов более высокого порядка и их общее количество обозначается P.

4.Аналогично для каждого значения подсчитывается число следующих за ним рангов, меньших по значению, и их общее количество обозначается

5. Определяется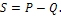

Пример. По данным 10 предприятий с помощью коэффициентов Спирмана и Кендала измерить тесноту зависимости между себестоимостью единицы продукции (x), руб., и потреблением электроэнергии (y), кВт/ч.

Таблица 9.8

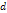
x	y					Баллы
				-1 -1 -1 -1 -2		-	-
						P = 39	= 6

Решение. Ранжируем значения x и y (графы 3-4).

Определяем коэффициент корреляции рангов Спирмана:

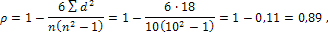
т.е. связь между x и y прямая и высокая.

Для расчёта коэффициента Кендала определяем :

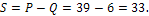
Рассчитываем коэффициент корреляции рангов Кендала:

Обычно коэффициент Кендала всегда меньше коэффициента Спирмана, причём

Рассмотрим пример расчёта коэффициентов Спирмана и Кендала, когда некоторые значения показателей совпадают, т.е. ранги повторяются.

Пример. С помощью ранговых коэффициентов корреляции по 8 предприятиям определить тесноту зависимости между стоимостью ОПФ (x), млн. руб., и прибылью (y), млн. руб.

Таблица 9.9

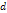
x	y					Баллы
15,4 15,6 15,6 17,3 17,9 18,5 19,4 20,8	1,2 1,8 1,5 2,6 2,6 2,6 3,7 2,9	2,5 2,5		-0,5 0,5 -1 -1	0,25 0,25	-	-
					4,5	P = 23	= 2

В случае повторяющихся рангов коэффициент Спирмана вычисляется по той же формуле:

Коэффициент Кендала в данном случае определяется по другой формуле:

где показатели, корректирующие максимальную сумму баллов и определяемые по формуле где число повторяющихся рангов в соответствующем ряду x и y.

Для данного примера

Общая сумма баллов:

Рассчитываем коэффициент корреляции рангов Кендала:

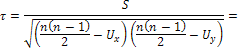
По вычисленным коэффициентам можно сказать, что связь между стоимостью ОПФ и прибылью очень высокая.

Дата добавления: 2014-11-18