Ошибки выборки

Ошибкой выборки называются пределы отклонений характеристик генеральной совокупности от характеристик выборочной совокупности.

Различают среднюю и предельную ошибки выборки.

Средняя ошибка выборки (μ) характеризует среднюю величину отклонения показателя выборочной совокупности от соответствующего показателя генеральной совокупности.

При повторном отборе средняя ошибка выборки определяется по формулам:

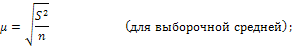
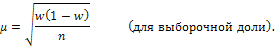
Средняя ошибка выборки при бесповторном отборе рассчитывается по формулам:

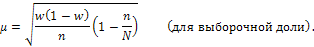
Согласно закону нормального распределения, вероятность появления такой величины ошибки выборки в данном случае равна 0,683. На практике часто возникает необходимость получения данных с большей вероятностью, поэтому рассчитывают предельную ошибку выборки.

Предельной ошибкой выборки (∆) называется отклонение выборочной характеристики от генеральной.

Предельная ошибка выборки определяется по формуле:

где 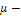средняя ошибка выборки;

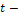коэффициент кратности, или коэффициент доверия, который зависит от заданной вероятности P.

P	t
0,683 0,866 0,954 0,988 0,997	1,0 1,5 2,0 2,5 3,0

При повторном отборе предельная ошибка выборки определяется по формулам:

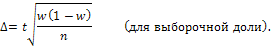
Предельная ошибка выборки при бесповторном отборе рассчитывается по формулам:

Также рассчитывается относительная величина предельной ошибки:

Относительную ошибку также можно вычислить по формуле:

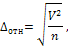
где коэффициент вариации.

Если 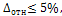то выборка считается репрезентативной.

После расчёта предельной ошибки выборки определяются доверительные границы генеральной совокупности для изучаемого показателя:

t wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/></w:rPr><m:t>,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="002F4108"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

Пример. Из партии товара в 4500 единиц было обследовано 300 шт., из которых 4,5% оказались бракованными. С вероятностью 0,954 определить пределы бракованной продукции во всей партии товара, если дисперсия составила 3,2.

Решение. При заданной вероятности коэффициент доверия составляет 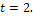Рассчитываем предельную ошибку выборки для бесповторного отбора:

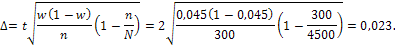
Определяем генеральную среднюю

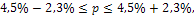
т.е. доля бракованной продукции во всей партии товара находится в пределах от 2,2% до 6,8%.

Дата добавления: 2014-11-18