Уравнение прямой. Условия параллельности и перпендикулярности прямых

Ряды. Радиус сходимости. Абсолютная и условная сходимость.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Рассматриваются числовые ряды двух видов

· вещественные числовые ряды — изучаются в математическом анализе;

· комплексные числовые ряды — изучаются в комплексном анализе;

Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.

Числовые ряды применяются в качестве системы приближений к числам

В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.

Уравнение вида

(1)

называется общим уравнением прямой.

Угол 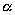, определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:

Уравнение называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением

,

то ее угловой коэффициент определяется по формуле

.

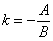Уравнение является уравнением прямой, которая проходит через точку 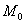(, ) и имеет угловой коэффициент k.

Если прямая проходит через точки (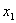, ), (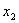, 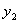), то ее угловой коэффициент определяется по формуле

.

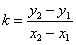Уравнение

является уравнением прямой, проходящей через две точки (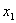,) и (, ).

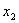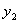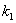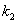Если известны угловые коэффициенты и двух прямых, то один из углов между этими прямыми определяется по формуле

.

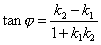Признаком параллельности двух прямых является равенство их угловых коэффициентов:

.

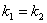Признаком перпендикулярности двух прямых является соотношение

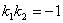, или .

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.

Функция двух переменных. Частные производные, полный дифференциал.

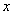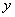Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами.

Пример: – функция двух переменных.

Иногда используют запись .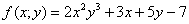

С геометрической точки зрения функция двух переменных чаще всего представляет собой поверхность трехмерного пространства (плоскость, цилиндр, шар, параболоид, гиперболоид и т. д.). Но, собственно, это уже больше аналитическая геометрия, а у нас на повестке дня математический анализ, который никогда не давал списывать мой вузовский преподаватель является моим «коньком».

Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:

Пример 1

Найти частные производные первого и второго порядка функции

Сначала найдем частные производные первого порядка. Их две.

Обозначения:
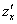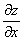или – частная производная по «икс»
или – частная производная по «игрек»

Начнем с 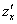. Когда мы находим частную производную по «икс», то переменная 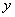считается константой (постоянным числом).

Решаем. На данном уроке я буду приводить полное решение сразу, а комментарии давать ниже.

Комментарии к выполненным действиям:

(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.

Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если Вы где-нибудь нарисуете «штрих» без 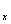, то преподаватель, как минимум, может поставить рядом с заданием 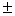(сразу откусить часть балла за невнимательность).

Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.

(2) Используем правила дифференцирования 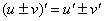, 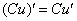. Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как 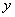считается константой, а любую константу можно вынести за знак производной, то 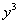мы выносим за скобки. То есть в данной ситуации 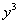ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как 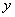константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».

(3) Используем табличные производные и .

(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.

Теперь . Когда мы находим частную производную по «игрек», то переменная 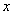считается константой (постоянным числом).

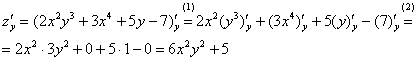
(1) Используем те же правила дифференцирования 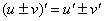, 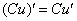. В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку 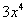– уже константа.

(2) Используем таблицу производным элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для 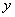(да и вообще почти для любой буквы). В частности, используемые нами формулы выглядят так: и .

Итак, частные производные первого порядка найдены

Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:

1) Когда мы находим частную производную 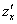, переменная 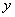считается константой.

2) Когда мы находим частную производную , переменная 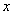считается константой.

3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (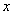, 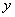либо какой-нибудь другой), по которой ведется дифференцирование.

Шаг второй. Находим частные производные второго порядка. Их четыре.

Обозначения:
или – вторая производная по «икс»
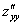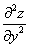или – вторая производная по «игрек»
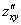или 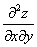– смешанная производная «икс по игрек»
или 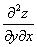– смешанная производная «игрек по икс»

В понятии второй производной нет ничего сложного. Говоря простым языком, вторая производная – это производная от первой производной.

Для наглядности я перепишу уже найденные частные производные первого порядка:

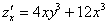
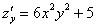
Сначала найдем смешанные производные:

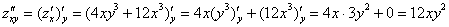
Как видите, всё просто: берем частную производную 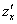и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

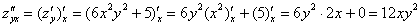
В практических примерах можно ориентироваться на следующее равенство:

Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс».
Никаких изобретений, берем 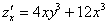и дифференцируем её по «икс» еще раз:

Аналогично:

Следует отметить, что при нахождении , 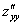нужно проявить повышенное внимание, так как никаких чудесных равенств для их проверки не существует.

Дата добавления: 2014-11-08