Устройство и принцип действия маятника Обербека

Теория лабораторной работы

Аналогия между поступательным и вращательным движениями

Основное уравнение динамики вращательного движения

Уравнение (3) M = d L / dt называется основным уравнением динамики вращательного движения: скорость изменения момента импульса тела, вращающегося вокруг неподвижной точки, равна результирующему моменту относительно этой точки всех внешних сил, приложенных к телу.

Из уравнений (1) и (3) следует М = d ( I ω) / dt = I d ω / dt = I e,

или e = М / I.

Угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ, линейной скорости
v – угловая скорость w, линейному (касательному) ускорению а – угловое ускорение ε.

Поступательное движение	Вращательное движение
Кинематические характеристики движения
Путь	S	м	Угол поворота	j	рад
Время	t	с	Период	Т	с
Скорость	v	м/с	Угловая скорость	w	рад/с
Ускорение	a	м/с^2	Угловое ускорение	e	рад/с^2
Поступательное движение	Вращательное движение
Динамическиехарактеристики движения
Масса	m	кг	Момент инерции	J	кг × м^2
Сила	F	Н	Момент силы	M	Н × м
Импульс	p	кг×м/с	Момент импульса	L=J×w	кг × м^2 /с
Второй закон Ньютона	F=ma; F=dp/dt	Уравнение динамики вращательного движения	M=J×e; M=dL/dt
Работа	dA=F×dS	Дж	Работа	dA=M×dj	Дж
Кинетическая энергия	EK=(mv^2)/2	Дж	Кинетическая энергия	EKВР=(Jw^2)/2	Дж
Мощность	N=FV	Вт	Мощность	N=М×w	Вт

Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.

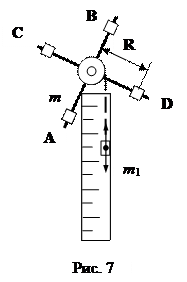
В работе используется крестообразный маятник Обербека (рис.7), который состоит из двух взаимно перпендикулярных стержней АВ и CD, ввинченных в шкив К. Крестовина может вращаться при падении груза Р, привязанного к нити, намотанной на шкив. По стержням АВ и CD могут перемещаться четыре груза, массы m которых одинаковы.

Момент инерции груза определится формулой

I = m R ²,

где R – расстояние от груза до оси вращения.

Если на шкив намотать нить и к ее концу прикрепить груз, то при его падении маятник будет вращаться с угловым ускорением e, а сам груз будет двигаться с линейным ускорением а. Вращающий момент будет равен произведению силы натяжения нити F_н на радиус шкива r: M = F_н r. Движение груза вниз происходит под действием двух сил: силы тяжести (F ₁= m ₁ g или F ₂ = m ₂ g), направленной вниз, и силы натяжения нити F_н, направленной вверх. Результирующая сила, сообщающая ускорение, будет равна

ma = mg – F_н,

откуда сила натяжения F_н = m (g – a)

Момент этой силы относительно оси вращения

M = m(g – a) r (5)

где r – радиус шкива.

Если за время t груз упал с высоты h, то ,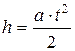

откуда линейное ускорение .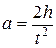

Формулу (5) можно записать в виде

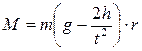, (6)

а угловое ускорение 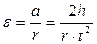. (7)

Дата добавления: 2014-11-18