Момент инерции. Связь линейных и угловых характеристик

Связь линейных и угловых характеристик

Равнопеременное вращение

Если угловое ускорение ε = const, то вращательное движение называется равнопеременным. Равнопеременное вращение характеризуется следующими уравнениями:

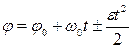и w = w₀ + e t,

w ₀ и j ₀ – угловая скорость и угол поворота тела в начальный момент t ₀=0,

w и j – в момент времени t. При ускоренном вращении в этих уравнениях выбирается знак «+», а при замедленном – знак «–».

Если точка тела отстоит от оси вращения на расстоянии r, то за время dt она проходит путь

dS = d j × r

Скорость точки

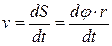, или v = w ×r

При вращении тела тангенциальное ускорение его точки

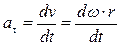, или

a _t =e×r

Нормальное ускорение точки тела

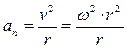, или

/a _n =w ²×r

Полное ускорение, как указывалось ранее, определяют по формуле

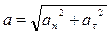
Момент инерции - скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.

Единица измерения СИ: кг·м². Обозначение: I или J.

Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы относительно этой оси. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело.

Момент инерции элементарной (точечной) массы m_i, отстоящей от оси на расстоянии r_i, равен:

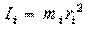
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

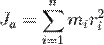где:

m_i — масса i -й точки,

r_i — расстояние от i -й точки до оси.

,

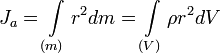где:

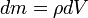— масса малого элемента объёма тела ,

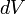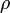— плотность,

— расстояние от элемента 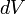до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

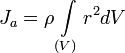
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра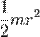
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра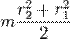
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс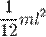
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец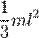
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы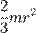
	Шар радиуса r и массы m	Ось проходит через центр шара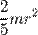

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями:

J = J_c + ma².

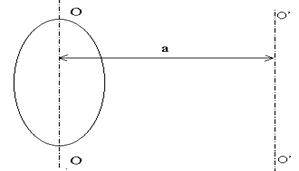
Рис. 3

где — полная масса тела (рис. 3).

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

.

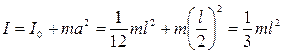
Дата добавления: 2014-11-18