
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ 2. 2 страница
|
|
|
|
f=10 в (2, 0, 1, 0, 0, 0, 0)
Найдем решение прямой задачи.
Z=10 в (5, 1, 2)
3.2. Открытая и закрытая модели транспортной задачи
Формулировка и основные понятия для транспортной задачи представлены в вопросе 1.8.
Определение 1: Модель транспортной задачи называется закрытой, если суммарный объем груза имеющегося у поставщиков равен суммарному спросу потребителей т.е.

Определение 2: Если для транспортной задачи выполняется одно из условий:
 или
или 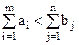
то модель задачи называется открытой.
Для разрешимости транспортной задачи с открытой моделью необходимо преобразовать ее в закрытую. Так при выполнении первого условия необходимо ввести фиктивный (n+1) пункт назначения ( ), т.е. в матрице задач предусматривается дополнительный столбец. Спрос фиктивного потребителя полагаем равный небалансу т.е.
), т.е. в матрице задач предусматривается дополнительный столбец. Спрос фиктивного потребителя полагаем равный небалансу т.е.
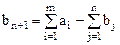 ;
;
все тарифы одинаковы, чаще всего равны нулю  (
(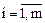 ).
).
Аналогично при выполнении второго условия вводится фиктивный поставщик, запас груза у которого равен
 ;
;
все тарифы дополнительной строки распределительной таблицы равны нулю 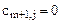 (
(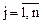 ).
).
При преобразовании открытой задачи в закрытую, целевая функция не меняется т.к. все слагаемые соответствующие дополнительным перевозкам равнялись нулю.
Теорема 1: (о ранге матрицы) Ранг матрицы А транспортной задачи на единицу меньше чем числа уравнений r(A)=m+n-1.
Замечание: Эта теорема говорит о том, что при решении любой транспортной задачи в распределительной таблице должна быть заполнена m+n-1 ячейка.
3.3. Построение начального опорного плана. Правило "Северо-западного угла"
Построение начального опорного плана для транспортной задачи возможно лишь для закрытой модели и может осуществляться несколькими способами. Если модель – открытая, необходимо ее преобразовать в закрытую. Рассмотрим самый простой и неточный способ построения.
Заполнение распределительной таблицы начинается с верхнего левого угла, который еще называют северо-западным. В ячейку с координатами (1,1) записывается минимальное из чисел 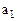 и
и 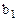 .
.
Предположим, что это 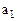 . Тогда товар первого поставщика полностью реализован и он может быть исключен из рассмотрения. Соответственная ему первая строка больше не заполняется. Следующей будем заполнять ячейку (2,1). В нее записываем наименьшее из чисел
. Тогда товар первого поставщика полностью реализован и он может быть исключен из рассмотрения. Соответственная ему первая строка больше не заполняется. Следующей будем заполнять ячейку (2,1). В нее записываем наименьшее из чисел  и
и 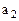 . Предположим, что минимум это число
. Предположим, что минимум это число  . тогда потребности первого поставщика полностью удовлетворены. Первый столбик может быть исключен из рассмотрения. Далее будем рассматривать ячейку с номером (2,2).
. тогда потребности первого поставщика полностью удовлетворены. Первый столбик может быть исключен из рассмотрения. Далее будем рассматривать ячейку с номером (2,2).
Если же при первом сравнении получили, что наименьшее число 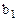 , то процесс аналогичным образом продолжается, но рассматриваем мы ячейку с номером (1,2).
, то процесс аналогичным образом продолжается, но рассматриваем мы ячейку с номером (1,2).
Пример: Решить транспортную задачу:
| B1 | B2 | B3 | ||
| A1 | v | v | ||
| A2 | v | |||
| A3 | v | |||
| A4 | v | v | ||
Модель транспортной задачи – закрытая. Символом v будем обозначать пустую ячейку. Заполненных ячеек 4+3-1=6.
Ответ: Z=11900
В некоторых случаях появляется необходимость вставки так называемой ноль-загрузки. Т.е. в ячейку проставляется 0 и она считается заполненной. Эта необходимость возникает только в том случае, когда одновременно из рассмотрения исключаются и строка и столбец одновременно. Ноль-загрузка в этом случае ставится в любую соседнюю свободную ячейку (справа или внизу).
3.4. Построение начального опорного плана. Правило минимального элемент
Сущность: рассматриваются тарифы в распределительной таблице и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику запасы которого полностью израсходованы, или столбец соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. Опорный план получаемый в результате данных содержащих m+n-1 загруженных клеток, но в процессе заполнения таблицы могут быть одновременно исключены строка и столбец. Поэтому в свободные клетки нужно записать число 0, условно считая такую клетку занятой.
| B1 | B2 | B3 | ||
| A1 | v | v | ||
| A2 | v | |||
| A3 | v | |||
| A4 | v | v | ||
Z=3*800+2*600+4*100+4*200+5*800+1*500=9300
3.5. Построение начального опорного плана. Метод Фогеля
В распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится как и в предыдущих двух методах.
| B1 | B2 | B3 | |||||||
| A1 | v | v | – | – | |||||
| A2 | v | – | |||||||
| A3 | v | ||||||||
| A4 | v | v | – | – | – | – | |||
| – | |||||||||
| – | |||||||||
| – |
Заполненных ячеек 6.
Z=3*800+2*600+4*100+4*200+5*800+1*100=8900
3.6. Метод потенциалов
Для проверки оптимальности опорного плана используют следующую теорему:
Теорема: Если план транспортной задачи является оптимальным, то ему соответствует система из m+n чисел 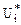 ,
,  , удовлетворяющих условиям:
, удовлетворяющих условиям:
·  - для заполненных ячеек;
- для заполненных ячеек;
· 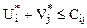 - для свободных ячеек.
- для свободных ячеек.
Эти, 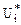 ,
,  называются потенциалами.
называются потенциалами.
Таким образом, для того чтобы определить является ли начальный опорный план оптимальным, необходимо рассчитать  и
и  , затем проверить второе неравенство для свободных ячеек.
, затем проверить второе неравенство для свободных ячеек.
Пусть дан начальный опорный план для некоторой транспортной задачи, записанный в распределительной таблице. посчитаем  и
и  .
.
Заполненых ячеек в распределительной таблице m+n-1. Если составлять уравнения 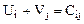 , получим m+n-1 уравнение с m+n неизвестными. n+m-1<n+m. Следовательно, система имеет бесконечно много решений. Нас устроит любое из них. Поэтому принято одну из
, получим m+n-1 уравнение с m+n неизвестными. n+m-1<n+m. Следовательно, система имеет бесконечно много решений. Нас устроит любое из них. Поэтому принято одну из  или
или  принимать равной 0.
принимать равной 0.
Замечание: Чаще всего за ноль принимают ту из переменных  или
или  , для которой в соответствующей строке или столбце больше заполненных ячеек.
, для которой в соответствующей строке или столбце больше заполненных ячеек.
После того, как  и
и  найдены, необходимо оценить оставшиеся ячейки. Для этого считают так называемые оценки свободных ячеек. Они равны:
найдены, необходимо оценить оставшиеся ячейки. Для этого считают так называемые оценки свободных ячеек. Они равны:

Для того, чтобы план был оптимален необходимо, чтобы все  для свободных ячеек были неотрицательными.
для свободных ячеек были неотрицательными.
Пример: Рассчитать потенциалы для примера в 3.4, 3.5, 3.6
| B1 | B2 | B3 | 
| ||
| A1 | v | v | |||
| A2 | v | ||||
| A3 | v | ||||
| A4 | v | v | -1 | ||
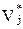
|
Вычислим оценки:
 =5-(0+2)=3>0 =5-(0+2)=3>0
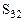 =3-(1+2)=0=0 =3-(1+2)=0=0
| 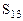 =6-(0+4)=2>0 =6-(0+4)=2>0
 =6-(3-1)=4>0 =6-(3-1)=4>0
| 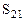 =7-(0+3)=4>0 =7-(0+3)=4>0
 =7-(4+1)=2>0 =7-(4+1)=2>0
|
Все полученные оценки неотрицательны, следовательно, опорный план оптимален, транспортная задача решена.
Ответ: Z=8900.
Ситуация, когда все оценки сразу получились неотрицательными, достаточна редка. Чаще всего план получается не оптимальным (особенно, если начальный опорный план составлять по правилу северо-западного угла.
Предположим, что. решая транспортную задачу и рассчитав оценки свободных ячеек, мы получили несколько отрицательных оценок. Выберем из них наименьшую. Пусть это будет 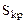 . Тогда говорят, что ячейка с номером (k,p) потенциальна, т.е. ее необходимо заполнить.
. Тогда говорят, что ячейка с номером (k,p) потенциальна, т.е. ее необходимо заполнить.
Для того, чтобы заполнить потенциальную ячейку, строят цикл.
Правила построения цикла:
1. Начальная вершина цикла – потенциальная ячейка.
2. Остальные вершины, находятся только в заполненных ячейках.
3. Ребра в вершинах образуют прямой угол.
4. Ребра могут пересекаться. Однако, точка пересечения ребер не считается вершиной.
Построенный цикл для потенциальной ячейки – единственный. Далее необходимо перераспределить груз в ячейках в рамках цикла. При этом нельзя забывать, что количество заполненных ячеек не должно изменяться. Для этого маркируют вершины цикла знаками "+" и "–". Вершина цикла, находящаяся в потенциальной ячейке, всегда имеет знак "+". В остальных вершинах знаки чередуются ("–", "+", "–", "+", …). Из "отрицательных" ячеек выбираем ту, в которой минимальная загрузка. Эту ячейку и будем освобождать от груза. Маркируем ее как пустую ячейку. Далее, к загрузке в "положительных" ячейках прибавляем значение выбранной минимальной загрузки, в "отрицательных" – вычитаем это же значение. После данной процедуры получается новый опорный план, который необходимо проверить на оптимальность.
Алгоритм решения транспортной задачи:
1. Составляем начальный опорный план (по любому правилу и методу, лучше – методом минимального элемента).
2. Считаем потенциалы  и
и  .
.
3. Рассчитываем оценки свободных ячеек ( ).
).
4. Если все оценки  - неотрицательны, то план оптимален. Задача решена. Считаем Z.
- неотрицательны, то план оптимален. Задача решена. Считаем Z.
5. В противном случае, выбираем наименьшее отрицательное значение  . Соответствующая ячейка будет называться потенциальной.
. Соответствующая ячейка будет называться потенциальной.
6. Строим цикл.
7. Маркируем вершины цикла знаками "+" и "–".
8. Выбираем наименьшую загрузку в "отрицательных" вершинах.
9. Выбранную ячейку считаем свободной.
10. Найденную минимальную загрузку прибавляем к загрузке "положительных" ячеек цикла и вычитаем из "отрицательных".
11. Получен новый опорный план. Переходим к пункту 2.
Пример: Решить транспортную задачу:

| ||||||||||
| v | v | v | v | -2 | ||||||
 6 6
 10 10
|
 3 3
| v | ||||||||
|
| v | v | |||||||

| -1 | -2 | ||||||||
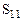 =7-(3-2)=6>0 =7-(3-2)=6>0
 =3-(3+2)=-2<0 =3-(3+2)=-2<0
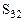 =5-(0-1)=6>0 =5-(0-1)=6>0
|  =3-(-1-2)=6>0 =3-(-1-2)=6>0
 =7-(4+3)=0=0 =7-(4+3)=0=0
 =6-(0-2)=4>0 =6-(0-2)=4>0
| 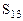 =5-(-2-2)=9>0 =5-(-2-2)=9>0
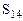 =2-(4-2)=0=0 =2-(4-2)=0=0
| ||||||||
Потенциальная ячейка – (2,3). Построим цикл. Промаркировав его, получаем две "отрицательные" ячейки: (2,1) и (3,3). Минимальная загрузка в них равна 10. Прибавляя к загрузке в "положительных" ячейках и вычитая в "отрицательных", получим новую распределительную таблицу:

| ||||||
| v | v | v | v | -3 | ||
| v | v | |||||
| v | v | -1 | ||||

|
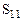 =7-(-3+4)=6>0 =7-(-3+4)=6>0
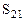 =6-(4+0)=2>0 =6-(4+0)=2>0
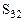 =5-(2-1)=4>0 =5-(2-1)=4>0
|  =3-(-3+2)=4>0 =3-(-3+2)=4>0
 =7-(5+0)=2>0 =7-(5+0)=2>0
 =6-(1-1)=6>0 =6-(1-1)=6>0
| 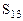 =5-(3-3)=5>0 =5-(3-3)=5>0
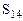 =2-(5-3)=0=0 =2-(5-3)=0=0
|
Полученный план оптимален.
Ответ: Z=2*40+2*80+3*10+1*60+3*20+2*80+0*4=550
3.7. Решение транспортных задач с ограничениями по пропускной способности
В некоторых случаях в условии транспортной задачи накладываются дополнительные ограничения на пропускную способность линии связи. Будем их обозначать  . Тогда говорят о разновидности транспортных задач – транспортных задачах с ограничениями по пропускной способности. Все ограничения записываются в левом нижнем углу ячейки. Они означают, что больше чем записано в ячейку загрузить нельзя.
. Тогда говорят о разновидности транспортных задач – транспортных задачах с ограничениями по пропускной способности. Все ограничения записываются в левом нижнем углу ячейки. Они означают, что больше чем записано в ячейку загрузить нельзя.
Решаются такие задачи обычным образом, но с дополнительными особенностями.
Алгоритм решения транспортных задач с ограничениями по пропускной способности:
1. Построение начального опорного плана можно осуществлять любым методом (правило северо-западного угла, минимального элемента, метод Фогеля). Лучше всего: по правилу минимального элемента. Особенность построения начального опорного плана заключается в следующем: в выбранную ячейку ставится минимальное из чисел  ,
,  и
и  . Если было выбрано одно из чисел
. Если было выбрано одно из чисел  или
или  , то говорят, что заполненная ячейка – базисная. Если же в ячейку записывается число
, то говорят, что заполненная ячейка – базисная. Если же в ячейку записывается число  , то ячейку назовем дополнительной. После заполнения распределительной таблицы для транспортной задачи с ограничениями по пропускной способности может остаться в некоторых столбцах и строках нераспределенный груз. В этом случае вводятся дополнительные строка и столбец, загрузка которых равна объему нераспределенного груза, а тарифы каждой ячейки, исключая (m+1, n+1), равны М. М – бесконечно большое, положительно число. В ячейке (m+1, n+1) тариф равен 0. В результате базисных переменных должно быть m+n-1.
, то ячейку назовем дополнительной. После заполнения распределительной таблицы для транспортной задачи с ограничениями по пропускной способности может остаться в некоторых столбцах и строках нераспределенный груз. В этом случае вводятся дополнительные строка и столбец, загрузка которых равна объему нераспределенного груза, а тарифы каждой ячейки, исключая (m+1, n+1), равны М. М – бесконечно большое, положительно число. В ячейке (m+1, n+1) тариф равен 0. В результате базисных переменных должно быть m+n-1.
2. Расчет потенциалов производится по базисным ячейкам. Расчет оценок свободных и дополнительных ячеек производится обычным образом. Однако, для оптимальности опорного плана необходимо, чтобы оценки дополнительных ячеек были неположительны. Для свободных ячеек оценки должны быть неотрицателтьны, а для базисных равны 0.
3. Если полученный опорный план не оптимален, то обычным образом строят цикл. производят перемещение груза по циклу и снова определяют оптимальность полученного решения.
Пример: Решить транспортную задачу с ограничениями по пропускной способности:

| ||||||
+ 10
  БП БП
| v | v | БП |
– 80
 БП БП
| -2 | |
| БП | 70ДП | v | v | v | -1 | |
 7
– 0
БП 7
– 0
БП
| БП | БП | v | + v | ||

|
Базисных переменных: 5+3-1=7. Дополнительная переменная 1.
Сосчитаем оценки:
 =8-(-2+4)=6>0 =8-(-2+4)=6>0
 =5-(2-1)=4>0 =5-(2-1)=4>0
 =3-(4+0)=-1<0 =3-(4+0)=-1<0
| 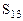 =7-(-2+2)=7>0 =7-(-2+2)=7>0
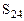 =4-(4-1)=3>0 =4-(4-1)=3>0
 =2-(3+0)=-1<0 =2-(3+0)=-1<0
|  =3-(4-1)=0=0 =3-(4-1)=0=0
 =6-(3-1)=4>0 =6-(3-1)=4>0
|
Получились две отрицательные оценки. Строим цикл.

| ||||||
| БП | v | v | БП | БП | -1 | |
| БП | 70ДП | v | v | v | ||
| v | БП | БП | v | БП | ||

|
Базисных переменных: 5+3-1=7. Дополнительная переменная 1.
Сосчитаем оценки:
 =8-(-1+4)=5>0 =8-(-1+4)=5>0
 =5-(2+0)=3>0 =5-(2+0)=3>0
 =3-(3+0)=0=0 =3-(3+0)=0=0
| 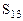 =7-(-1+2)=6>0 =7-(-1+2)=6>0
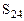 =4-(3+0)=1>0 =4-(3+0)=1>0
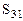 =7-(6+0)=1>0 =7-(6+0)=1>0
|  =3-(4+0)=-1<0 =3-(4+0)=-1<0
 =6-(2+0)=4>0 =6-(2+0)=4>0
|
Полученный план оптимален. Z=5*10+2*130+1*80+6*70+3*70+4*70+ +2*90+2*0=1480
Ответ: Z=1480.
3.8. Примеры задач дискретного программирования. Задача о контейнерных перевозках. Задача о назначении
Дискретное программирование – это раздел математического программирования и изучающий экстримальные задачи, в которых на искомые переменные налагаются условия целочисленности, а область допустимых решений конечна.
Дискретное программирование также называется целочисленным.
Задача о контейнерных перевозках (о рюкзаке или о бомбардировщике).
Контейнер оборудован m отсеками, вместимостью 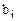 (
(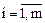 ). Для перевозки n видов продукции. Виды продукции характеризуются свойствами неделимости. Пусть
). Для перевозки n видов продукции. Виды продукции характеризуются свойствами неделимости. Пусть 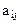 – расход i-того отсека для перевозки j-той продукции. Обозначим через
– расход i-того отсека для перевозки j-той продукции. Обозначим через 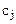 полезность единицы j-й продукции. Требуется найти план перевозки, при котором прибыль от перевозки максимизируется:
полезность единицы j-й продукции. Требуется найти план перевозки, при котором прибыль от перевозки максимизируется:
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 490; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 10
10