
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ 2. 1 страница
|
|
|
|
Способ 1.
1. Найти разрешающий элемент.
2. С помощью представленных формул преобразовать все уравнения системы ограничений.
3. Посчитать значение целевой функции.
Алгоритм действий представлен на Рис. 13.
Определение: Шаг симплексного метода, позволяющего перейти от одного опорного плана к другому, называется итерацией.
Пример: Решить симплексным методом ЗЛП:

при 

Рис. 13. Алгоритм решения задач линейного программирования на максимум (минимум), используя симплексные преобразования
Решение.
Система ограничений имеет предпочтительный вид. Можно составлять симплексную таблицу:
| БП | СБ | А | 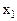
| 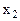
| 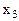
| 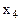
| 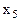
| № итерации |
| -5 | -1 | |||||||
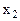
| -5 |  1 \ 1 \ 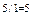
| -1 | |||||
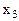
| 5 \ 
| |||||||
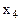
| -1 | -5 | ||||||
 -4 -4
| -1 | |||||||
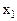
| -1 | |||||||
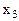
| -5 |  8 \ 8 \ 
| ||||||
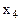
| -1 | -1 | ||||||
 -5 -5
| ||||||||
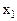
| 
| 
| ||||||
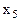
| 
| 
| ||||||
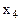
| -1 | 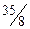
| 
| |||||

| 
|
В индексной строке последней симплексной таблицы все оценки свободных переменных положительны. Следовательно, план оптимален.
Ответ: Z=72 в (7, 0, 0, 42, 2).
2.9. Альтернативный оптимум (признак бесконечности множества опорных планов)
Из геометрической иллюстрации ЗЛП следует, что она имеет бесконечно много решений, если линия уравнения проходит через сторону прямоугольника (Рис. 14).
Для решения задачи симплексным методом ответ на вопрос: имеет ли задача бесконечно много решений, дает теорема:

Теорема: Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то ЗЛП имеет бесконечно много решений.
Следствие: Если в индексной строке симплексной таблицы, содержащей оптимальный план, все оценки соответствующие свободным переменным положительны, то найденное решение - единственное.
2.10. Признак неограниченности целевой функции
 Из геометрической иллюстрации ЗЛП видно, что задача не имеет решений, если область допустимых решений не ограничена (Рис. 15).
Из геометрической иллюстрации ЗЛП видно, что задача не имеет решений, если область допустимых решений не ограничена (Рис. 15).
Область допустимых решений неограниченна, если область неограниченна сверху для решения задач на max, неограниченна снизу – для задач на min. Ответ на вопрос о неограниченности целевой функции при решении ЗЛП симплексным методом дают следующие теоремы.
Теорема 1: Если в индексной строке последней симплексной таблицы ЗЛП на max содержится отрицательная оценка 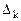 , а в соответствующем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов неограниченна сверху.
, а в соответствующем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов неограниченна сверху.
Теорема 2: Если в индексной строке последней симплексной таблицы ЗЛП на min содержится положительная оценка 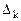 , а в соответствующем столбце переменной
, а в соответствующем столбце переменной 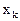 нет ни одного положительного элемента, то на множестве допустимых планов целевая функция неограниченна снизу.
нет ни одного положительного элемента, то на множестве допустимых планов целевая функция неограниченна снизу.
2.11. Понятие о вырождении. Монотонность и конечность симплексного метода. Зацикливание
Базисный план ЗЛП, записанной в предпочтительном виде невырожден, когда свободные члены всех уравнений положительны, и вырожден, если среди них имеются нули.
Определение: Каноническую ЗЛП называют невырожденной, если все ее опорные планы невырождены. Если среди опорных планов есть хотя бы один вырожденный, то задачу называют вырожденной.
Пусть ЗЛП решается на максимум. На двух последовательных итерациях значения целевой функции связаны соотношением:

где

Если задача невырожденная, то для любого шага  . Отсюда
. Отсюда  , т. е. значение целевой функции будет не хуже прежнего (монотонно возрастает). Аналогично, если задача решается на минимум, то, поскольку
, т. е. значение целевой функции будет не хуже прежнего (монотонно возрастает). Аналогично, если задача решается на минимум, то, поскольку  , на любом шаге значения целевой функции на двух последовательных итерациях будут связаны неравенством
, на любом шаге значения целевой функции на двух последовательных итерациях будут связаны неравенством 
 , т. е. целевая функция монотонно убывает. В этом и состоит монотонность симплексного метода.
, т. е. целевая функция монотонно убывает. В этом и состоит монотонность симплексного метода.
Конечность алгоритма следует из конечного числа опорных планов ЗЛП (их не больше  ).
).
Если ЗЛП вырожденная, то возможны случаи, когда  . В этом случае значение целевой функции не улучшится. Предположим, что процесс продолжается без остановки, порождая бесконечную последовательность опорных планов. Вследствие конечности множества опорных планов в этой последовательности некоторые планы должны повторяться. В силу равенства для них целевой функции они должны лежать в одной гиперплоскости и быть вершинами выпуклого многогранника. Поэтому должна встретиться цепочка (цикл)
. В этом случае значение целевой функции не улучшится. Предположим, что процесс продолжается без остановки, порождая бесконечную последовательность опорных планов. Вследствие конечности множества опорных планов в этой последовательности некоторые планы должны повторяться. В силу равенства для них целевой функции они должны лежать в одной гиперплоскости и быть вершинами выпуклого многогранника. Поэтому должна встретиться цепочка (цикл)  , в которой начальный и конечный планы совпадают, причем в силу монотонности метода
, в которой начальный и конечный планы совпадают, причем в силу монотонности метода

Процесс продолжится неограниченно, если несколько последовательных вырождении приведут к образованию цикла. Такое явление называется зацикливанием. Зацикливание возможно только для вырожденных задач. Теория и практика показывают, что зацикливание возникает при весьма маловероятном сочетании условий. Известно лишь несколько специально разработанных (очень сложных) примеров, в процессе решения которых возникает зацикливание. Точный алгоритм вывода из цикла достаточно сложен. В простейшем случае при появлении цикла следует изменить последовательность вычислений путем изменения выбора разрешающего столбца. Другое правило рекомендует изменить выбор разрешающей строки. Если в процессе симплексных преобразований появляется несколько минимальных симплексных отношений, то в качестве разрешающей выбирают ту строку, для которой будет наименьшим отношение элементов первого столбца к разрешающему. Если при этом снова оказывается несколько минимальных отношений, то составляются отношения элементов второго столбца к разрешающему, и так до тех пор, пока разрешающая строка не определится однозначно.
2.12. Понятие двойственности для симметричных задач линейного программирования
Рассмотрим понятие двойственности на примере задачи о рациональном использовании сырья.
Пусть на некотором предприятии решили рационально использовать отходы основного производства. В плановый период появились отходы m-видов в объемах 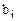 единиц (
единиц ( . Из этих отходов, учитывая специфику предприятия, можно наладить производство n-видов неосновной продукции.
. Из этих отходов, учитывая специфику предприятия, можно наладить производство n-видов неосновной продукции.
Обозначим через 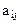 норму расходов сырья i-вида на единицу j-ой продукции.
норму расходов сырья i-вида на единицу j-ой продукции. 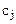 - цена единицы j- продукции. Неизвестные величины задачи:
- цена единицы j- продукции. Неизвестные величины задачи: 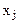 - объемы выпуска j-продукции, обеспечивающие предприятию максимальную выручку.
- объемы выпуска j-продукции, обеспечивающие предприятию максимальную выручку.
Математическая модель задачи:
 , (1)
, (1)
при ограничениях
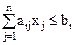 (
( ),
),
 , (
, ( ).
).
Предположим с самого начала, при изучении вопроса об использовании отходов основного производства на предприятии, появилась возможность реализации их некоторой организации. Необходимо установить цены на эти отходы. Обозначим цены через 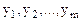 . Цены должны быть установлены исходя из двух основных условий: 1) общую стоимость сырья покупающая сторона стремится минимизировать; 2) предприятие согласно уступить свою продукции только по таким ценам, при которых оно получит за них выручку не меньшую той, что оно могло бы получить организовав собственное производство.
. Цены должны быть установлены исходя из двух основных условий: 1) общую стоимость сырья покупающая сторона стремится минимизировать; 2) предприятие согласно уступить свою продукции только по таким ценам, при которых оно получит за них выручку не меньшую той, что оно могло бы получить организовав собственное производство.
Математическая модель полученной задачи:
 (2)
(2)

Переменные  называются двойственными оценками (теневые цены).
называются двойственными оценками (теневые цены).
Задачи (1) и (2) называются парой взаимодвойственных задач. Так как они написаны в симметричной форме их называют парой взаимодвойственных симметричных задач.
 ,
при ,
при
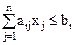 ( ( ), ),
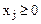 ( ( ) )
|  при
при
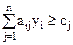 ( ( ) )
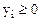 ( ( ) )
|
Сравнивая прямую и двойственную задачи можно установить следующие взаимосвязи:
1. Если прямая задача на максимум, то двойственная на минимум.
2. Коэффициенты 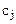 целевой функции прямой задачи являются свободными членами ограничений двойственной задачи.
целевой функции прямой задачи являются свободными членами ограничений двойственной задачи.
3. Свободные члены 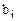 ограничений прямой задачи, являются коэффициентами целевой функции двойственной задачи.
ограничений прямой задачи, являются коэффициентами целевой функции двойственной задачи.
4. Матрицы ограничений прямой и двойственной задачи являются транспонируемыми друг к другу.
5. Если прямая задача на максимум то ее система ограничений представляется в неравенства типа  . Двойственная задача решается на минимум и знак ³.
. Двойственная задача решается на минимум и знак ³.
6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной равно числу переменных прямой.
7. Все переменные в обоих задачах не отрицательны.
Пример: Составить симметричную двойственную задачу:

при

Решение:
Исходная задача на максимум, значит двойственная – на минимум. Свободные члены системы ограничений исходной задачи равны 2 и 5. Значит коэффициенты в целевой функции двойственной задачи будут 2 и 5. Коэффициенты в целевой функции прямой задачи – 27, 10, 15, 28. Следовательно эти значения будут свободными членами в системе ограничений двойственной задачи. Таким образом, транспонируя матрицу А, получим:
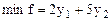
при

Блок 3
3.1. Несимметричные двойственные задачи
Пуст ЗЛП задана в каноническом виде:

при
 (
( ),
),
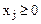 (
(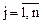 ).
).
Переведем данную задачу в симметричную форму:

Прямая задача на максимум, значит неравенства должны быть ≤. Умножим второе неравенство на (-1). Получим:

Составим двойственную задачу для полученной симметричной. Для этого введем двойственные переменные 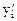 и
и 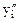 . Получим:
. Получим:

при ограничениях:

Преобразуем систему ограничений следующим образом:

Обозначим y разность  .
. 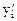 и
и 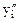 положительны, но их разность может быть как положительна, так и отрицательна.
положительны, но их разность может быть как положительна, так и отрицательна.
В результате получим двойственную задачу вида:

при

Подводя итоги вышеизложенному, опишем прямую и двойственную задачу для ЗЛП в общем случае:
 при
при
 ( ( ), ),
 ( ( ), ),
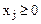 ( ( ), ),
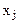 – любого знака ( – любого знака ( ). ).
|  при
при
 ( ( ), ),
 ( ( ), ),
 ( ( ), ),
 – любого знака ( – любого знака ( ). ).
|
Таким образом, двойственная задача со смешанными ограничениями составляется с соблюдением следующих дополнительных правил:
1. Если на переменную  прямой задачи наложено условие неотрицательности, то j-тое условие системы ограничений двойственной задачи в виде неравенств и наоборот.
прямой задачи наложено условие неотрицательности, то j-тое условие системы ограничений двойственной задачи в виде неравенств и наоборот.
2. Если на переменную  прямой задачи не наложено условие неотрицательности, то j-тое ограничение двойственной задачи записывается в виде строго равенства.
прямой задачи не наложено условие неотрицательности, то j-тое ограничение двойственной задачи записывается в виде строго равенства.
3. Если в прямой задачи имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагается условие неотрицительности.
Задача двойственная двойственной будет совпадать с исходной. Поэтому безразлично которую задачу можно принять за прямую, которую за двойственную. Следует говорить о паре взаимно двойственных задач.
Рассмотри пару двойственных задач.
Теорема 1: (об основном неравенстве двойственности) Для любых допустимых планов X=  и Y=
и Y= 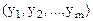 прямой и двойственной задачи линейного программирования справедливо неравенство:
прямой и двойственной задачи линейного программирования справедливо неравенство:
 .
.
Экономическое содержание основного неравенства двойственности состоит в том, что для любого допустимого плана производства Х и любого вектора оценок ресурсов Y общая созданная стоимость не превосходит суммарной оценки ресурсов.
Теорема 2: (критерий оптимальности Канторовича) Если для некоторых допустимых планов  и
и 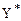 пары двойственных задач выполняется равенство z(
пары двойственных задач выполняется равенство z( )=f(
)=f(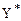 ), то
), то  и
и 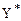 являются оптимальными планами соответствующих задач.
являются оптимальными планами соответствующих задач.
Экономическое содержание теоремы состоит в том, что план производства Х и вектор оценок ресурсов Y является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
Теорема 3: (малая теорема двойственности) Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
Теорема 4: Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: z( )=f(
)=f(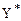 ). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых планов, то система ограничений другой – противоречива.
). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых планов, то система ограничений другой – противоречива.
Между переменными двойственных задач можно установить соответствие, сопоставляя свободным переменным одной задачи базисные переменные другой. Опорному оптимальному плану исходной задачи соответствует опорный оптимальный план двойственной, который оказывается записанным с противоположными знаками в индексной строке последней симплексной таблицы.
Пример 1: Решить исходную задачу линейного программирования, исходя из решения двойственной:

при 
Решение.
Преобразуем систему ограничений следующим образом:

Составим двойственную задачу для данной:

при 
Решим полученную задачу симплексным методом. Преобразуем систему ограничений следующим образом:

Для полученной М-задачи составим симплексную таблицу.
| БП | СБ | А | 
| 
| 
| 
| 
| 
| 
| 
| 
|
| -4 | -6 | M | M | M | |||||||
| M | -1 | -1 | -1 | |||||||
| M | -1 | -1 | ||||||||

| M | -1 | |||||||||
| M | -1 | -1 | -1 | ||||||||
| св. член | -8 | ||||||||||

| -1 | -1 | -1 | ||||||||
| M | -1 | |||||||||

| M | -1 | |||||||||
| M | -1 | -1 | |||||||||
| св. член | -4 | -2 | -8 | ||||||||

| -1 | -1/2 | -1/2 | ||||||||

| -4 | 1/2 | -1/2 | ||||||||

| M | 1/2 | 1/2 | -1 | |||||||
| M | 1/2 | 1/2 | -1 | ||||||||
| св. член | -2 | -6 | |||||||||

| -1 | ||||||||||

| -4 | 1/2 | -1/2 | ||||||||

| -6 | 1/2 | 1/2 | -1 | |||||||
| -5 | -1 | -2 |
Полученный план оптимальный.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 2421; Нарушение авторских прав?; Мы поможем в написании вашей работы!