
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные виды записи задач линейного программирования 1 страница
|
|
|
|
Определение: Общей задачей линейного программирования называют задачу:

при ограничениях
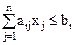 (
( );
);
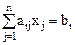 (
( );
);
 (
(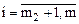 );
);
 (
(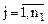 );
);
 - произвольные (
- произвольные ( ),
),
где  ,
,  ,
,  - заданные действительные числа.
- заданные действительные числа.
Определение: Симметричной формой записи задачи линейного программирования называют задачу:

при ограничениях
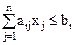 (
( );
);
 (
( );
);
или задачу
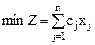
при ограничениях
 (
( );
);
 (
( ).
).
Определение: Канонической формой записи задачи линейного программирования называют задачу:

при ограничениях
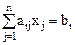 (
( );
);
 (
( ).
).
Рассмотрим еще два вида записи- матричную и векторную.
Введем обозначения:  ,
,
 ,
,  ,
, 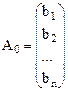 ,
,
где С – матрица-строка; А – матрица системы уравнений, Х – матрица-столбец переменных, 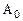 - матрица-столбец свободных членов.
- матрица-столбец свободных членов.
Каноническая форма записи примет вид:
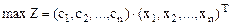
или
max Z=CX
при ограничениях
 ,
, 
или
 ,
,  .
.
Запишем задачу линейного программирования в векторной форме:
 ,
, 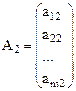 ,...,
,...,  ,...,
,...,  .
.
Тогда задача линейного программирования в канонической форме записи имеет вид:

при ограничениях
 ,
,  ,
,
где 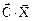 - скалярное произведение векторов
- скалярное произведение векторов 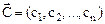 и
и  .
.
1.10. Способы преобразования
При необходимости задачу минимизации можно заменить задачей максимизации и наоборот. Для функции одной переменной это утверждение очевидно. В самом деле, если 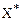 - точка максимума функции y=f(x), то для функции y=-f(x) она является точкой максимума, так как графики функций f(x) и –f(x) симметричны относительно оси абсцисс (рис. 1).
- точка максимума функции y=f(x), то для функции y=-f(x) она является точкой максимума, так как графики функций f(x) и –f(x) симметричны относительно оси абсцисс (рис. 1).
Итак, min f(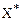 ) = max (-f(
) = max (-f(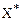 )).
)).
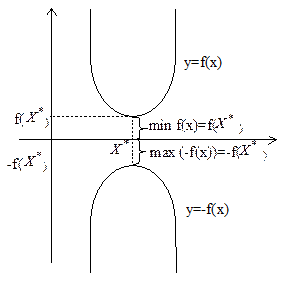
Рис. 1. Графики функций y=f(x) и y=-f(x).
То же самое имеет место в случае функции n переменных:
 .
.
1.11. Переход к канонической форме
Из примеров задач линейного программирования следует, что большинство ограничений задается неравенствами. Основные же методы решения задач линейного программирования применяются лишь к задачам, записанным в канонической форме. Поэтому приходится переходить от любой формы записи задач линейного программирования к ее каноническому виду, причем, нужно быть уверенным, что эти формы эквивалентны.
Пусть исходная задача линейного программирования имеет вид:

при ограничениях:
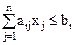 (
( ); (1)
); (1)
 (
(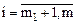 ); (2)
); (2)
 (
( ).
).
Преобразуем ее к каноническому виду. Введем m дополнительных неотрицательных переменных  (
( ). Для того чтобы неравенства типа £ преобразовать в равенства, к их левым частям прибавим дополнительные переменные
). Для того чтобы неравенства типа £ преобразовать в равенства, к их левым частям прибавим дополнительные переменные  (
( ) после чего система неравенств (1) примет вид:
) после чего система неравенств (1) примет вид:
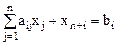 (
( ) (3).
) (3).
Для того чтобы неравенства типа ³ (2) преобразовать в равенства, из их левых частей вычтем дополнительные переменные  (
(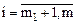 ). Получим:
). Получим:
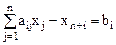 (
(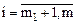 ) (4).
) (4).
Систему уравнений (3) и (4) с условием неотрицательности дополнительных переменных называют эквивалентной системе неравенств (1) и (2) соответственно.
Дополнительные переменные  (
( ) в целевую функцию вводятся с коэффициентами, равными 0.
) в целевую функцию вводятся с коэффициентами, равными 0.
Получим задачу:
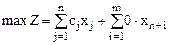 ,
,
при ограничениях:
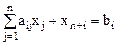 (
( );
);
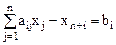 (
(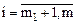 );
);
 (
( );
);  (
( ).
).
Теорема 11.1 (о переходе к канонической форме записи) Каждому допустимому решению  задачи
задачи

Соответствует вполне определенное допустимое решение  задачи
задачи

И наоборот, каждому решению  задачи (6) соответствует допустимое решение
задачи (6) соответствует допустимое решение  задачи (5).
задачи (5).
Пример 1. Привести к канонической форме записи задачу:
Найти:

при ограничениях:
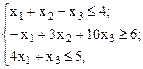
 ,
,  ,
,  .
.
Решение.
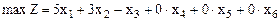
при ограничениях
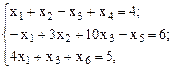
 ,
,  ,
,  ,
, 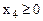 ,
,  ,
,  .
.
Пример 2. Привести к канонической форме записи задачу:
Найти:
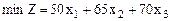
при ограничениях:
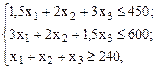
 ,
,  ,
,  .
.
Решение.
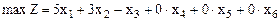
при ограничениях
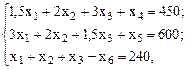

 ,
,  ,
,  ,
, 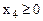 ,
,  ,
,  .
.
Отметим экономический смысл дополнительных переменных. Они в каждой задаче прямо связаны с ее экономическим содержанием. Например, для задачи о наилучшем использовании ресурсов:
 (
( ),
),
т.е. дополнительная переменная указывает величину неиспользованного ресурса. Для задачи о смесях:
 (
( ),
),
т.е. дополнительная переменная показывает потребление соответственного питательного вещества в оптимальном плане сверх нормы.
В ряде производственно-экономических ситуаций не на все переменные налагаются условия неотрицательности. В подобных ситуациях, даже если ограничения представлены в виде равенств, задача не будет канонической. Для представления такой задачи в каноническом виде каждую из переменных 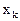 , на которые не наложено условие неотрицательности, заменим разностью двух неотрицательных переменных
, на которые не наложено условие неотрицательности, заменим разностью двух неотрицательных переменных  и
и  , т.е.
, т.е.
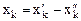 ,
,
где  ³ 0 и
³ 0 и  ³ 0 (этим приемом мы воспользуемся при изучении двойственных задач).
³ 0 (этим приемом мы воспользуемся при изучении двойственных задач).
1.12. Переход к симметричной форме записи
Переход к симметричной форме записи можно осуществить двумя способами.
Первый способ. Пусть в общей задаче линейного программирования имеются ограничения равенства
 (
( );
);
Каждое ограничение-равенство эквивалентно системе неравенств:

Неравенство вида ³ умножением обеих частей на –1 превращается в неравенство вида £, и наоборот.
Второй способ. Рассмотрим задачу линейного программирования в каноническом виде

при ограничениях
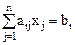 (
( );
);
 (
( ).
).
Приведем ее к симметричной форме. Пусть ранг системы ограничений равен r.
Определение: Рангом системы уравнений называют количество линейно независимых уравнений.
Если r<n, то система будет иметь бесконечное множество решений. Не ограничивая общности, можно считать, что в матрице системы линейно независимы первые r столбцов. Методом Гаусса систему преобразуем к виду:
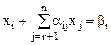 (i=
(i=  ). (1)
). (1)
Переменные  называют базисными,
называют базисными,  - свободными.
- свободными.
Отсюда:
 (i=
(i=  ).
).
Так как все переменные  (
( ), то можно составить следующие неравенства:
), то можно составить следующие неравенства:
 , (i=
, (i=  ).
).
Перенесем свободные члены неравенств в левую часть:
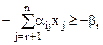 , (i=
, (i=  ).
).
Целевая функция в исходной задаче исследуется на max, следовательно, в системе ограничений все неравенства должны быть « ». Для того чтобы полученные неравенства привести к требуемому виду, умножим обе части его на –1.
». Для того чтобы полученные неравенства привести к требуемому виду, умножим обе части его на –1.
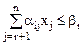 , (i=
, (i=  ).
).
Выразим целевую функцию через свободные переменные. Для этого подставим значения  из равенств (1) в формулу:
из равенств (1) в формулу:

 Обозначим:
Обозначим:
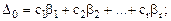

…………………………………….

Подставим полученные значения в целевую функцию. Получим:
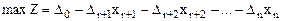
Следовательно, после всех преобразований мы получим следующую задачу линейного программирования:
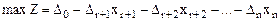
при
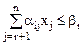 , (i=
, (i=  ).
).
 (
( ).
).
Полученная задача является симметричной.
К данному способу преобразований мы вернемся при изучении симплексного метода решения задач линейного программирования.
Блок 2.
2.1. Геометрическая интерпретация задачи линейного программирования
Одним из возможных вариантов решения задачи линейного программирования является графический метод. Это специальный метод, не предназначенный для решения любых задач. Его можно использовать при решении ЗЛП, в котором всего две переменные. Это условие накладывается потому, что точная графическая интерпретация ЗЛП, позволяющая найти решение, возможна лишь на плоскости.
Пусть задача линейного программирования имеет вид:

при
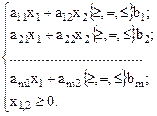
Для того, чтобы интерпретировать задачу линейного программирования, заданную подобным образом, необходимо интерпретировать систему ограничений и целевую функцию.
Интерпретируем систему ограничений. Каждое неравенство системы ограничений графически представляет собой полуплоскость, пересечение полуплоскостей дает часть плоскости, представляющую собой выпуклый многоугольник, может быть неограниченный с одной из сторон.
Примеры возможных расположений многоугольников:
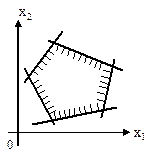

Рис. 2. Рис. 3.


Рис. 4. Рис. 5.


Рис. 6. Рис. 7.
Следовательно, область допустимых решений задачи линейного программирования может быть: выпуклый многоугольник, неограниченная, выпуклая область, единственная точка, прямая линия, отрезок, пустое множество.
Интерпретируем целевую функцию. Графическая интерпретация целевой функции представляет собой систему параллельных линий. Каждую из них мы назовем линией уровня.
2.2. Решение задач линейного программирования графическим методом
Решение задачи линейного программирования графическим методом производится по следующему алгоритму:
1. Интерпретируется система ограничений. Строится область допустимых решений.
2. Строится произвольная линия уровня.
Замечание: При решении ЗЛП графическим методом удобнее всего строить линию уровня при Z=0.
3. Выбирается направление перемещения линии уровня.
Замечание1: Направление перемещения линии уровня выбирается с учетом направления наибольшего изменения функции. Это направление определяется с помощью градиента:
grad Z =  =(
=( ,
,  )
)
Если решается задача на max, то выбирается направление вектора градиента (направление вектора  ). В противном случае – направление антиградиента (вектора -
). В противном случае – направление антиградиента (вектора -  ).
).
Замечание 2: С помощью вектора  можно построить линию уровня. Она строится перпендикулярно градиенту, через точку (0,0).
можно построить линию уровня. Она строится перпендикулярно градиенту, через точку (0,0).
4. Перемещается линия уровня, до тех пор, пока не найдено решение ЗЛП.
Замечание 1: При решении ЗЛП возможны следующие случаи:


Рис. 8 Рис. 9.


Рис. 10 Рис. 11
На рис. 8 показан случай, когда минимум и максимум целевой функции найдены и находятся соответственно в точках max и min. Во втором случае (рис. 9) минимум целевой функции существует. Однако область допустимых решений не ограничена сверху, следовательно, максимума у целевой функции нет. В третьем случае (рис. 10) нет ни минимума, ни максимума функции. На рис.11 ЗЛП имеет бесконечно много решений.
Пример1: Решить ЗЛП графическим методом. Найти:

при

Решение.
Найдем градиент: 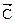 (2;-3).
(2;-3).
Построим область допустимых значений. Для этого построим прямые, соответственные ограничениям:



| 1: | A | B | 2: | A | B | 3: | A | B | ||
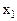
| -6 |  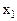
| 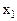
| |||||||
| 
| 
|

| y | |||||||||||||||

| 
| ||||||||||||||
 2 2
| 
| ||||||||||||||
| |||||||||||||||

| |||||||||||||||
| x | |||||||||||||||
| C | 
| ||||||||||||||

| |||||||||||||||
Решение находится, исходя из решения системы:
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 1076; Нарушение авторских прав?; Мы поможем в написании вашей работы!