Блок 1

Блок 4

Блок 3

Блок 2

Блок 1

1. Предмет и задачи исследования операций.

2. Основные понятия и принципы исследования операций.

3. Математические модели операций.

4. Понятие линейного программирования.

5. Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов.

6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий.

7. Примеры экономических задач линейного программирования. Задача о смесях.

8. Примеры экономических задач линейного программирования. Транспортная задача.

9. Основные виды записи задач линейного программирования.

10. Способы преобразования.

11. Переход к канонической форме.

12. Переход к симметричной форме записи.

1. Геометрическая интерпретация задачи линейного программирования.

2. Решение задач линейного программирования графическим методом.

3. Свойства решений задачи линейного программирования.

4. Общая идея симплексного метода.

5. Построение начального опорного плана при решении задач линейного программирования симплексным методом.

6. Признак оптимальности опорного плана. Симплексные таблицы.

7. Переход к нехудшему опорному плану.

8. Симплексные преобразования.

9. Альтернативный оптимум (признак бесконечности множества опорных планов).

10. Признак неограниченности целевой функции.

11. Понятие о вырождении. Монотонность и конечность симплексного метода. Зацикливание.

12. Понятие двойственности для симметричных задач линейного программирования.

1. Несимметричные двойственные задачи.

2. Открытая и закрытая модели транспортной задачи.

3. Построение начального опорного плана. Правило "Северо-западного угла".

4. Построение начального опорного плана. Правило минимального элемент.

5. Построение начального опорного плана. Метод Фогеля.

6. Метод потенциалов.

7. Решение транспортных задач с ограничениями по пропускной способности.

8. Примеры задач дискретного программирования. Задача о контейнерных перевозках. Задача о назначении.

9. Сущность методов дискретной оптимизации.

10. Задача выпуклого программирования.

11. Метод множителей Лагранжа.

12. Градиентные методы.

1. Метод штрафных и барьерных функций.

2. Динамическое программирование. Основные понятия. Сущность методов решения.

3. Стохастическое программирование. Основные понятия.

4. Матричные игры с нулевой суммой.

5. Чистые и смешанные стратегии.

6. Свойства чистых и смешанных стратегий.

7. Приведение матричной игры к ЗЛП

8. Задачи теории массового обслуживания. Классификация систем массового обслуживания.

9. Потоки событий.

10. Схема гибели и размножения.

11. Формула Литтла.

12. Простейшие системы массового обслуживания.

1.1. Предмет и задачи исследования операций

Современное состояние науки и техники, в частности, развитие компьютерных средств расчета и математического обоснования теорий позволило значительно упростить решение многих проблем, поставленных перед различными отраслями науки. Многие из проблем сводятся к решению вопроса об оптимизации производства, оптимальному управлению процессами.

Потребности практики вызвали к жизни специальные научные методы, которые удобно объединять под названием «исследование операций».

Определение: Под исследованием операций будем понимать применение математических, количественных методов для обоснование решений во всех областях целенаправленной человеческой деятельности.

Пусть предпринимается какое-то мероприятие, направленное к достижению определенной цели. У лица (или группы лиц), организующего мероприятие, всегда имеется какая-то свобода выбора: оно может быть организовано тем или иным способом. Решение и есть какой-то выбор из ряда возможностей, имеющихся у организатора.

Необходимость принятия решений и проверки выдвинутой гипотезы решения математически подтверждают следующие примеры:

Задача 1. О наилучшем использовании ресурсов.

На предприятии выпускается несколько видов продукции. Для их изготовления используются некоторые ресурсы (в том числе человеческие, энергетические и т.д.). Необходимо рассчитать, каким образом спланировать работу предприятия, чтобы затраты ресурсов были минимальны, а прибыль – максимальной.

Задача 2. О смесях.

Необходимо подготовить смесь, обладающую определенными свойствами. Для этого можно использовать некоторые "продукты" (для расчета диет – продукты питания, для кормовых смесей – продукты питания для животных, для технических смесей – сплавы, жидкости технического назначения). задача заключается в выборе оптимального количества продуктов (по цене) для получения оптимального количества смеси.

Задача 3. Транспортная задача.

Существует сеть предприятий, выпускающих однотипную продукцию одного качества и сеть потребителей этой продукции. Потребители и поставщики связаны путями сообщений (автодороги, железнодорожные линии, авиационные линии). Определены тарифы перевозок. Необходимо рассчитать оптимальный план перевозок продукции, чтобы затраты при перевозке были минимальны, запросы всех потребителей удовлетворены, а у поставщиков весь товар вывезен.

В каждом из приведенных примеров речь идет о каком-то мероприятии, преследующем определенную цель. Заданы некоторые условия, характеризующие обстановку (в частности, средства, которыми можно распоряжаться). В рамках этих условий требуется принять такое решение, чтобы задуманное мероприятие было в некотором смысле более выгодным.

В соответствии с этими общими чертами вырабатываются и общие приемы решения подобных задач, в совокупности составляющие методологическую схему и аппарат исследования операций.

В настоящее время большое распространение принимают автоматизированные системы управления (АСУ), основанные на использовании компьютерной техники. Создание АСУ невозможно без предварительного обследования управляемого процесса методами математического моделирования. С ростом масштабов и сложности мероприятий математические методы обоснования решений приобретают все большую роль.

1.2. Основные понятия и принципы исследования операций

Определение: Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели.

Операция есть всегда управляемое мероприятие, т.е. от расчетов зависит, каким способом выбрать параметры, характеризующие ее организацию. «Организация» здесь понимается в широком смысле слова, включая набор технических средств, применяемых в операции.

Определение: Всякий определенный выбор зависящий от решающих параметров называется решением.

Определение: Оптимальными называются решения, по тем или иным причинам предпочтительные перед другими.

Цель исследования операций – предварительное количественное обоснование оптимальных решений.

Иногда в результате исследования удается указать одно-единственное строго определенное решение, гораздо чаще – выделить область практически равноценных оптимальных решений, в пределах которой может быть сделан конечный выбор.

Само принятие решений выходит за рамки исследования операций и относится к компетенции ответственного лица, чаще – группы лиц, которым представляется право окончательного выбора и на которых возложена ответственность за этот выбор.

Определение: Параметры, совокупность которых образует решение, называются элементами решения.

В качестве элементов решения могут фигурировать различные числа, векторы, функции, физические признаки и т.д. Для упрощения всю совокупность элементов решения будем обозначать х.

Кроме элементов решения в любой задачи исследования операций имеются еще и заданные условия, которые фиксированы в условии задачи и нарушены быть не могут. В частности, к таким условиям относятся средства (материальные, технические, людские), которыми можно распоряжаться, и иные ограничения, налагаемые на решение. В своей совокупности они образуют так называемое «множество возможных решений». Обозначим это множество Х, а тот факт, что решение х принадлежит этому множеству, будем записывать: хÎХ.

Чтобы сравнивать между собой по эффективности разные решения, нужно иметь какой-то количественный критерий, так называемый показатель эффективности (целевая функция). Этот показатель выбирается так, чтобы он отражал целевую направленность операции. Лучшим будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели. Чтобы выбрать показатель эффективности Z, нужно прежде всего определить, к чему должно привести решение задачи. Выбирая решение, предпочтение отдается такому, которое обращает показатель эффективности Z в максимум или в минимум. Например, доход от операции хотелось бы обратить в максимум; если же показателем эффективности являются затраты, их желательно обратить в минимум.

Очень часто выполнение операции сопровождается действием случайных факторов: «капризов» природы, колебания спроса и предложения, отказы технических устройств и т.д. В таких случаях обычно в качестве показателя эффективности берется не сама величина, которую хотелось бы максимизировать (минимизировать), а среднее значение (математическое ожидание).

Задача выбора показателя эффективности решается для каждой проблемы индивидуально.

Задача 1. О наилучшем использовании ресурсов.

Задача операции – произвести максимальное количество товаров. Показатель эффективности Z – прибыль от продажи товаров при минимальных затратах на ресурсы (max Z).

Задача 2. О смесях.

Естественный показатель эффективности, подсказанный формулировкой задачи, - это цена необходимых для смеси продуктов при условии необходимости сохранения заданных свойств смеси(min Z).

Задача 3. Транспортная задача.

Задача операции – обеспечить снабжение товарами потребителей при минимальных расходах на перевозки. Показатель эффективности Z – суммарные расходы на перевозки товаров за единицу времени (min Z).

1.3. Математические модели операций

Для применения количественных методов исследования в любой области всегда требуется какая-то математическая модель. При построении модели реальное явление (в нашем случае – операция) неизбежно упрощается, схематизируется, и эта схема описывается с помощью того или иного математического аппарата.

Общих способов построения математических моделей не существует. В каждом конкретном случае модель выбирается исходя из вида операции, ее целевой направленности, с учетом задачи исследования (какие параметры требуется определить и влияние каких факторов отразить). Необходимо также в каждом конкретном случае соразмерять точность и подробность модели:

а) с той точностью, с которой нужно знать решение;

б) с той информацией, которой мы располагаем или можем приобрести.

Если исходные данные, нужные для расчетов, известны неточно, то, очевидно, нет смысла входить в тонкости, строить очень подробную модель и тратить время (свое и машинное) на тонкую и точную оптимизацию решения. К сожалению, этим принципом часто пренебрегают и выбирают для описания явлений слишком подробные модели.

Математическая модель должна отражать важнейшие черты явления, все существенные факторы, от которых зависит успех операции. Вместе с тем модель должна быть по возможности более простой. Две опасности всегда подстерегают составителя модели: первая – увязнуть в подробностях и вторая – слишком огрубить явление. Создание математической модели – самая важная и ответственная часть исследования, требующая глубокого знания не столько математики, сколько существа моделируемых явлений.

Многие задачи, с которыми приходится иметь дело в повседневной практике, являются многовариантными. Среди множества вариантов в условиях рыночных отношений приходится отыскивать наилучшие в некотором смысле при ограничениях, налагаемых на природные, экономические и технологические возможности. До недавнего времени большинство таких задач решалось исходя из здравого смысла и опыта лиц, принимающих решения, или просто «на глаз». При таком подходе не было и не могло быть никакой уверенности, что найденный вариант – наилучший. При современных масштабах производства даже незначительные ошибки оборачивались громадными потерями. В связи с этим возникла необходимость применять для анализа и синтеза экономических ситуаций и систем математические методы и современную вычислительную технику. Такие методы объединяются под общим названием – математическое программирование.

Определение: Математическое программирование – область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Определение: Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием оптимальности.

Экономические возможности формализуются в виде системы ограничений. Все это составляет математическую модель.

Определение: Математическая модель задачи – это отражение оригинала в виде функций, уравнений, неравенств, цифр и т.д.

Математическая модель задачи математического программирования включает:

· совокупность неизвестных величин

,

действуя на которые систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, стратегией, поведением и др.);

· целевую функцию (функцию цели, показатель эффективности, критерий оптимальности, функционал задачи и др.). Целевая функция позволяет выбрать наилучший вариант из множества возможных. Наилучший вариант доставляет целевой функции экстремальное значение;

· условия (или систему ограничений), налагаемые на неизвестные величины. Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов. Ограниченными являются не только материальные, финансовые и трудовые ресурсы, но и таковыми могут быть возможности технического, технологического и, вообще, научного потенциала. Математически ограничения выражаются в виде уравнений и неравенств. Их совокупность образует область допустимых решений (область экономических возможностей). Объединение всех условий (ограничений), налагаемых на известные (искомые) величины задачи, обозначим: W (хÎW). При таких обозначениях модель задачи математического программирования примет вид: max (min) Z = z(x), xÎW, или найти extremum Z = z(x), xÎW.

В развернутом виде: найти план , доставляющий экстремальное значение целевой функции z, т.е.

max (min) Z = z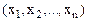

при ограничениях

Замечание: надпись «» означает «i изменяется от 1 до m».

Из экономических или физических соображений на план задачи или некоторые его компоненты (координаты) накладываются условия не отрицательности:

,

иногда – целочисленности.

Определение: План Х, удовлетворяющий системе ограничений задачи, называется допустимым (ХÎW).

Определение: Допустимый план, доставляющий функции цели экстремальное значение, называется оптимальным.

Оптимальный план будем обозначать 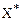, экстремальное значение функции цели – z(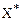)= . Оптимальное решение, вообще говоря, не обязательно единственное, возможны случаи, когда оно не существует, имеется конечное или бесконечное множество оптимальных решений.

1.4. Понятие линейного программирования

Определение: Линейное программирование – это раздел математического, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные.

По типу решаемых задач его методы делятся на универсальные и специальные. С помощью универсальных методов могут быть решены любые задачи линейного программирования. Специальные же методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функций во внутренней точке области допустимых значений. Отсюда – необходимость разработки новых методов.

Математическая модель ЗЛП:

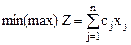
при

1.5. Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов

Пусть некоторая производственная единица (цех, завод, объединение и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексами j . Предприятие при производстве этих видов продукции должно ограничиваться имеющими видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Пусть их число равно m, припишем им индекс i 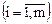. Они ограничены, и их количества равны соответственно условных единиц. Таким образом, - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчислимая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д.

Примем в качестве такой меры, например, цену реализации (), т.е. 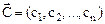- вектор цен. Известны также технологические коэффициенты , которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов || || называют технологической матрицей и обозначают А:

.

Обозначим через Х= 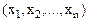- план производства, показывающий какие виды товаров нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.

Так как - цена реализации единицы j-той продукции, цена реализации единиц будет равна , а общий объем реализации:

.

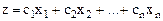Это выражение – целевая функция, которую нужно максимизировать.

Так как - расход i-го ресурса на производство единиц j-той продукции, то, просуммировав расход i-го ресурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить () единиц:

Чтобы искомый план Х= 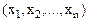был реален, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объемы выпуска продукции:

, ().

Таким образом, модель задачи о наилучшем использовании ресурсов имеет вид:

Найти:

,

при ограничениях

(),

, ().

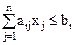Т.к. переменные входят в функцию Z(X) и систему ограничений только в первой степени, а показатели , , являются постоянными в планируемый период, то задача является задачей линейного программирования.

1.6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий

В задаче о наилучшем использовании ресурсов определяется оптимальный план выпуска продукции. Пусть при производстве какого-то общественно необходимого продукта используется n технологий. При этом требуется m видов ресурсов, заданных объемами (). Эффективности, т.е. количество конечной продукции (в рублях), производимой в единицу времени по j-той () технологии, обозначим через . Пусть, далее, - расход i-го ресурса в единицу времени по j-той технологии. В качестве неизвестной величины примем интенсивность использования j-той технологии, т.е. время, в течении которого продукция производится по j-той технологии. Пренебрегая временем переналадок, необходимыми для перехода от одной технологии к другой, получим следующую математическую модель задачи: найти план интенсивностей использования технологий Х= 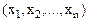, обеспечивающий максимум выпуска в стоимостном выражении:

,

при ограничениях на лимитируемые ресурсы

(),

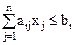и условия неотрицательности

, ().

1.7. Примеры экономических задач линейного программирования. Задача о смесях

В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходным материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе относят задачи о выборе диеты, составления кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности и т.д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.

Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете. Имеются пищевые продукты, известные под номерами 1, 2, 3,..., j,..., n. Они содержат различные питательные вещества, обозначаемые номерами 1, 2, 3,..., i,..., m (углеводы, белки, жиры, витамины, микроэлементы и др.). Единица j-го продукта содержит единиц i-го питательного вещества. Для нормальной жизнедеятельности в заданный промежуток времени нужно потреблять не менее единиц i-го питательного вещества. Обозначим через стоимость единицы продукции j-го вида. Требуется выбрать рацион минимальной стоимости, содержащие необходимые количества питательных веществ. План задач – это количества продуктов каждого вида, обеспечивающие необходимое количество питательных веществ при минимальных затратах на исходные продукты.

Математическая модель задачи:

Найти:

,

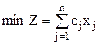при ограничениях

(),

, ().

1.8. Примеры экономических задач линейного программирования. Транспортная задача

Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям, при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем, потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. От схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.

Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено () единиц однородного продукта. Этот продукт нужно доставить n потребителям, где потребность составляет () единиц. Причем

.

Известны величины 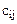- затраты на перевозку единицы продукта из i-го пункта производства в j-тый пункт потребления. Обозначим через количество продукта, перевозимое из i-го пункта производства в j-тый пункт потребления. Матрица С=|| 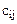|| называется матрицей тарифов

Матрица Х=|| || - матрицей перевозок:

С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи:

			...
			... ...
			... ...
...	... ...	... ...	... ...	... ...
			... ...

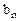
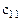
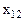
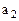
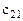
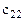
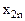
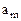
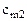
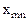
Математическая модель транспортной задачи: целевая функция, описывающая транспортные затраты,

,

минимизируется при ограничениях на возможности поставщиков: весь продукт из пункта производства должен быть вывезен:

();

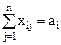на спрос потребителей, который должен быть удовлетворен:

();

при условии неотрицательности переменных, исключающем обратные перевозки

(, ).

Дата добавления: 2014-11-18