
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основы работы в зале
|
|
|
|
3)
2)
1)
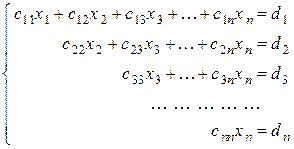 , (4.7)
, (4.7)
где 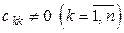 и
и 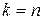 .
.
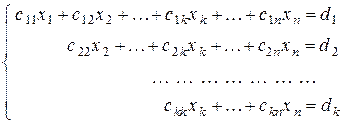 , (4.8)
, (4.8)
где  и
и 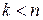 .
.
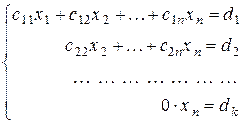 , (4.9)
, (4.9)
где 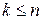 .
.
Запись системы, полученной после преобразований, называют ступенчатой (в частности, при 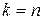 - треугольной).
- треугольной).
Система (4.7) имеет единственное решение. Из последнего уравнения 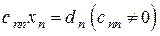 находим
находим 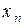 :
: 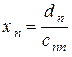 . Из предпоследнего уравнения находим
. Из предпоследнего уравнения находим 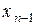 , затем из третьего от конца -
, затем из третьего от конца - 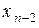 . Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные. Процесс преобразования системы (4.5) к одному из видов (4.7), (4.8) или (4.9) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (4.7) с целью получения значений неизвестных – обратным ходом.
. Двигаясь, таким образом, снизу вверх, найдем значения всех неизвестные. Процесс преобразования системы (4.5) к одному из видов (4.7), (4.8) или (4.9) называют прямым ходом метода Гаусса, а описанную только что процедуру движения снизу вверх по уравнениям системы (4.7) с целью получения значений неизвестных – обратным ходом.
Система (4.8) имеет бесчисленное множество решений. Из последнего уравнения можно выразить одно из неизвестных (например, 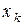 ) через остальные
) через остальные 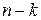 неизвестных (
неизвестных (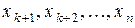 ), входящих в это уравнение. Полученное значение
), входящих в это уравнение. Полученное значение 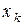 подставляем в последнее уравнение и находим выражение для
подставляем в последнее уравнение и находим выражение для 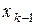 через эти неизвестные и т.д. И, наконец, выражаем
через эти неизвестные и т.д. И, наконец, выражаем 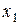 через
через 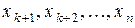 . В результате система (4.8.) будет приведена к виду
. В результате система (4.8.) будет приведена к виду
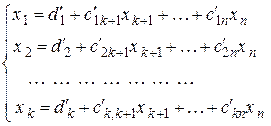 . (4.10)
. (4.10)
Полученная система представляет собой общее решение исходной системы. Неизвестные 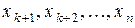 , стоящие в правой части равенств, называются свободными, а
, стоящие в правой части равенств, называются свободными, а 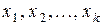 - базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (4.10) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании.
- базисными. Свободным неизвестным можно придавать любые числовые значения и по формулам (4.10) находить соответствующие значения базисных неизвестных. Каждый раз будет получаться определенное частное решение исходной системы. Заметим, что частное решение, получаемое из общего при нулевых значениях свободных неизвестных, называются базисным решением системы, которое играет исключительную роль в математическом программировании.
Система (4.9) не имеет решений, так как эта система несовместна, т.е. никакие значения неизвестных не могут удовлетворять ее последнему уравнению.
Итак, метод последовательного исключения неизвестных применим к любой системе линейных уравнений. Решая систему этим методом, преобразования можно совершать не над самими уравнениями, а над расширенной матрицей.
Пример 4.3. Решить СЛУ методом Гаусса: 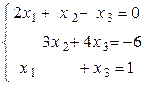 .
.
Решение. Составляем расширенную матрицу:
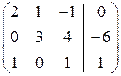 .
.
Сначала поменяем местами первую и третью строки, получаем:
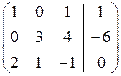 .
.
Поскольку во второй строке первый элемент равен нулю, то элементы второй строки не изменяем. Умножаем элементы первой строки на 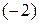 и складываем с соответствующими элементами третьей строки:
и складываем с соответствующими элементами третьей строки:
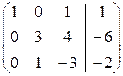 .
.
Теперь поменяем местами вторую и третью строки:
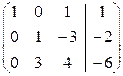 .
.
Умножаем элементы второй строки на 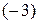 и складываем с соответствующими элементами третьей строки, получаем:
и складываем с соответствующими элементами третьей строки, получаем:
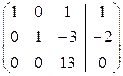 .
.
По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
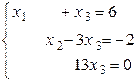 .
.
Из последнего уравнения находим 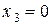 , из второго –
, из второго – 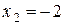 и из первого –
и из первого – 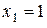 . Итак, исходная система имеет единственное решение
. Итак, исходная система имеет единственное решение 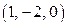 .
.
,
Пример 4.4. Решить систему уравнений
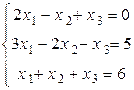 .
.
Решение. Составляем расширенную матрицу:
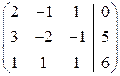 .
.
Сначала поменяем местами первую и третью строки, чтобы первый элемент (для удобства) был равен 1. Этот элемент будет разрешающим.
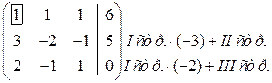 ~
~ 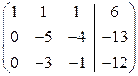 ~
~
[вторую и третью строки умножим на (-1)]
~ 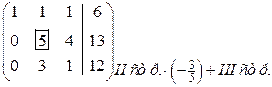 ~
~ 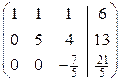 .
.
По коэффициентам последней матрицы составляем систему, равносильную исходной системе:
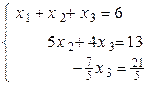 .
.
Из последнего уравнения находим 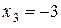 , из второго –
, из второго – 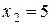 и из первого –
и из первого – 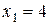 . Итак, исходная система имеет единственное решение
. Итак, исходная система имеет единственное решение 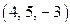 .
.
,
Пример 4.5. Решить систему уравнений
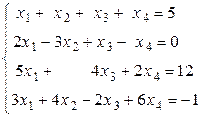 .
.
Решение. Составляем расширенную матрицу и преобразуем ее:
 ~
~ 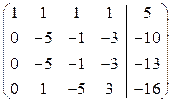 ~
~ 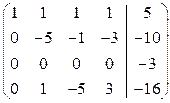 .
.
Система несовместна, так как последняя матрица содержит строку, соответствующую уравнению, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля.
,
Пример 4.6. Решить систему уравнений
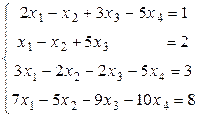 .
.
Решение. Составляем расширенную матрицу и преобразуем ее:
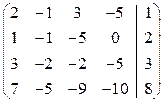 ~
~ 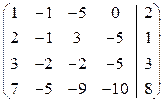 ~
~ 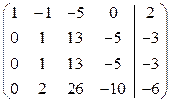 ~
~
~ 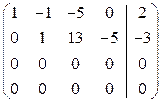 .
.
Исходная система свелась к ступенчатой:
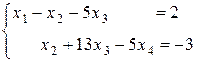 .
.
Из последнего уравнения за базисную неизвестную выберем, например, 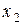 и выра-зим через свободные неизвестные
и выра-зим через свободные неизвестные 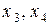 :
: 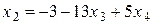 . Подставляем
. Подставляем 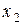 в первое уравнение и выражаем
в первое уравнение и выражаем 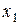 , которое становится базисной неизвестной:
, которое становится базисной неизвестной:
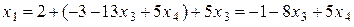 .
.
Таким образом, получаем общее решение системы:
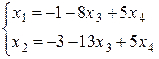 .
.
Пусть 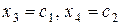 , где
, где 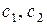 - любые действительные числа. Тогда получаем следующее решение
- любые действительные числа. Тогда получаем следующее решение
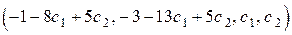 ,
,
где 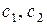 - любые действительные числа.
- любые действительные числа.
,
апрель 2011г.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 435; Нарушение авторских прав?; Мы поможем в написании вашей работы!