Теория центробежного насоса

(основное уравнение центробежного насоса).

Рассмотрим работу колеса центробежного насоса, с бесконечно большим числом, бесконечно тонких лопастей, на идеальной жидкости (жидкость невязкая, нет гидравлических потерь и завихрений потока). Проходящий через колесо поток состоит из элементарных струек, форма которых соответствует очертанию лопастей в плане.

Для вывода основного уравнения центробежного насоса используем теорему изменения момента количества движения, которую для установившегося движения можно сформулировать так. Изменение момента количества движения массы жидкости, проходящей в единицу времени при переходе от одного сечения каналу к другому сечения равно моменту внешних сил, приложенных к потоку между этими сечениями. Внешними силами являются силы, прикладываемые к потоку лопастями вращающего рабочего колеса.

Под их силовым воздействием частицы жидкости движутся от центра к периферии колеса по траекториям, соответствующим очертанию лопастей в плане. Это движение является сложным движением, состоящим из вращательного движения с окружной скоростью U и поступательной (относительной) вдоль лопасти со скоростью W.

U₁, U₂ – окружные (переносные) скорости входных и выходных кромок лопастей.

W₁, W₂ – относительные скорости на входе и выходе.

V₁, V₂ – абсолютные скорости на входе и выходе.

V_1u, V_2u – тангенциальные скорости на входе и выходе.

V_1m, V_2m – меридианные скорости на входе и выходе.

r₁, r₂ – радиус колеса на входе и выходе.

Таким образом

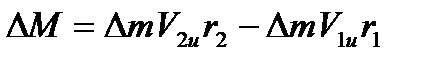,где

DМ момент внешних сил, действующий на элементарную струйку;

Dm – масса элементарной струйки, проходящей через сечение в единицу времени;

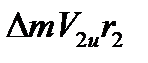– момент количества движения на выходе колеса;

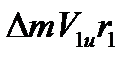– момент количества движения на входе колеса.

Для всей массы жидкости 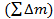, проходящей через колесо - суммарный момент внешних сил (М).

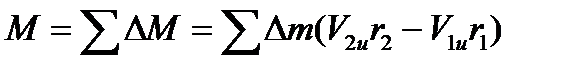
Умножим обе части уравнения на угловую скорость ω, а åDm выразим через расход жидкости, проходящий через колесо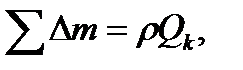

где: ρ – плотность жидкости;

Q_k – расход жидкости через колесо.

тогда

Mω = ρ Q_k (V_2ur₂ ω – V_1ur₁ ω )

Из общего курса физики известно, что:

U= rω

Mω= N

ω– угловая скорость

Mω = ρ Q_k (V_2uU₂ – V_1uU₁)

Для насоса с бесконечно большим числом лопастей, перекачивающего идеальную жидкость: Mω= N_T∞

N_T∞ = ρ Q_k (V_2uU₂ – V_1uU₁)

N_Т∞ - теоретическая мощность насоса с бесконечно большим числом лопастей.

Из курса «Гидромашины» известно, что N_Т∞=ρ H_T∞Q_k (см. курс лекций).

g – ускорение свободного падения

ρ gH_T∞Q_k = ρ Q_k (V_2uU₂ – V_1uU₁)

Отсюда:

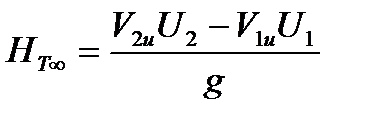
Это основное уравнение центробежного насоса или по-другому уравнение Эйлера. Чаще всего скорость V₁ направлена вдоль радиуса колеса, тогда V_1u = 0 и уравнение Эйлера принимает следующий вид:

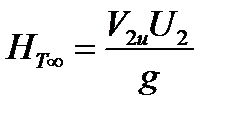
Дата добавления: 2014-11-20