
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебра логики. Операции алгебры логики
|
|
|
|
ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ
В ЭВМ информация подвергается не только арифметической, но и логической обработке. В основе работы логических схем и устройств ЭВМ лежит алгебра логики.
Алгебра логики – это раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Значения всех элементов алгебры логики определены в двухэлементном множестве 0 и 1.
Логическое высказывание – это любое повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно. Если высказывание истинно, то считают, что его значение равно единице; если высказывание ложно, то считают, что его значение равно нулю.
Пример: «Лед – твердое состояние воды» - истинное высказывание; «Все рыбы умеют плавать» - общее высказывание (истинное); «Париж – столица Китая» - ложное высказывание.
Логическая константа – ИСТИНА (1) или ЛОЖЬ (0).
Логическая переменная – символически обозначенная логическая величина, которая может принимать только значения ИСТИНА (1) или ЛОЖЬ (0).
Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Пример: Пусть А – Петров врач, В – Петров – шахматист. Тогда можно (например при помощи связки «и») составить составное высказывание: Петров – врач И шахматист (мы это поймем как «Петров – врач, умеющий играть в шахматы), А при помощи введенных обозначений мы получим: А И В.
Для К логических переменных существует 2К логических комбинаций 0 и 1.
Пример: К=2 (высказывания А и В) следовательно различных комбинаций – 4 (00, 01, 10, 11); К=3 (А, В, С) следовательно комбинаций 23=8 (000, 001, 010, 011, 100, 101, 110, 111)
Основными операциями алгебры логики являются операции конъюнкции, дизъюнкции и инверсии.
В то же время всякое устройство ЭВМ, выполняющее преобразование информации на комбинационные схемы технически реализуется с использованием логических элементов.
Логический элемент – это преобразователь, который, получая сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдает значение логического отрицания, логической суммы или логического произведения этих высказываний, т.е. обеспечивает реализацию различных логических функций от входных двоичных переменных.
Конъюнкция – логическое умножение, логическое И. Логическое умножение: операция, связывающая 2 и более высказывания с помощью союза «И». Обозначается: И, Ù, ×,&
ЗАКОН: Конъюнкция истинна тогда и только тогда, когда истинны ВСЕ входящие в нее высказывания.
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Таблица истинности для конъюнкции и графическое изображение логического элемента имеет вид:
| x | y | xÙy | Условное обозначение |
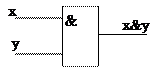
| |||
Дизъюнкция – логическое сложение, логическое ИЛИ. Логическое сложение: операция, связывающая два и более высказывания с помощью союза «ИЛИ». Обозначается: ИЛИ, V, +
ЗАКОН: Дизъюнкция истинна тогда и только тогда, когда истинно ХОТЯ БЫ ОДНО из входящих в нее высказываний.
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов.
Таблица истинности для дизъюнкции и графическое изображение логического элемента имеет вид:
| x | y | x v y | Условное обозначение |
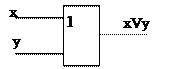
| |||
Инверсия – логическое отрицание, логическое НЕ. Логическое отрицание – это присоединение частицы «НЕ» к сказуемому высказывания. (Петров – врач. Петров – не врач). Обозначается: НЕ, 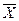 , Х.
, Х.
ЗАКОН: Если высказывание Х – истинно, то НЕ Х – ложно.
Логический элемент «НЕ» (инвертор) выдает на выходе сигнал, противоположный сигналу на входе.
Таблица истинности для инверсии и графическое изображение логического элемента имеет вид:
| x | 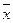
| Условное обозначение |

| ||
На основе использования основных логических схем строятся еще две логические схемы: Схема И-НЕ (элемент Шеффера) и схема ИЛИ-НЕ (элемент Пирса).
Схема И-НЕ состоит из элемента «И» и инвертора и осуществляет отрицание результата схемы «И». Связь между выходом z и входами x и y схемы записывают следующим образом: 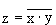 , где
, где 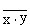 читается как «инверсия x и y».
читается как «инверсия x и y».
| x | y | 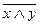
| Условное обозначение |
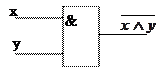
| |||
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы «ИЛИ». Связь между выходом z и входами x и y схемы записывают следующим образом: 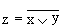 , где
, где 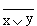 , читается как «инверсия x или y».
, читается как «инверсия x или y».
| x | y | 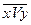
| Условное обозначение |
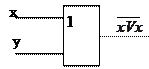
| |||
Соединяя выходы одних логических элементов со входами других логических элементов можно построить логические схемы.
Приоритет логических операций:
1) Инверсия
2) Конъюнкция
3) Дизъюнкция
Замечание: скобки могут менять приоритет операций
Пример: По заданному логическому выражению построить таблицу истинности и составить логическую схему.
а) 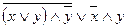
Решение: 1. Т.к. мы видим 2 логические переменные «х» и «у», то для них будет 4 различные логические комбинации 0 и 1: (0,0); (0,1); (1,0); (1,1). 2. Для построения таблицы истинности расставим сначала приоритет операций: 1) 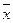 ; 2)
; 2) 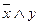 ; 3)
; 3) 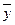 ; 4)
; 4) 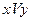 ; 5)
; 5) 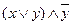 ; 6)
; 6) 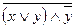 ; 7)
; 7) 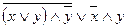
Составим таблицу истинности. В ней будет 5 строк (первая – для обозначения переменных и действий, и 4 для возможных комбинаций входных данных) и столько столбцов, сколько мы выделили отдельных операций (расставляя приоритеты) плюс количество исходных переменных:
| x | y | 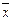
| 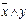
| 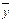
| 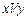
| 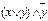
| 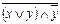
| 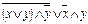
|
 Теперь изобразим логическую схему.
Теперь изобразим логическую схему.
Пример: По заданной логической схеме составить логическое выражение и заполнить для него таблицу истинности
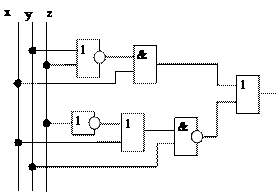 |
Решение: Во-первых, определяем, сколько входов имеется. Их в данной схеме три. Обозначаем их символами, например: x, y, z. Во-вторых, смотрим, какие логические элементы составляют схему и аккуратно изображаем эти элементы в виде формул. Получаем следующее логическое выражение: 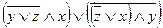 .
.
Составляем таблицу истинности. Т.к. имеется три входа, то будет 23=8 различных логических комбинаций 1 и 0.
(Заметим, что необходимо не забывать об инвертировании выражений)
| x | y | z | 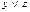
| 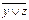
| 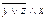
| 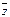
| 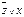
| 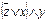
| 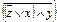
| 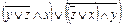
|
Задачи:
1. По заданному логическому выражению построить таблицу истинности и составить логическую схему.
а) 
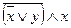
б) 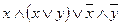
в) 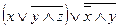
г) 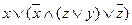
д) 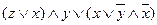
е) 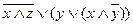
ж) 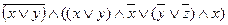
2. По заданной логической схеме составить логическое выражение и заполнить для него таблицу истинности.
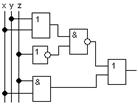 а) а)
| 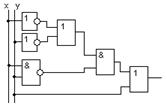 б) б)
|
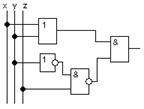 в) в)
| 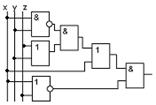 г) г)
|
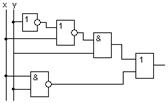 д) д)
| 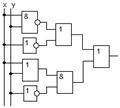 е) е)
|
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1086; Нарушение авторских прав?; Мы поможем в написании вашей работы!