Последовательный поиск

Поиск на основе сравнения ключей

Идея данного метода поиска состоит в том, чтобы в определенной последовательности считывать записи таблицы до тех пор, пока не будет считана запись, ключ которой совпадает с аргументом поиска. В простейшем случае порядок считывания и проверки записей определен заранее (последовательный поиск), в более совершенных процедурах поиска выбор следующей проверяемой записи определяется результатами сравнения с аргументом поиска ключей предыдущих считанных записей. Важным показателем сложности поиска, основанного на сравнении ключей, является число сравнений, необходимых для нахождения требуемой записи. Необходимое число сравнений в рамках заданного метода определяет время поиска. Поэтому при рассмотрении методов поиска интересуются прежде всего числом необходимых сравнений.

Этот вид поиска является единственно возможным для последовательных ЗУ, однако ввиду своей простоты и универсальности он часто применяется и для адресных ЗУ.

Алгоритм последовательного поиска заключается в следующем: на каждом шаге считывается очередная запись и ее ключ сравнивается с аргументом поиска. Шаги повторяются, начиная с первой записи таблицы, до тех пор, пока либо ключ очередной записи не совпадет с аргументом поиска, либо не будут считаны все записи таблицы. В первом случае поиск заканчивается удачно, во втором – неудачно.

В случае удачного поиска возможное число сравнений лежит в пределах [1,N], где N – число записей в таблице. Для случая неудачного поиска всегда требуется N сравнений.

Пусть значения аргумента случайны, т.е. в текущем запросе с некоторой вероятностью Q аргумент не совпадает ни с одним ключом таблицы, а с вероятностью 1-Q совпадает хотя бы с одним ключом (Q – вероятность неудачного поиска). Кроме того, в случае удачного поиска существуют вероятности p_i того, что аргумент совпадает с ключом i- й записи таблицы (). Тогда среднее число сравнений в случае удачного поиска составляет

Для равновероятных запросов ,

Среднее число сравнений с учетом как удачного, так и неудачного поиска составляет

Для равновероятных запросов аргумента последняя формула принимает вид:

Пусть записи в файле или таблице упорядочены по возрастанию ключей, т.е. K₁<K₂<…<K_N. Во многих случаях упорядочивание файла легко производится с помощью разнообразных алгоритмов сортировки. Для удачного поиска предварительное упорядочивание файла никак не влияет на необходимое среднее число сравнений, однако в случае неудачного поиска это часто позволяет завершить поиск раньше, чем будет просмотрен весь файл. Действительно, лишь только ключ очередной записи превзойдет аргумент поиска, можно будет утверждать, что требуемая запись в таблице отсутствует. Таким образом, необходимое число сравнений в этом случае лежит в пределах [1,N].

Пусть известны вероятности q_i того, что в случае неудачного поиска аргумент принимает значения A< K₁ при i=1, K_i-1<A< K_i при i=2,3,…,N и A> K_N при i=N+1. Тогда среднее число сравнений при неудачном поиске составляет…

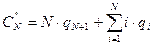
Для равновероятного случая

Среднее число сравнений при поиске в упорядоченном файле с учетом как удачного, так и неудачного поиска составляет

Для равновероятного случая эта формула принимает вид

Поскольку упорядочивание файла по ключам не влияет на сложность удачного поиска, то, если заранее известно, что поиск в большинстве случаев удачный, файл можно упорядочить по убыванию вероятностей p_i. При этом удается уменьшить среднее число сравнений: ведь чем ближе часто запрашиваемая запись к началу файла, тем меньше сравнений требуется совершить при ее поиске.

Дата добавления: 2014-11-20