B-деревья: общие сведения

Помехоустойчивый поиск

В рассмотренных методах поиска негласно предполагалось, что ключи однозначно закреплены за соответствующими записями и не содержат ошибок. Между тем очень сложно добиться того, чтобы в больших базах данных соблюдалась абсолютная точность записи значений полей всех видов. Участие человека-оператора в процедурах ввода данных делает ошибки неизбежными. Например, принято считать, что частота ошибок при вводе с клавиатуры достигает порой 1% и далеко не всегда их удается обнаружить и исправить.

Неточность данных может быть обусловлена и другими причинами. В частности, ключевое слово может быть известно только по звучанию, а некоторые собственные имена даже теоретически допускают неоднозначное написание. Следовательно, большое значение имеет построение алгоритмов, способных осуществлять поиск в условиях помех.

Например, предположим, что в роли ключей выступают слова, которые могли быть слегка искажены, и мы хотели бы найти нужную запись, несмотря на эту ошибку. Если сделать две копии файла, в одной из которых ключи расположены в обычном алфавитном порядке, а в другой они упорядочены справа налево (как если бы слова были прочитаны наоборот), искаженный аргумент поиска в большинстве случаев совпадает до половины своей длины или более с записью одного из этих двух файлов. Таким способом удается отыскать возможные претенденты на искомую запись.

Другая идея решения этой задачи состоит в том, чтобы найти некоторое преобразование аргумента в код (маску), собирающий вместе все варианты данного ключа. За рубежом нашел широкое применение следующий метод кодирования фамилий:

а) оставить первую букву; все буквы A, E, H, I, O, U, W, Y, стоящие на других местах, - вычеркнуть;

б) оставшимся буквам (кроме первой) присвоить следующие значения:

(B, F, P, V) -> 1;

(C, G, J, K, Q, S, X, Z) -> 2;

(D, T) -> 3;

L -> 4;

(M, N) -> 5;

R -> 6;

в) если в исходном имени (перед шагом а) рядом стояли несколько букв с одинаковыми кодами, пренебречь всеми, кроме первой из этой группы;

г) дописывая в случае надобности нули или опуская лишние цифры, преобразовать полученное выражение в форму «одна буква, три цифры».

Например:

Ключевое слово	Код маски
EULER	E460
GAUSS	G200
HILBERT	H416
KNUTH	K530

Разумеется, такая система собирает вместе не только родственные, но и достаточно различные имена. С другой стороны, некоторые родственные имена могут иметь различную кодировку. Но, вообще говоря, этот метод намного увеличивает вероятность обнаружить имя под одной из его масок.

На практике широко распространены модели данных в виде B-деревьев. Использование В-дерева обеспечивает высокое быстродействие поиска при удалении, добавлении и чтении записей без осуществления сортировки всего содержимого файла после каждого изменения. Отличительной особенностью деревьев данного вида является то, что в них допускается более двух ветвей, исходящих из одной вершины.

Каждая вершина В-дерева состоит из совокупности значений первичного ключа, указателей индекса и ассоциированных данных. Указатели индекса используются для перехода на следующий, более низкий уровень вершин в В-дереве. Ассоциированные данные фактически представляют собой совокупность указателей данных и служат для определения физического местоположения данных, ключевые значения которых хранятся в этой вершине индекса. Хотя записи данных можно было бы разместить непосредственно в вершинах индекса, для баз данных большой размерности такой способ оказался бы неэффективным. Обычно В-деревья используют только для организации индекса; записи данных располагаются в отдельной области.

Основные достоинства В-дерева:

1. Во всех случаях полезное использование памяти для хранения индексов составляет свыше 50%. Обеспечивается динамическое распределение и использование памяти. С ростом степени полезного использования памяти не происходит снижения качества обслуживания пользовательских запросов.

2. Произвольный доступ к записи реализуется посредством небольшого количества подопераций (обращений к физическим блокам) и по эффективности сопоставим с методами перемешивания.

3. В среднем достаточно эффективно реализуются операции включения и добавления записей. При этом сохраняется естественный порядок ключей с целью последовательной обработки, а также соответствующий баланс дерева для обеспечения быстрой произвольной выборки.

4. Упорядоченность по ключу обеспечивает возможность эффективной пакетной обработки.

Основной недостаток В-деревьев состоит в отсутствии для них средств выборки данных по вторичному ключу.

В-дерево степени k (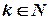) обладает следующими свойствами:

1. Все пути от корневой вершины до вершин-листьев имеют одинаковую длину h, называемую также высотой В-дерева (т.е. h есть количество вершин от корня до листа включительно).

2. Для каждой вершины, за исключением корня и листьев, количество подчиненных ей вершин (вершин-преемников) должно быть не меньше k+1 и не больше 2k+1.

3. Для корневой вершины количество подчиненных ей вершин должно быть не меньше двух и не больше 2k+1.

4. В каждой вершине, за исключением корня, количество ключей должно быть не меньше k и не больше 2k. В корне допускается только один ключ. В общем случае любая неконечная (ветвящаяся) вершина с j ключами должна иметь j+1 подчиненных вершин.

На основании этих свойств легко видеть, что B-дерево степени 1, в котором из каждой вершины выходят в точности две ветви, представляет собой полностью сбалансированное бинарное дерево поиска. Вследствие переменного количества ключей в вершинах B-деревья оказываются более гибкими в сравнении с бинарными деревьями. Так, многие операции включения и удаления можно выполнять без последующего преобразования дерева.

Физическая организация ветвящейся вершины В-дерева подобна физически последовательной структуре, как показано на рис. 2.9.

p0

k1

α1

p1

k2

α2

p2

k3

α3

…

pn-1

kn

αn

pn

Рис.2.9

Структура ветвящейся вершины B-дерева с n ключами

При реализации каждый блок (или страница), как правило, содержит только одну вершину. Поэтому в блоке 2k-n ключевых позиций и соответствующих им указателей свободны. Ключевые значения обозначены через k_i, указатели индекса - p_i, а соответствующие указатели данных - α_i.

На рис. 2.10 приведены примеры В-деревьев степеней 1, 2 и 3. В явном виде показаны действительные ключевые значения, а указатели ветвей изображены стрелками, обозначающими направление путей доступа. Ассоциированные данные, соответствующие вершинам B-дерева, на рисунке не показаны. Все листья располагаются в В-дереве на одинаковом уровне, поскольку любое B-дерево полностью сбалансировано по высоте. Отметим также, что независимо от степени дерева его корень может иметь самое меньшее один ключ.

Рис.2.10

Возможные конфигурации В-дерева для файла с 12 ключами:

а) дерево степени 1 (h=3);

б) дерево степени 2 (h=2);

в) дерево степени 3 (h=2).

По мере возрастания степени В-дерева его высота уменьшается. Следовательно, при условии размещения каждой вершины в отдельном блоке или на отдельной странице В-дерево обеспечивает ускорение поиска по сравнению с бинарным деревом.

Алгоритм поиска для В-дерева аналогичен алгоритму поиска в бинарном дереве. Выполняется просмотр упорядоченных ключей в вершине с целью поиска хранимого ключа (индекса), равного или большего аргумента поиска. Если найден ключ, равный аргументу поиска, поиск считается завершившимся удачно и для определения местоположения записи используется значение указателя данных. Если в некоторой позиции найден ключ k_i, больший аргумента поиска, то осуществляется переход на вершину следующего уровня в соответствии со значением предыдущего указателя индекса p_i-1 и просмотр ключей в данной вершине. Если же все хранимые в вершине ключи меньше аргумента поиска, то осуществляется переход на следующий уровень в соответствии со значением самого правого указателя индекса p_n. Если аргумент поиска не найден в вершине-листе, то поиск заканчивается неудачно. Так, на рис. 2.10 поиск ключа 25 потребует: в случае а – трех обращений к блокам, в случае б – одного обращения к блоку и в случае в – двух обращений к блокам.

Дата добавления: 2014-11-20