Порядок выполнения работы. Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником

Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником

Задание

Используйте придуманную вами задачу разработки управленческого решения. Задайтесь параметром, который может быть в условиях неопределенности в результате возможных действий противника. Рассматривайте случай дуальной игры с противником с нулевой суммой и решите задачу.

1. Из общего числа параметров вашей задачи разработки управленческого решения выберите один, который будет рассматриваться в условиях неопределенности. Согласуйте с преподавателем выбранный вами параметр.

2. На основе анализа ситуации в зависимости от возможных действий противника задайтесь 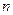возможными значениями случайного параметра 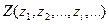, для которых будет делаться расчет. Каждое значение этого параметра будет определять одну из наших стратегий и одну из возможных стратегий противника.

3. Решая задачу с помощью надстройки Поиск решения, определите значение критериальной функции и соответствующие ему решения в предположении, что стратегия противника угадана, то есть мы предполагаем значение параметра 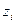, и в результате действий противника он принимает именно такое значение.

4. Постройте платежную матрицу, заполните ее диагональ значениями 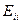и отдельно запишите соответствующие им решения .

5. Используя выражение для показателя эффективности, рассчитайте значения критериальной функции 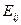в предположении, мы используем стратегию 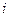, то есть решение , а в результате действий противника параметр принимает значение .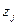

6. Заполните значениями 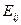свободные клетки платежной матрицы.

7. Просматривая колонки платежной матрицы (), найдите для каждой строки 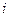наш гарантированный минимальный выигрыш .

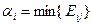8. Найдите номер нашей стратегии, обеспечивающей нам максимум гарантированного выигрыша (нижнюю цену игры) .

9. Просматривая строки платежной матрицы (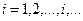), найдите для каждого столбца гарантированный максимальный проигрыш противника (верхнюю цену игры) .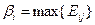

10. Найдите номер стратегии противника, обеспечивающей ему минимум гарантированного выигрыша .

11. Сравните верхнюю и нижнюю цены игры и определите факт наличия или отсутствия седловой точки.

12. Если седловая точка существует (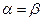), то определите оптимальное решение задачи соответствующее номеру чистой стратегии, обеспечивающей .

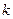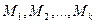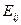13. Если седловая точка отсутствует (), то определите набор своих стратегий , которые обеспечивают значение , имеют свой выигрыш и будут чередоваться нами в случайном порядке. Аналогично определите набор стратегий противника . Сформируйте новую матрицу 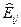размером 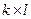, элементы которой представляют выборку из платежной матрицы в соответствии с принятыми в рассмотрение стратегиями.

14. Отдельно сформулируйте и решите еще одну задачу линейного программирования, принимая во внимание ограничений

15. В соответствии с полученным решением по формуле 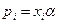определите набор вероятностей , с которыми необходимо чередовать стратегии .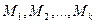

Контрольные вопросы

1. Чем задача в условиях неопределенности отличается от задачи в условиях риска?

2. Что такое стратегия?

3. Что такое дуальная игра?

4. В каком случае игра может называться игрой с нулевой суммой?

5. В каком случае игра классифицируется как игра с противником?

6. Как составляется платежная матрица?

7. Чем элементы диагонали платежной матрицы отличаются от других элементов?

8. Что такое седловая точка?

9. В каком случае седловая точка может отсутствовать?

10. Что такое нижняя и верхняя цены игры?

Дата добавления: 2014-11-20