Игры с природой

Отчет о работе

Подготовьте отчет о выполненной лабораторной работе. Он должен содержать титульный лист, формулировку задания, исходные данные, описание проблемы, которая была разрешена. Укажите случайный параметр, взятый в рассмотрение, и обоснуйте его выбор. Приведите обоснование выбора его значений. Представьте платежную матрицу и результаты ее обработки. Определите факт наличие или отсутствия седловой точки. Если она существует, то приведите результаты решения задачи. Если седловой точки нет, то приведите набор стратегий, взятых в рассмотрение, представьте формулировку и результаты решения задачи определения набора вероятностей, с которыми будут чередоваться стратегии, и поставьте каждой в соответствие решение. Сформулируйте выводы, которые можно сделать по результатам выполненной работы.

Пример содержания отчета о выполнении лабораторной работы приведен в приложении Б.

Отличительной особенностью игр с природой является то обстоятельство, что природа рассматривается как некоторая незаинтересованная инстанция, поведение которой неизвестно, но, во всяком случае, не содержит элемента враждебности и сознательного противодействия достижению наших целей. Как и в случае игр с противником, нам должна быть известна платежная матрица, соответствующая нашему выигрышу при различных своих стратегиях и состояниях (стратегиях) природы. Если в случае игры с противником предполагать определенные вероятности появления его стратегий не представлялось возможным, то в рассматриваемой ситуации нам полезно дополнительно располагать информацией о вероятностях появления возможных состояний природы, заданной, например, в виде смешанных стратегий

,

.

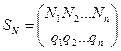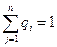Задача заключается в выборе в конкретных условиях наиболее выгодной собственной стратегии, а отбрасывать «невыгодные» с точки зрения природы стратегии нельзя. Исходя из этого в теории статистических решений [3] вводится понятие риска

,

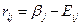где 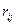наш риск при использовании стратегии 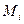в ответ на состояние природы , а 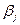- максимально возможный наш выигрыш при состоянии природы . Если нам известны вероятности возможных состояний природы , то было бы логичным в качестве своей стратегии принять одну из наших возможных стратегий , максимизирующую наш средний выигрыш

.

Отметим, что указанная стратегия одновременно минимизирует средний риск.

Примечание. В случае игры с природой количество наших возможных стратегий 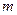может отличаться от количества возможных стратегий природы .

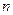При выборе оптимальной стратегии одну из существенных трудностей представляет определение конкретного набора вероятностей . Если нет никаких гипотез о вероятности появления определенного состояния природы, то используется принцип недостаточного основания Лапласа, когда вероятности назначаются равными друг другу

.

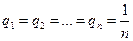Если у нас существуют некоторые предположения о вероятностях появления определенных событий, то мы можем их расставить в порядке убывания их правдоподобности (ранжировать) и поставить им в соответствие некоторый ряд чисел, определенный, в том числе, и экспертным путем. Отметим, что в любом случае справедливо утверждение

.

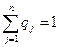Дата добавления: 2014-11-20