КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предметный указатель 4 страница
|
|
|
|
Таблица П29. Оптимальный выпуск продукции по критерию 3
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход |
| Количество (шт.) | 0,00 | 0,00 | 0,00 | 15,12 | 0,00 | 29,54545 | |||
| Цена (руб.) | 863,0435 |
Таблица П30. Расход ресурсов на выпуск продукции по критерию 3
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | 133,9921 | <= | |||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 22,26 | <= | ||||
| Ресурс 3 (ед. измерения) | 650,00 | <= | |||||||||
| Ресурс 4 (ед. измерения) | 104,4466 | <= | |||||||||
| Ресурс 5 (ед. измерения) | 120,95 | <= | |||||||||
| Ресурс 6 (ед. измерения) | <= | ||||||||||
| Ресурс 7 (ед. измерения) | 253,56 | <= | |||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 32,78 | <= | ||
| Ресурс 9 (ед. измерения) | 371,74 | <= | |||||||||
| Ресурс 10 (ед. измерения) | 521,54 | <= | |||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 11,39 | <= | |
| Ресурс 12 (ед. измерения) | 1826,383 | <= | |||||||||
| Ресурс 13 (ед. измерения) | 654,15 | <= | |||||||||
| Ресурс 14 (ед. измерения) | 164,23 | <= | |||||||||
| Ресурс 15 (ед. измерения) | 922,1344 | <= |
Очевидно, что оптимальное решение по одному критерию не совпадает с оптимальным решением по другим, т.е. критерии противоречивы. Задались вектором важности критериев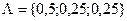 
и решили задачу методом скаляризации векторного критерия воспользовавшись формулой:
.
Оптимальное решение при выбранной схеме компромисса и заданных значениях вектора важности имеет вид {21,18; 0; 0; 19,61; 3,19; 0; 0; 0}, а
.
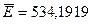Значения локальных критериев равны соответственно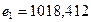 
, 
, 
.
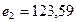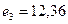При другом векторе важности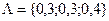 
:
.
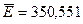При этом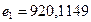 
; 
; 
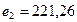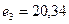, а оптимальное решение имеет вид {0; 0; 0; 26,44; 0; 17,82; 0; 0}.
Воспользовались методом квазиравенства, при реализации которого добиваются обеспечения разности между величинами локальных критериев, не превышающих некоторой заданной величины 
. Предположили, что все локальные критерии имеют одинаковые единицы измерения. Тогда
, 
.
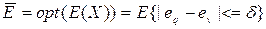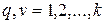Пусть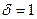 
. Установили в качестве целевой ячейку, содержащую расчет дохода, а выражения 
, 
, 
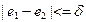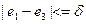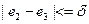записали как дополнительные ограничения. Решая задачу оптимизации, получили таблицы П31 и П32:
Таблица П31. Оптимальный выпуск продукции по принципу квазиравенства
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход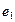 
| Критерий 2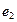 
| Критерий 3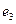 
|
| Количество (шт.) | 0,088889 | 0,011111 | |||||||||
| Цена (руб.) | 1,088888846 | 0,088889 | 0,088889 |
Таблица П32. Расход ресурсов на выпуск продукции по принципу квазиравенства
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | 0,3 | <= | |||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 0,003333332 | <= | ||||
| Ресурс 3 (ед. измерения) | 2,666666826 | <= | |||||||||
| Ресурс 4 (ед. измерения) | 0,833333365 | <= | |||||||||
| Ресурс 5 (ед. измерения) | 0,088888846 | <= | |||||||||
| Ресурс 6 (ед. измерения) | 2,211111106 | <= | |||||||||
| Ресурс 7 (ед. измерения) | 0,788888894 | <= | |||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 0,088888889 | <= | ||
| Ресурс 9 (ед. измерения) | 0,7 | <= | |||||||||
| Ресурс 10 (ед. измерения) | 1,122222212 | <= | |||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 0,040555558 | <= | |
| Ресурс 12 (ед. измерения) | 4,566666778 | <= | |||||||||
| Ресурс 13 (ед. измерения) | 1,822222259 | <= | |||||||||
| Ресурс 14 (ед. измерения) | 0,233333317 | <= | |||||||||
| Ресурс 15 (ед. измерения) | 1,977777788 | <= | |||||||||
|
| |||||||||||
|
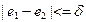
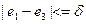
| 0,999999957 | 0,999999957 | |||||||||
|
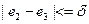
| 4,29969E-08 | 4,29969E-08 |
Решение задачи оптимизации по принципу максимина совпадает с решением при максимизации локального критерия 3 (таблица П29), поскольку он во всех трех случаях имеет минимальное значение.
Принцип абсолютной уступки соответствует критерию:
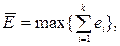
В нашем случае составляет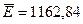 
, при этом 
, 
, 
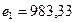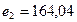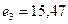. Вектор решения равен {11,58; 0; 0; 23,51; 0; 9,30; 0; 0}.
Компромисс по принципу последовательной уступки. Предположили, что критерии ранжированы по важности в соответствии с их номерами. Нашли оптимальное решение по критерию 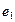. Назначили уступку 
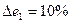, которая вносится в качестве ограничения и позволяет максимизировать значение локального критерия 
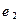. Тогд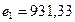а 
, а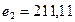 
. Ввели уступку по второму критерию 
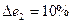и максимизировали значение показателя 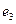. Тогд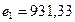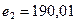а ; 
, а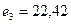 
. Вектор решения имеет вид {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07}.
3. Выводы:
Результаты решения многокритериальной задачи, полученные с помощью различных методов выбора компромисса, сведены в таблицу П33.
Таблица П33. Результаты решения многокритериальной задачи на основе различных принципов выбора компромисса
| Метод |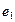
|
|
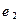
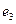
| Решение |
| Скаляризации векторного критерия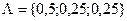
| 1018,41 | 123,59 | 12,36 | {21,18; 0; 0; 19,61; 3,19; 0; 0; 0} |
| Скаляризации векторного критерия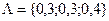
| 920,11 | 221,26 | 20,34 | {0; 0; 0; 26,44; 0; 17,82; 0; 0} |
| Максимин | 863,04 | 120,95 | 32,78 | {0,00; 0,00; 0; 0,00; 15,12; 0; 0,00; 29,55} |
| Квазиравенство | 1,09 | 0,09 | 0,09 | {0; 0; 0,088889; 0; 0,011111; 0; 0; 0} |
| Принцип абсолютной уступки | 983,33 | 164,04 | 15,47 | {11,58; 0; 0; 23,51; 0; 9,30; 0; 0} |
| Принцип последовательной уступки | 931,33 | 190,01 | 22,42 | {0; 0; 0; 22,69; 0,01; 15,29; 0; 7,07} |
Пример содержания отчета по лабораторной работе №10 «Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической»
1. Исходные данные:
Предприятие выпускает восемь видов товаров. Для производства указанных товаров используется 15 видов ресурсов. Рассматривалась проблема недостаточности дохода предприятия. Требуется определить программу производства товаров различного вида, обеспечивающую максимум среднего дохода предприятия. Параметры задачи представлены теми же числовыми данными, которые использовались при выполнении работы №2. Предполагается, что цена товара 1 изменяется в течение времени и на первом дискретном моменте планирования имеет значение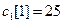 
, а на втором ‑ 
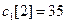. Кроме этого, рассматривается два варианта использования ресурсов. В первом случае предполагается, что для каждого отсчета времени ресурсы возобновляются в прежнем объеме. Во втором случае предполагается, что уже в первом интервале времени ресурсы двух интервалов доступны в полном объеме, а ресурсы, не использованные в первом отсчете времени, сохраняются и могут быть использованы во втором.
2. Решение.
Оптимальное решение статической задачи при 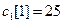представлено в таблицах П34 и П35, а при 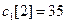в таблицах П36 и П37.
Таблица П34. Решение при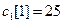
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход |
| Количество (шт.) | 13,93127 | 3,200906 | 5,386733 | 0,599527 | 20,1504 | ||||
| Цена (руб.) | 1034,812 |
Таблица П35. Ресурсы при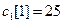
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | <= | ||||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 13,69 | <= | ||||
| Ресурс 3 (ед. измерения) | 546,25 | <= | |||||||||
| Ресурс 4 (ед. измерения) | <= | ||||||||||
| Ресурс 5 (ед. измерения) | 31,73 | <= | |||||||||
| Ресурс 6 (ед. измерения) | <= | ||||||||||
| Ресурс 7 (ед. измерения) | 351,68 | <= | |||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 9,12 | <= | ||
| Ресурс 9 (ед. измерения) | 368,90 | <= | |||||||||
| Ресурс 10 (ед. измерения) | 620,80 | <= | |||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 9,90 | <= | |
| Ресурс 12 (ед. измерения) | <= | ||||||||||
| Ресурс 13 (ед. измерения) | 669,27 | <= | |||||||||
| Ресурс 14 (ед. измерения) | 69,20 | <= | |||||||||
| Ресурс 15 (ед. измерения) | <= |
Таблица П36. Решение при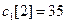
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход |
| Количество (шт.) | 35,60091 | 2,721088 | 2,947846 | ||||||
| Цена (руб.) | 1373,469 |
Таблица П37. Ресурсы при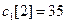
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | 96,8254 | <= | |||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 22,06349 | <= | ||||
| Ресурс 3 (ед. измерения) | 492,517 | <= | |||||||||
| Ресурс 4 (ед. измерения) | <= | ||||||||||
| Ресурс 5 (ед. измерения) | 14,73923 | <= | |||||||||
| Ресурс 6 (ед. измерения) | 814,059 | <= | |||||||||
| Ресурс 7 (ед. измерения) | 348,5261 | <= | |||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 3,106576 | <= | ||
| Ресурс 9 (ед. измерения) | 332,8798 | <= | |||||||||
| Ресурс 10 (ед. измерения) | 509,2971 | <= | |||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 9,138322 | <= | |
| Ресурс 12 (ед. измерения) | <= | ||||||||||
| Ресурс 13 (ед. измерения) | 556,0091 | <= | |||||||||
| Ресурс 14 (ед. измерения) | 85,03401 | <= | |||||||||
| Ресурс 15 (ед. измерения) | <= |
Для решения динамической задачи в Excel построена совместная таблица П36 с данными динамической задачи. Она образована как результат слияния данных задачи пр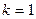и 
и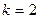 
. Исходя из особенностей входного диалога надстройки Поиск решения, все изменяемые переменные размещены в смежных ячейках, а рассчитываемые колонки Расход ресурсов сгруппированы в правой части. Решение осуществлялось средствами надстройки Поиск решения. В качестве целевой использовалась дополнительная ячейка, содержащая сумму доходов пр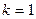и и 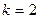. Изменяемыми параметрами были ячейки Количество (шт.) обоих интервалов планирования, а в качестве ограничений использовались ограничения первого и второго отсчетов 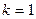и 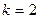. Исходные данные и некоторые результаты решения задачи в предположении, что для каждого отсчета времени имеется один и тот же набор ресурсов представлены в таблице П38.
Далее было предположено, что с самого начала в нашем распоряжении имелись ресурсы сразу двух интервалов планирования. Не использованные в первом интервале ресурсы полностью переходили на второй интервал. Остаток ресурсов для 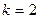вычислялся в соответствующей ячейке по формуле как разность между общим количеством ресурсов и их количеством, израсходованном в первом интервале времени таблица П39.
3. Выводы:
Результаты решения задачи приведены в таблицах П40 и П41.
Таблица П38. Данные динамической задачи пр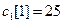и и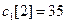
| Номер отсчета |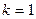
|
|
|
| ||||||||||||||||||
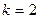
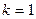
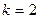
| Товары | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Доход | Доход | ||||
| Количество (шт.) | 13,93 | 3,20 | 5,39 | 0,60 | 20,15 | 35,60 | 2,72 | 2,95 | ||||||||||||||
| Цена (руб.) | 1034,81178 | 1373,46939 | ||||||||||||||||||||
| Ресурсы | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Товар 1 | Товар 2 | Товар 3 | Товар 4 | Товар 5 | Товар 6 | Товар 7 | Товар 8 | Расход ресурса | Знак нера-венства | Наличие | Расход ресурса | Знак нера-венства | Наличие |
| Ресурс 1 (ед. измерения) | <= | 96,83 | <= | |||||||||||||||||||
| Ресурс 2 (ед. измерения) | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 0,5 | 0,7 | 0,8 | 0,3 | 0,6 | 13,70 | <= | 22,06 | <= | ||||||||
| Ресурс 3 (ед. измерения) | 546,25 | <= | 492,51 | <= | ||||||||||||||||||
| Ресурс 4 (ед. измерения) | <= | <= | ||||||||||||||||||||
| Ресурс 5 (ед. измерения) | 31,73 | <= | 14,74 | <= | ||||||||||||||||||
| Ресурс 6 (ед. измерения) | <= | 814,06 | <= | |||||||||||||||||||
| Ресурс 7 (ед. измерения) | 351,68 | <= | 348,53 | <= | ||||||||||||||||||
| Ресурс 8 (ед. измерения)) | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 0,6 | 0,9 | 0,5 | 0,8 | 0,4 | 0,2 | 0,7 | 9,12 | <= | 3,11 | <= | ||||
| Ресурс 9 (ед. измерения) | 368,90 | <= | 332,88 | <= | ||||||||||||||||||
| Ресурс 10 (ед. измерения) | 620,80 | <= | 509,30 | <= | ||||||||||||||||||
| Ресурс 11 (ед. измерения) | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 0,22 | 0,35 | 0,45 | 0,12 | 0,05 | 0,19 | 0,25 | 0,36 | 9,90 | <= | 9,14 | <= | ||
| Ресурс 12 (ед. измерения) | <= | <= | ||||||||||||||||||||
| Ресурс 13 (ед. измерения) | 669,27 | <= | 556,01 | <= | ||||||||||||||||||
| Ресурс 14 (ед. измерения) | 69,20 | <= | 85,03 | <= | ||||||||||||||||||
| Ресурс 15 (ед. измерения) | <= | <= |
Таблица П39. Решение динамической задачи пр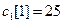и и 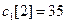с учетом перераспределения ресурсов
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 398; Нарушение авторских прав?; Мы поможем в написании вашей работы!