Пример выполнения работы № 5

ЛАБОРАТОРНАЯ РАБОТА № 5

«Вычисление кратных интегралов»

Цель работы: Научить студентов использовать возможности прикладных математических пакетов MAPLE при вычислении кратных интегралов.

Задания

1. Вычислить повторные интегралы.

2. Вычислить кратные интегралы.

Варианты заданий

Вариант 1

1. а) 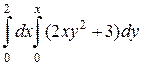; б) .

2. а)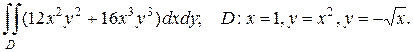

б) 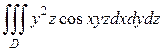, где область 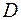ограничена поверхностями

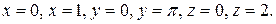
Вариант 2

1. а) 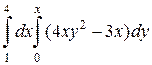; б) .

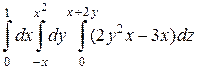2. а)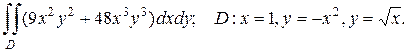

б) ,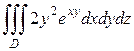

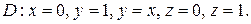
Вариант 3

1. а) ; б) .

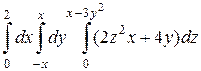2. а)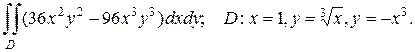

б)

Вариант 4

1. а) 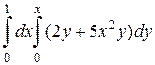; б) .

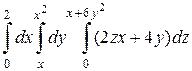2. а)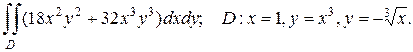

б)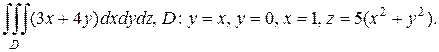

Вариант 5

1. а) 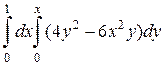; б) .

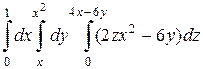2. а)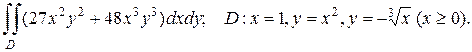

б)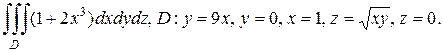

Вариант 6

1. а) 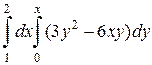; б) .

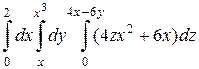2. а)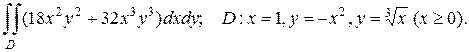

б)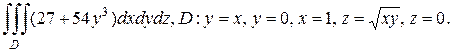

Вариант 7

1. а) 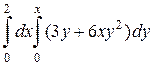; б) .

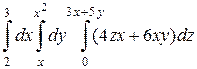2. а)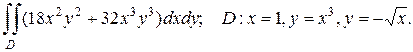

б)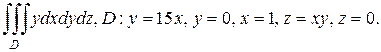

Вариант 8

1. а) 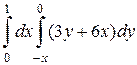; б) .

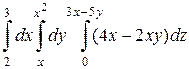2. а)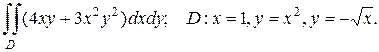

б)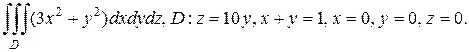

Вариант 9

1. а) 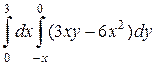; б) .

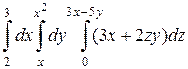2. а)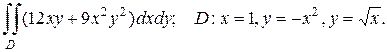

б)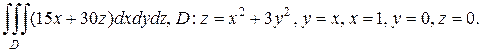

Вариант 10

1. а) 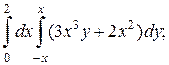б) .

2. а)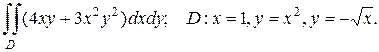

б)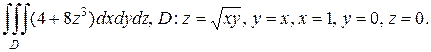

Вариант 11

1. а) 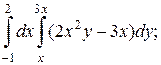б) .

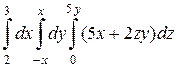2.а)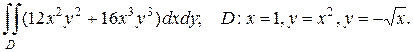

б)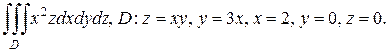

Вариант 12

1. а) 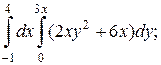б) .

2.а)

б)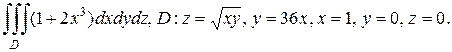

Вариант 13

1. а) 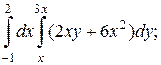б) .

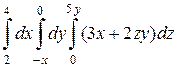2.а)

б)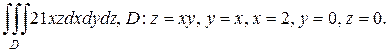

Вариант 14

1. а) 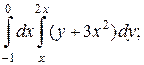б) .

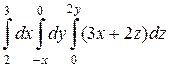2.а)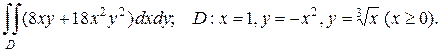

б)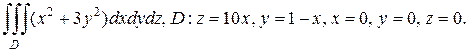

Вариант 15

1. а) 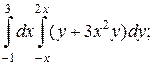б) .

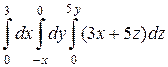2.а)

б)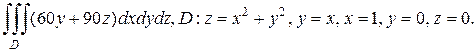

Вариант 16

1. а) б) .

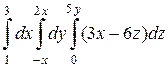2.а)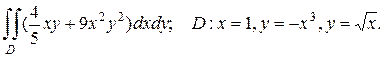

б)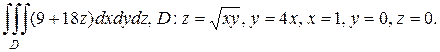

Вариант 17

1. а) б) .

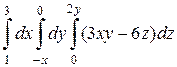2.а)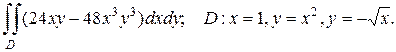

б)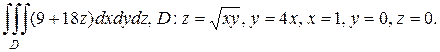

Вариант 18

1. а) 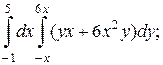б) .

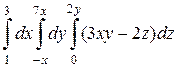2.а)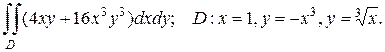

б)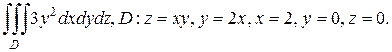

Вариант 19

1. а) 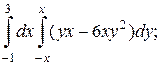б) .

2. а)

б)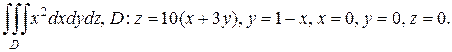

Вариант 20

1. а) б) .

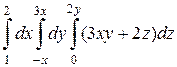2. а)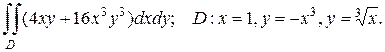

б)

Вариант 21

1. а) 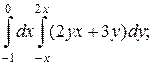б) .

2.а)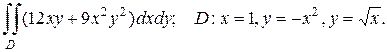

б)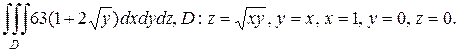

Вариант 22

1. а) 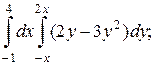б) .

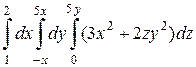2. а)

б)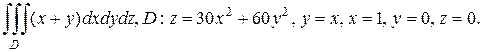

Вариант 23

1. а) 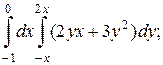б) .

2.а)

б)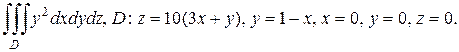

Вариант 24

1. а) 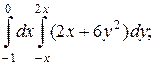б) .

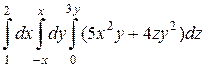2.а)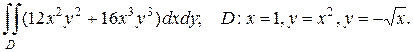

б)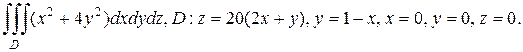

Вариант 25

1. а) б) .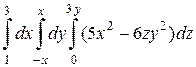

2. а)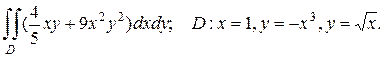

б)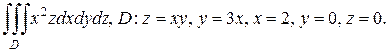

1. Вычислить повторные интегралы:

а) 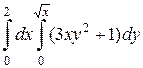; б) .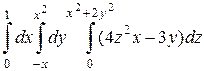

2. Вычислить кратные интегралы:

а) 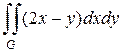, где область 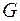ограничена линиями ;

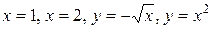б) 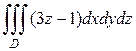, где область 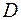ограничена поверхностями

.

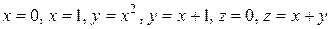1. а) Введем повторный интеграл из условия задачи и вычислим его

>I nt(Int(3*x*y^2+1,y=0..sqrt(x)),x=0..2)= int(int(3*x*y^2+1,y=0..sqrt(x)), x=0..2);

б) Введем повторный интеграл и вычислим его

>Int(Int(Int(4*z^2*x-3*y,z=0..x^2+2*y^2),y=-x..x^2),x=0..1)= int(int(int(4*z^2*x-3*y,z=0..x^2+2*y^2),y=-x..x^2),x=0..1);

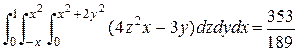
2. а) Область интегрирования представляет собой множество 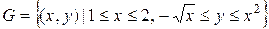. Построим область .

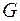> m:=plot([-sqrt(x),x^2],x=1..2,color=[red,red]):

>with(plots):

> k:=implicitplot(x=1,x=1..2,y=-1..1,color=red):

>k1:=implicitplot(x=2,x=1..2,y=-sqrt(2)..4,color=red):

> display([m,k,k1]);

Вычислим двойной интеграл как повторный .

>Int(Int(2*x-y,y=-sqrt(x)..x^2),x=1..2)= int(int(2*x-y,y=-sqrt(x)..x^2),x=1..2);

=

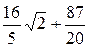
б) Область интегрирования можно задать системой неравенств:

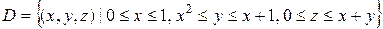. Построим проекцию области 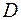на плоскость .

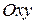> m:=plot([x+1,x^2],x=0..1,color=[red,red]):

> k:=implicitplot(x=0,x=0..1,y=0..1,color=red):

>k1:=implicitplot(x=1,x=0..1,y=1..2,color=red):

> display([m,k,k1]);

Тогда тройной интеграл сводится к повторному .

> Int(Int(Int(3*z-1,z=0..x+y),y=x^2..x+1),x=0..1)= int(int(int(3*z-1,z=0..x+y),y=x^2..x+1),x=0..1);

=

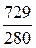
Контрольные вопросы

1. Сформулируйте определение двойного интеграла.

2. В чем состоит геометрический смысл двойного интеграла?

3. Какими свойствами обладает двойной интеграл?

4. Сформулируйте теорему о сведении двойного интеграла к повторному.

5. Что представляет собой определитель Якоби? Как производится замена переменных в двойном интеграле?

6. Как производится вычисление двойного интеграла в полярных координатах?

7. Сформулируйте определение тройного интеграла.

8. В чем состоит геометрический смысл тройного интеграла?

9. Сформулируйте теорему о сведении тройного интеграла к повторному.

10. Как производится вычисление тройного интеграла в цилиндрических и сферических координатах?

ПРИЛОЖЕНИЕ

Дата добавления: 2014-11-08