Примеры решения задач. Тема 9. Статистические методы обработки экспериментальных данных

Тема 9. Статистические методы обработки экспериментальных данных.

Тема 8. Статистическое оценивание и проверка гипотез.

Тема 7. Теория вероятностей

УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 2

Калемаев, гл. I, задачи 1.1-1.5; гл.II, задачи 2.1-2.5; гл. III, задачи 3.1-3.16; гл. IV, задачи 4.1-4.10. Разбери решение задач 1-9 из данного пособия.

Калемаев, гл.VII, задачи 7.1-7.6; гл. VIII, задачи 8.1-8.10; гл. IX, задачи 9.1-9.6; гл.XX, задачи 10.1-10.10. Разбери решение задач 10-13 из данного пособия.

Калемаев: гл.XI, задачи 11.1, 11.2; гл. XII, задачи 12.1, 12.2. Разбери решение задач 14, 15 из данного пособия.

1. Теория вероятностей – это раздел математики, изучающий количественные закономерности случайных явлений, т.е. таких, которые при неоднократном воспроизведении в одинаковых условиях могут протекать по разному. Объектами, которыми оперирует теория вероятностей, являются:

- Случайное событие – всякий факт, который может произойти или не произойти в результате случайного явления;

- случайная величина – некоторое числовое значение появляющееся в результате случайного явления.

Задача 1. Дано вероятность попадания по мишени – 0,3. Требуется определить вероятность попадания с третьего раза.

Решение: Последнее событие наступает при одновременном наступлении: 1) первый раз промахнулся; 2) второй раз промахнулся; 3) третий раз попал.

p(Ā Ā A) = p(Ā)´p(Ā)´p(A)=0,7´0,7´0,3 = 0,147

Задача 2. Дано среди 10 шаров 2 – черные. Требуется определить вероятность с двух попыток вытащить оба этих шара?

Решение. Обозначив A – первый раз вытащить черный, B - второй раз вытащить черный: p (оба раза - черные) = p (AB) = p (A) ´ p (B | A) = 2/10 ´ 1/9 = 1/45

Задача 3. Дано среди 10 шаров 1 – черный. Десять человек по очереди вытаскивают шар. Требуется определить у кого из них наибольшая вероятность вытащить черный?

Решение. Обозначив A ₁ – первый вытащил черный шар,... p (A ₁) = 1/10; p (второму достался черный) = p (Ā ₁ A ₂) = p (Ā ₁) ´ p (A ₂ / Ā ₁) = 9/10 ´ 1/9 = 1/10; p (третьему достался черный) = p (Ā ₁ Ā ₂ A ₃) = p (Ā ₁) ´ p (Ā ₂ / Ā ₁) ´ p (A ₃ / Ā ₂ Ā ₁) = 9/10 ´ 8/9´ 1/8 = 1/10 и т.д.,

т.е. все участники розыгрыша имеют одинаковые шансы вытащить черный шар независимо от порядка вытаскивания.

Задача 4. Дано участники группы захвата и группы поддержки атакуют преступников и производят по месту их укрытия две независимые очереди из автоматического оружия. Вероятность поразить цель первой очередью равна 0,2, второй - 0,3. Если преступники не поражены, то они оказывают вооруженное сопротивление и поражают участников операции с вероятностью 0,25. Требуется определить вероятность потерь среди участников операции при условии, что преступники не поражены.

Решение: 1. При использовании теоремы сложения и умножения вероятностей можно определить вероятность поражения от применения оружия с обеих сторон - сотрудников органов внутренних дел и преступников.

2. Вероятность не поражения преступников первой очередью:

Р1 = 1 - 0,2 = 0,8;

3. Вероятность не поражения преступников второй очередью:

Р2 = 1 - 0,3 = 0,7;

4. Вероятность не поражения преступников:

Р = Р1*Р2 = 0,8*0,7 = 0,56;

5. Вероятность поражения преступников

1 - Р = 1 - 0,56 = 0,44.

6. Вероятность потерь среди участников операции:

Р*0,25 = 0,56*0,25 = 0,14.

Задача 5. Дано в тире соревнуются в стрельбе из пистолета два курсанта - Иванов и Петров. Числа очков, выбиваемых каждым курсантом при одном выстреле, являются случайными величинами Х1 и Х2. Они характеризуются следующими законами распределения:

..............................................................................................................................

Случайная величина Х1 Случайная величина Х2

(Иванов) (Петров)

..............................................................................................................................

Число очков 6 7 8 9 10 6 7 8 9 10

..............................................................................................................................

Вероятность 0,2 0,1 0,25 0,3 0,15 0,1 0,15 0,3 0,25 0,2

..............................................................................................................................

Требуетсяопределитьто стреляет лучше?

Решение. 1. Вычислим математического ожидания числа выбиваемых курсантами очков:

М(х1) = 6х0,2 + 7х0,1 + 8х0,25 + 9х0,3 + 10х0,15 = 8,1

М(х2) = 6х0,1 + 7х0,15 + 8х0,3 + 9х0,25 + 10х0,2 = 8,3.

То обстоятельство, что М(х2) > М(х1) означает, что при большем числе выстрелов

курсант Петров выбьет большее число очков.

2. Вычисление дисперсии по формуле .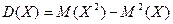

.

;

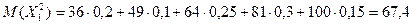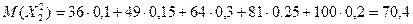
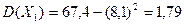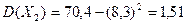
Дисперсия – это рассеяние возможных значений случайной величины вокруг ее среднего значения. Так как 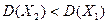, следовательно, кучность попадания Петрова выше.

Вывод: курсант Петров стреляет лучше.

Задача 6. Дано всхожесть семян данного растения составляет 90 %. Требуется найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.

Решение. 1. Если производится п независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события 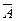равна q=1-p, то вероятность Р_п(т) того, что при этом событие А осуществляется ровно т раз, вычисляется по формуле Бернулли

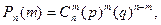(1)

где 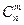есть число сочетаний из п элементов по т.

2. По условию задачи вероятность всхожести семян р =0,9; тогда q =0,1; в данном случае п =5 и т =4. Подставляя эти данные в формулу Бернулли (1), получают

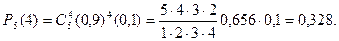
3. Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом, Р(А)=Р₅(4)+Р₅(5). Первое слагаемое уже найдено. Для вычисления второго снова применяют формулу (1):

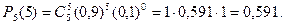
Следовательно, Р(А)=0,328+0,591=0,919.

Задача 7. Дано вероятность появления события А в каждом из 625 испытаний равна 0,64. Требуется найти вероятность того, что событие А в этих испытаниях появиться ровно 415 раз.

Решение. 1. Если число испытаний п велико, то применение формулы Бернулли приводит к громоздким вычислениям. В таких случаях применяют приближенную формулу, которая выражает суть локальной теоремы Лапласа.

Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р, а число п достаточно велико, то вероятность Р_п(т) того, что в этих испытаниях событие А наступит т раз (безразлично, в какой последовательности) вычисляется приближенно по формуле

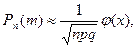(2)

где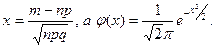

Имеются готовые таблицы значений функции j(х) (табл. П.1).

2. Для х >5 считают, что j(х)»0. Так как функция j(х) четная, то j(-х)=j(х). По условию задачи п =625, т =415, р =0,64. Находят q =1-0,64=036. Определяют значение х при этих данных:

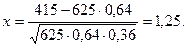
3. По табл. П1 находят, что j(1,25) =0,1826. Подставив это значение в (2), получают

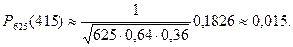
Задача 8. Дано среди семян ржи 0,04 % сорняков. Требуется определить вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

Решение. 1. Применение асимптотической формулы (2) для случая, когда вероятность р близка к нулю, приводит к значительному отклонению от точного значения Р_п(т). При малых значениях р (и при малых значениях q) применяют асимптотическую формулу Пуассона.

Если вероятность появления события А в каждом из п независимых испытаний мала, а число испытаний п достаточно велико, то вероятность того, что событие А наступит т раз, вычисляется приближенно по формуле

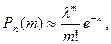(3)

где l =пр.

Формулу (3) применяют в тех случаях, когда l £10. При этом чем больше число п и меньше число р, тем точнее результат по этой формуле.

2. По условию задачи п =5000, т =5, р =0,0004. Тогда l =5000^.0,0004=2. Применяя (3), получают

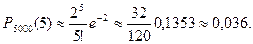
Задача 9. Дано: имеются три одинаковых на вид урны. В них находятся:

в первой урне – 2 белых и 1 черный шар;

во второй урне – 3 белых и 1 черный шар;

в третьей урне – 2 белых и 2 черных шара.

Требуется:

- некто выбирает наугад одну из урн и вынимает из нее шар, найти вероятность того, что это шар белый.

- из случайно выбранной урны вытащен белый шар, найти вероятность того, что он вытащен из второй урны.

Решение. 1. Рассматривают три гипотезы:

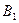- выбор первой урны,

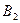- выбор второй урны,

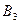- выбор третьей урны,

и событие А - появление белого шара.

2.По условию гипотезы равновозможны, следовательно, их вероятности равны

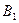Р(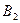)=Р()=Р()= .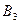

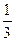3. Найдем условные вероятности события А при этих гипотезах:

; ; .

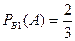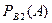
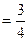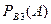
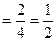4. Так как гипотезы 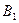, 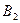и 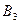- несовместны и образуют полную группу, то для расчета требуемой вероятности события А применима формула полной вероятности:

.

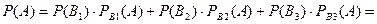
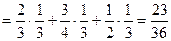5. Вероятность того, что белый шар вытащен из второй урны, рассчитаем по формуле Байеса:

.

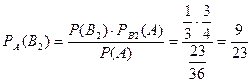I. В математической статистике имеется два способа оценки параметров статистических распределений:

- точечный, который указывает лишь точку, около которой находится неизвестный оцениваемый параметр (математическое ожидание, дисперсия);

- интервальный, когда находят интервал, в котором с некоторой, как правило с большой (выбираемой самим исследованием), вероятностью находится неизвестное значение параметра.

На практике часто приходится на основе результатов исследований (испытаний, экспериментов) проверять различные предположения (гипотезы) о характеристиках конкретного массового явления. Проверку гипотез на основе выборочных статистических данных называют статистической проверкой гипотез. Одну из гипотез выделяют в качестве основной, а другую – в качестве альтернативной (конкурирующей). При проверке гипотез могут возникать два рода ошибок:

1) первого рода, состоящая в том, что отвергается основная гипотеза, когда на самом деле она верна;

2) второго рода, состоящая в том, что отвергается конкурирующая гипотеза, когда она верна.

Задача 10. Дано статистическое распределение (статистический ряд) возраста 11 испытуемых х: 16,17, 18, 19, 20, 21, 22, 23, 24, 25, 26 лет. Требуется найти точечные оценки математического ожидания и дисперсии статистического распределения.

Решение: 1. Точечная оценка математического ожидания находится по формуле:

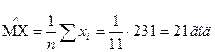
2. Точечная оценка дисперсии (несмещенная, состоятельная и эффективная) определяется по формуле:

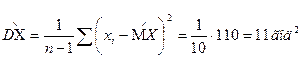
Задача 11. Дана выборка (статистический ряд) объёма n=9, точечные оценки 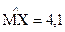и среднего квадратического отклонения 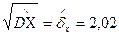. Требуется с доверительной вероятностью Р_д = 0,95 определить доверительный интервал, в котором находится искомое значение МХ.

Решение: 1. Для значений Р_д = 0,95 и k = n - 1 = 8 по таблице значений коэффициентов Стьюдента (табл. П3) находят значение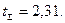

2. По формуле 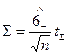находят меру точности определения МХ с помощью оценки .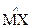

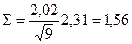3. В соответствии с неравенством 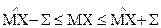определяют доверительный интервал

,

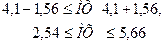то есть с доверительной вероятностью Р_д = 0,95 искомое значение МХ = 2,54…5,66.

Задача 12. В результате 15 независимых измерений давления найдена точечная оценка дисперсии 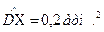. Требуется с доверительной вероятностью Р_д = 0,95 определить доверительные границы дисперсии DX.

Решение: 1. Расчет значения: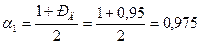

и значения: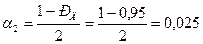

2. по таблице Х² – распределения (табл. П4) находят критические точки для

k = n-1 = 15-1 = 14 X²₁ = 5,63 Х²₂ = 26,1.

3. по таблице коэффициентов 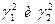(табл. П5) находят для Р_д = 0,95 и k = n-1 = 14 значения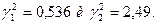

4. Устанавливают значения доверительных границ дисперсии

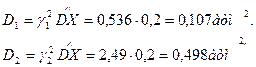
т.е. с вероятностью Р_д = 0,95 имеет место неравенство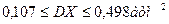

Задача 13. Дана выборка знаний случайной величины Х N = 100

1,09 1,25 1,19 1,31 1,30 1,05 1,27 1,45 1,31 1,30

1,56 1,36 1,16 1,37 1,11 1,58 1,32 1,48 1,39 1,41

1,58 1,46 1,30 1,36 1,30 1,56 1,12 1,32 1,35 1,34

1,31 1,21 1,29 1,29 1,30 1,30 1,24 1,38 1,27 1,30

1,50 1,34 1,46 1,33 1,17 1,30 1,31 1,45 1,33 1,18

1,31 1,20 1,41 1,38 1,27 1,29 1,20 1,42 1,38 1,39

1,25 1,14 1,34 1,28 1,33 1,39 1,14 1,44 1,38 1,43

1,23 1,26 1,26 1,35 1,22 1,43 1,30 1,26 1,35 1,50

1,46 1,30 1,30 1,27 1,24 1,18 1,28 1,29 1,44 1,25

1,36 1,18 1,36 1,22 1,21 1,38 1,16 1,36 1,24 1,19

Требуется используя критерий согласия Х², проверить гипотезу о законе распределения случайной величины Х на уровне значимости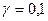

Решение: 1. Построение вариационного ряда результаты измерений располагают в порядке возрастания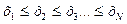

2. Вычисление размаха варьирования широты распределения:

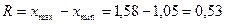
3. Определение числа разрядов g:

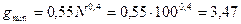
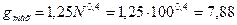
После округления g=3…8

Поскольку рекомендуется выбирать g нечетным и максимально большим, то принимают g = 7.

4. Определение ширины разряда:

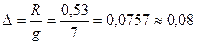
Правую границу последнего разряда принимают равный х_max, при этом ширина будет меньше, чем остальных.

5. Определение границ разрядов и числа n_i – количество результатов измерений, попадающих в каждый разряд (данные сводят в табл. 1)

Таблица 1.

Номер Разря-да j	Границы разряда	nj	Pj	NPj	(nj-NPj)^2
xj	xj+1
	1,05	1,13		0,1117	11,17	51,40	4,60
	1,13	1,21		0,1366	13,66	2,75	0,20
	1,21	1,29		0,1960	19,60	0,16	0,01
	1,29	1,37		0,2148	21,48	2,10	9,78
	1,37	1,45		0,1698	16,98	0,96	0,06
	1,45	1,53		0,1043	10,43	5,90	0,56
	1,53	1,58		0,0668	6,68	7,18	1,07
	-	-				-

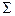
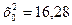
6. Построение гистограммы по полученным значениям n_i. При этом масштабом частости (или частоты 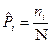) должна быть не высота, а площадь соответствующего прямоугольника, в то время как масштаб величины Х- линейный. Целесообразно, чтобы высота гистограммы относилась к основанию как 1:2 или 2:3

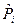_{0,36 0,28 0,20 0,12   0,04   1,05 1,13 1,21 1,29 1,37 1,45 1,53 1,58 Х}

По виду гистограммы выдвигают гипотезу Н₀ о нормальном законе распределения случайной величины Х.

7. Определение теоретических вероятностей Р_i попадания случайной величины Х в заданные разряды для чего:

- вычисляют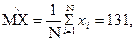

- вычисляют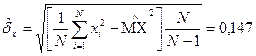

- определяют теоретические вероятности Р_i по падания случайной величины Х в интервалы

,

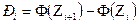где Z_i, Z_i+1 – концы выбранных интервалов выраженные через параметр Z функций Лапласа (табл. П2):

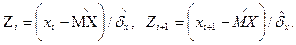
Результаты вычислений сводят в табл. 2, при этом наименьшее значение Z заменяют на 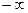, а наибольшее на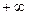

Таблица 2.

i	Границы разряда	Zi	Zi+1	Ф(Zi)	Ф(Zi+1)	Pi
xi	xi+1
	1,05	1,13		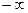-1,22	-0,5000	-0,3883	0,1117
	1,13	1,21	-1,22	-0,68	-0,3883	-0,2517	0,1366
	1,21	1,29	-0,68	-0,14	-0,2517	-0,0557	0,1960
	1,29	1,37	-0,14	0,41	-0,0557	0,1591	0,2148
	1,37	1,45	0,41	0,95	0,1591	0,3289	0,1698
	1,45	1,53	0,95	1,50	0,3289	0,4332	0,1043
	1,53	1,58	1,50		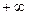0,4332	0,5000	0,0668

Значения функции Ф(Z) приведены в табл. П.2.

8. Определение числа степеней свободы K = g – S – 1. Для нормального закона S = 2, -т.к. он характеризуется двумя параметрами МХ и DX. Тогда k = 7 – 2 – 1 = 4.

8. Для k = 4 и заданного по табл.П 4находят точку распределения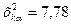

9. Так как , то гипотезу о нормальном распределении случайной величины Х отвергают.

II. Корреляционный анализ является инструментом исследования на основе выборочных данных статистической взаимозависимости ряда величин, некоторые из которых являются случайными. Исследование зависимости случайной величины от ряда неслучайных и случайных величин приводит к моделям регрессии т регрессионному анализу на основе выборочных данных. Метод наименьших квадратов используют с целью определения зависимости одной величины от другой и представлении полученных результатов в виде аналитического выражения, наиболее точно отражающего искомую зависимость.

Задача 14. Даны результаты измерения двух случайных величин:

x	2,21	0,09	0,03	0,61	0,75	2,18	1,87	1,27	1,12	-0,85
y	1,19	0,77	-0,63	-0,46	1,31	3,03	2,30	2,11	-0,31	0,52

Требуется: 1). построить поле корреляции, т.е. y = f(x); 2). определить и построить линейные уравнения регрессии; 3). определить оценку коэффициента корреляции между результатами измерения двух случайных величин x и y; 4). определить интервальную оценку коэффициента корреляции.

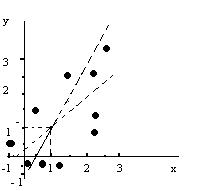Решение: 1. Построение поля корреляции (рис)

2. Определение оценок математических ожиданий.

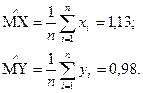
3. Определение оценок дисперсии:

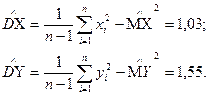
4.Определение оценки центрального момента

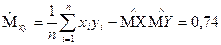
5. Определение линейных уравнений регрессии:

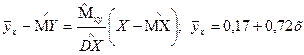
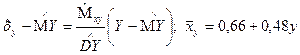
6. Определение интервальной оценки коэффициента корреляции с использованием критерия Фишера:

7. Определение интервальной оценки коэффициента корреляции с использованием критерия Фишера:

1). (значение 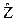может быть взято из табл.П6);

2). определение СКО случайной величины Z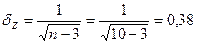

3). для нормального закона распределения случайной величины 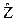, имеющей 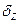, доверительный интервал 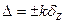, где в зависимости от доверительной вероятности Р_Д величина K принимает значения:

РД	0,680	0,870	0,900	0,950	0,997	0,999
К	1,00	1,50	1,65	2,00	3,00	4,00

4). задавая Р_Д = 0,9, получают 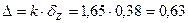и с доверительной вероятностью Р_Д = 0,9 величина Z может принять значения

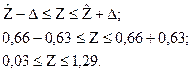
5). по табл. П6, по крайним значениям Z, находят левую и правую границы доверительного интервала коэффициента корреляции

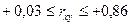
Задача 15. Даны результаты измерения двух случайных величин:

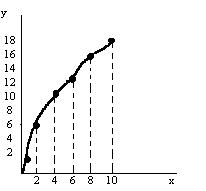
Х	0,5	2,0	4,0	6,0	8,0	10,0
y	1,7	5,8	9,7	12,1	15,3	17,8

Требуется: 1). определить вид уравнения, которому соответствуют результаты измерения X и Y; 2). определить наиболее вероятные коэффициенты искомого уравнения.

Решение: 1. Построение графика зависимости y = f(x). По виду графика предполагают, что искомая функциональная зависимость имеет вид y = ax^В. (рис.1.)

2. Для проверки выдвинутой гипотезы о виде функциональной зависимости логарифмируют уравнение у = ах^В

lg y = lg a + b lg x.

Обозначив У = lg y, А = lg a, X = ld x, получают уравнение У = А + bx.

2.

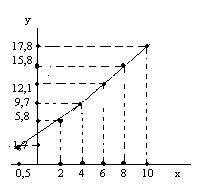Нанесение экспериментальных данных на логарифмическую сетку, для чего:

Рис.2

1).выбирают длину шкал по осям x и y: L_x = 100мм, L_y = 100 мм;

2). определяют масштабы по осям:

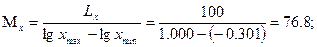
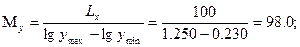
3). определение длин отрезное для соответствующих результатов измерений:

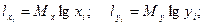
4) Результаты расчетов сводят в таблицу:

х	х = lgx		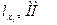	y	y = lgy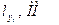
0,5	-0,301	-23,1		1,7	0,230	22,5
2,0	0,301	23,1		5,8	0,763	74,8
4,0	0,602	46,2		9,7	0,987	96,8
6,0	0,778	59,8		12,1	1,083	106,1
8,0	0,903	69,4		15,3	1,185	116,2
10,0	1,000	76,8		17,8	1,250	122,5

По данным таблицы строят зависимость Y = f(x) на функциональной (логарифмической) сетке, Рис.2.

5). поскольку на графике Y = f(x) данные измерений распространяются вокруг прямой линии, последовательно, предположение об искомой функциональной зависимости вида

у = ах^b справедливо.

4. Используя метод наименьших квадратов для уравнения У = А+bX, определяют наиболее вероятные значения коэффициентов А и В. Для этого определяют минимум суммы квадратов

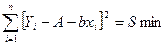
путем дифференцирования суммы квадратов сначала по А, а затем b и получают два уравнения: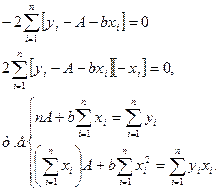

5. Решают полученную систему уравнений и получают значения параметров а и b:

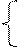6А + 3,288в = 5,498;

3,283А + 2,964и =3,916,

в = 0,78, А = 0,489, а = 3,08.

Следовательно, искомое уравнение имеет вид

у = 3,08 х^0,78.

Дата добавления: 2014-11-08