Директориальное свойство эллипса и гиперболы

Парабола

О п р е д е л е н и е. Параболой называется множество всех точек плоскости, расстояние от которых до заданной прямой, называемой директрисой, равно расстоянию до заданной точки – фокуса: .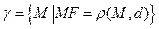

Расстояние 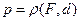от фокуса до директрисы называется фокальным параметром параболы.

По аналогии с эллипсом и гиперболой выводится каноническое уравнение параболы: .

Изучение формы параболы

1. 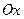– ось симметрии параболы.

2. Точки принадлежат параболе.

3. Поиск точек пересечения произвольной прямой проходящей через начало системы координат 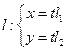с параболой сводится к решению к решению уравнения . Таким образом, если прямая 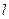отлична от оси 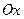(), то она пересекает параболу в двух различных точках. Ось 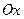пересекает параболу в одной точке.

О п р е д е л е н и е. Директрисой эллипса (гиперболы) называется прямая, перпендикулярная фокальной оси и отстоящая от второй оси на расстоянии .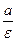

Таким образом, для эллипса (гиперболы), заданных каноническими уравнениями 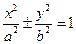, директрисы задаются уравнениями .

Имеет место следующая теорема

Т е о р е м а. Эллипс (гипербола) есть множество всех точек плоскости, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.

Д о к а з а т е л ь с т в о.Фактически требуется доказать совпадение двух множеств: эллипса (гиперболы) и множества точек, обладающих указанным в теореме свойством. Таким образом, достаточно показать включение каждого из этих множеств в другое.

1. Для любой точки 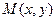, принадлежащей эллипсу (гиперболе), её координаты удовлетворяют уравнению 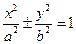. Кроме того, для этих линий соответственно имеем соотношения: . Учитывая это, можно подсчитать 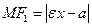. Так как , то получаем . Таким образом, имеет место включение всех точек эллипса (гиперболы) во множество точек, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету.

2. Пусть для точки 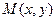имеет место равенство . Получаем 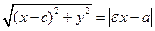или

.(*)

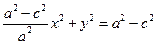Если 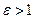, то и 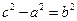. Уравнение (*) определяет гиперболу 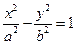. То есть точка 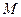принадлежит гиперболе.

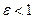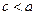Если , то , и уравнение (*) определяет эллипс 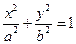. То есть точка 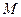принадлежит эллипсу.

Таким образом, для множества точек, отношение расстояний от которых до фокуса к расстоянию до соответствующей директрисы равно эксцентриситету, показали его включение во множество точек эллипса (гиперболы).

Из пунктов 1, 2 следует справедливость утверждения теоремы.

Лекция 5. Классификация линий второго порядка на плоскости

Дата добавления: 2014-11-20