Приведение общего уравнения линии второго порядка к каноническому виду

Из определения алгебраической линии следует, что в произвольной аффинной системе координат 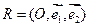уравнение линии второго порядка имеет вид:

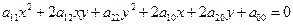, (1)
где 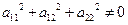– общее уравнение алгебраической линии второго порядка.

Пусть относительно прямоугольной системы координат 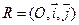линия второго порядка задана уравнением (1).

Т е о р е м а. Для каждой линии второго порядка, заданной в прямоугольной системе координат уравнением (1), существует прямоугольная система координат 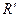, в которой линия задается уравнением вида

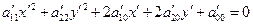(2).

Д о к а з а т е л ь с т в о. Имеем формулы преобразования координат при повороте осей координат на угол

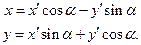(3)

Чтобы найти уравнение линии в новой системе координат, нужно в уравнение (1) подставить выражения (3) старых координат через новые. Будем искать такой угол поворота осей координат, чтобы в новом уравнении коэффициент при 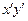был равен нулю:

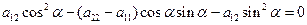. (4)

В уравнении (4) 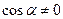. В противном случае, получим 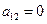, то есть уравнение (1) уже имеет требуемый вид.

Из однородного уравнения (4) находим два значения угла , для которых коэффициент при произведении текущих координат обращается в нуль. Можно выбрать любой из них. При повороте осей координат системы 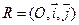на этот угол получим искомый репер .

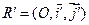Пусть уравнение линии второго порядка приведено к виду (2). Возможны случаи

I. .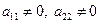

Выделив для и 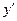полные квадраты, получим уравнение вида

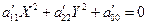, (5)

где обозначено

Отсюда получаем 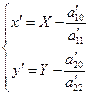– формулы преобразования координат при переносе начала системы координат в точку .

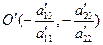В зависимости от значений параметров 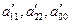можно получить следующие канонические уравнения

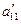
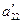
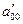
			Каноническое уравнение	Название линии
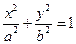
+	+	-		Эллипс
-	-	+
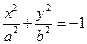
+	+	+		Мнимый эллипс
-	-	-
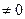
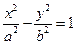
+	-			Гипербола
-	+
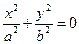
+	+			Пара мнимых пересекающихся прямых
-	-
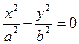
+	-			Пара пересекающихся прямых
-	+

II. .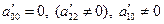

Уравнение (2) можно записать в виде

.

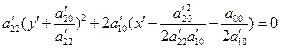Обозначив 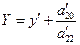, , 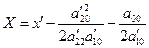получим каноническое уравнение параболы: .

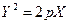III. .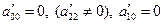

Уравнение линии приводится к виду 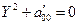. В зависимости от значений параметра 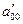получаем каноническое уравнение пары параллельных прямых, пары совпавших прямых, пары мнимых параллельных прямых.

Таким образом, имеем 9 сортов линий второго порядка.

Чтобы привести уравнение линии второго порядка к каноническому виду, надо:

1. добиться, чтобы в группе старших членов исчез член с произведением текущих координат (поворот осей координат);

2. добиться, чтобы число членов первой степени стало наименьшим (выделение полных квадратов, перенос начала системы координат);

3. если возможно, уничтожить свободный член (перенос начала системы координат).

Дата добавления: 2014-11-20