Реализация решения в Excel

Решение

Пусть х₁, х₂, х₃ – количество контейнеров, тогда затраты времени и ограничения на погрузку на первой, второй, третьей операции составят соответственно

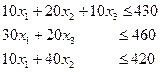
При этом х₁, х₂, х₃ ≥ 0.

Прибыль от перевозки контейнеров (целевая функция)

f(x) = 300х₁+200х₂+500х₃ → maх

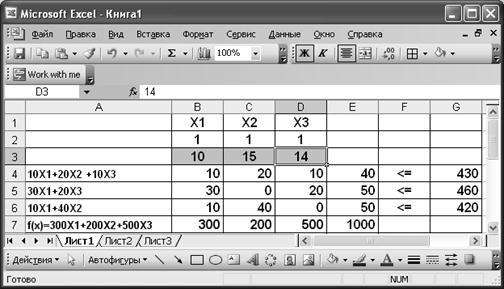
Положим х₁ = х₂ = х₃ = 1 (содержимое ячеек B2, C2, D2). Эти значения будут изменены в процессе использования встроенного модуля «Поиск решения», поэтому какие значения выбрать в качестве опорного плана - неважно. Итак, на первом скриншоте представлены данные по условию задачи.

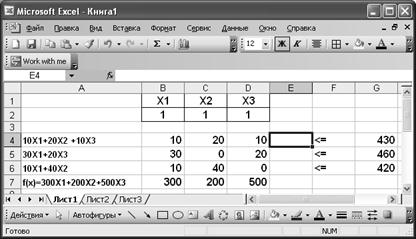
Вычислим затраты времени на погрузку по каждому виду операций, т.е.фактически вычисляем левые части системы ограничений при х₁=х₂=х₃=1. Для вычислений используем встроенную в Excel математическую функцию СУММПРОИЗВ, а также применяем абсолютные ссылки в Excel.

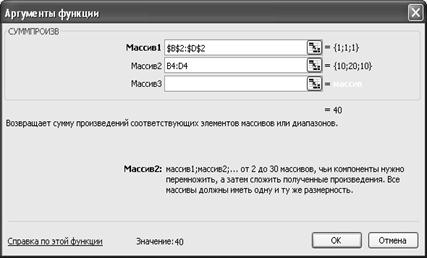
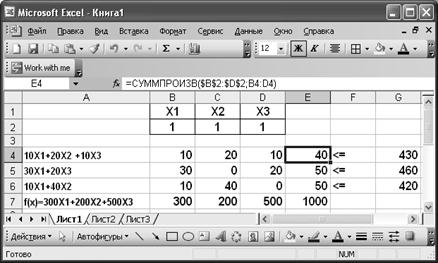
Итак, теперь в диапазоне B2:D2 – изменяемые значения, в Е4:Е6 – затраты времени на погрузку по операциям, в G4:G6 – ограничения по времени на работу оборудования, в Е7 – прибыль от погрузки контейнеров (целевая функция). Открываем модуль и заполняем его: Сервис \ Поиск решения

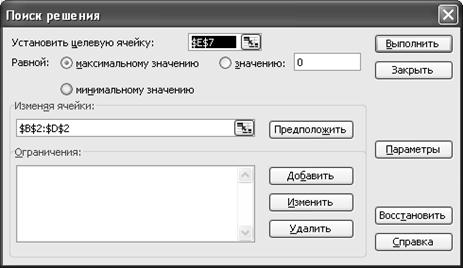
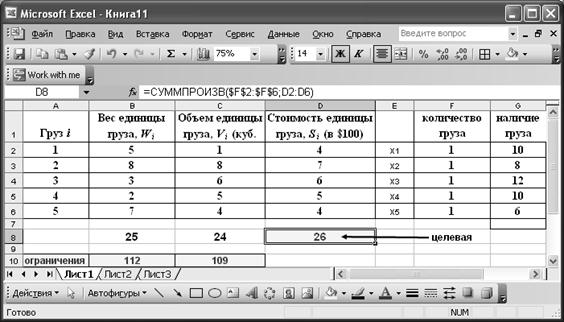
В окне «Добавление ограничения» пропишем ограничения на переменные и ресурсы:

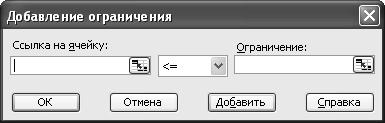
Окончательно окно «Поиск решения» примет вид:

Заметим, что внесенные данные, в том числе по ограничениям, в любой момент можно изменить или удалить.

Итак, целевая ячейка определена, изменяемые ячейки внесены, ограничения записаны. Нажмем кнопку «Выполнить».

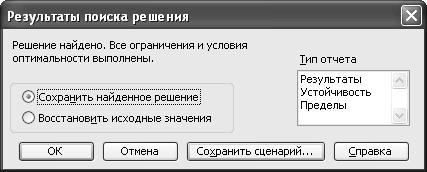
В случае, если задача поставлена некорректно или математическая модель составлена неверно (противоречива система ограничений), «Поиск…» выдает соответствующее диалоговое окно «Поиск не может найти решение».

Если все было выполнено верно, в изменяемых и расчетных ячейках окна Excel появится оптимальный результат:

Таким образом, оптимальное решение: перевозка контейнеров первого типа – нерентабельна, контейнеров второго типа требуется перевезти 10 единиц, контейнеров третьего типа 23 единицы. При этом максимальная прибыль от перевозки груза составит $13500.

Допустим, поступили дополнительные сведения о количестве готовых к погрузке контейнеров: пусть контейнеров первого типа имеется 10 штук, второго 15 и третьего 14. Принять управленческое решение в изменившихся условиях.

Решение. В системе ограничений требуется добавить: :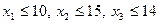

Новое ограничение появилось в окне ограничений.

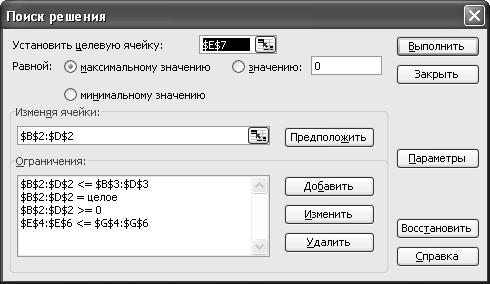
Тогда оптимальный план загрузки, максимизирующий прибыль с учетом ограничений,

Оптимальное решение: контейнеров первого типа требуется перевезти 6 единиц, контейнеров второго типа 9 единиц, контейнеров третьего типа 14 единиц. При этом максимальная прибыль от перевозки груза составит $10600. (Очевидно, дополнительное ограничение уменьшило значение целевой функции).

Таким образом, мы можем принимать наилучшее (оптимальное) управленческое решение в любых изменяющихся реальных условиях (если задача поставлена корректно!)

Задача №2 ( Задача о загрузке)

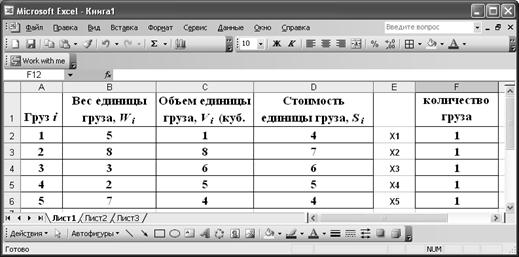
Подготовлены к погрузке на паром грузы пяти типов. Вес W_i, объем V_i, a также стоимость S_i, единицы груза каждого типа приведены в следующей таблице.

Груз i	Вес единицы груза, Wi (тонны)	Объем единицы груза, Vi (куб. ярд)	Стоимость единицы груза, Si (в $100)

Максимальная грузоподъемность и объем парома равны 112 тонн и 109 куб. яр­дов соответственно. Построить оптимальный план погрузки, обеспечивающий максимальную стоимость груза.

Решение. Сначала построим математическую модель задачи.

Пусть х₁, х₂, х₃, х₄, х₅ – количество грузов каждого типа, тогда ограничения на погрузку по весу и объему составят соответственно

При этом х₁, х₂, х₃, х₄, х₅ ≥ 0.

Прибыль от перевозки грузов (целевая функция)

f(x) = 4х₁ + 7х₂ + 6х₃ + 5х₄ + 4х₅ → maх

Реализация решения в Excel. Аналогично тому, как было выполнено в первой задаче,определим изменяемые ячейки,целевую ячейку иограничения на вес и объем перевозимого груза.

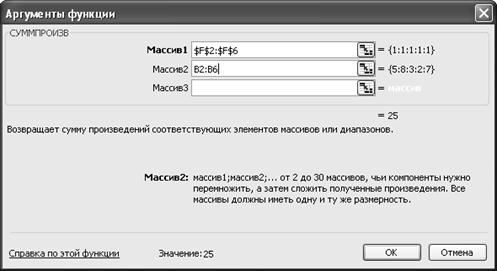
Теперь заполним модуль «Поиск решения».

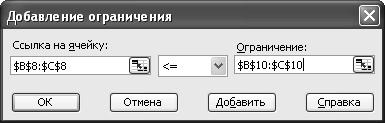
Нажмем кнопку «Выполнить и получим оптимальное решение поставленной задачи.

В изменяемых ячейках появятся допустимые (т.е. удовлетворяющие системе ограничений) значения переменных (количество груза каждого типа), при которых целевая функция (прибыль) достигает максимального значения.

Таким образом, наибольшая прибыль соответствует перевозке 14 единиц 1-го груза и 19 единиц 4-го груза.

Допустим, что количество имеющегося для отправки груза ограничено (значения в диапазоне G2:G6):

Для принятия управленческого решения в изменившихся условиях добавим ограничение в окно ограничений модуля «Поиск решений»:

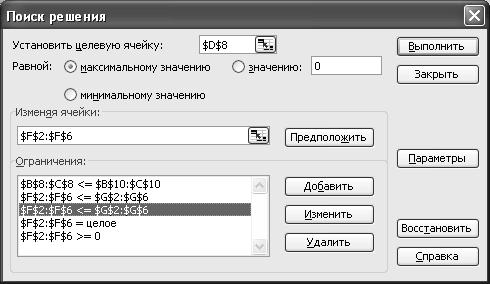
Тогда после нажатия на кнопку «Выполнить» получим оптимальное решение:

Итак,для получения максимальной прибыли при соблюдении ограничений на вес и объем груза требуется взять на борт 10 единиц 1-го груза, 11 – третьего, 5 – четвертого и 2 – пятого груза.

Варианты заданий по теме «Решение оптимизационных задач средствами Excel»

Цель работы: Изучить возможности Excel для решения оптимизационных задач.

Задание

1. Для каждой из предложенных задач построить математическую модель.

2. Получить оптимальное решение.

3. В документе Microsoft Word составить отчет о работе.

Задача №1

Для сохранения нормальной жизнедеятельности человек должен в сутки потреблять белков не менее 120 условных е`диниц (усл.ед.), жиров - не менее 70 и витаминов - не менее 10 усл.ед. Содержание их в каждой единице продуктов и 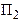равно соответственно (0,2; 0,075; 0) и (0,1; 0,1; 0,1) усл.ед. Стоимость 1 ед. продукта - 20 грн, 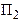- 30 грн.

Постройте математическую модель задачи, позволяющую так организовать питание, чтобы его стоимость была минимальной, а организм получил необходимое количество питательных веществ.

Задача №2

С вокзала можно отправлять ежедневно курьерские и скорые поезда. Вместимость вагонов и наличный парк вагонов на станции указаны в таблице.

Дата добавления: 2014-11-08