Методи урахування податків і інфляції

У розглянутих вище методах визначення нарощеної суми не враховувались такі важливі моменти як податки й інфляція. Розглянемо цю проблему.

У ряді країн одержані (юридичними, а іноді й фізичними особами) відсотки обкладаються податком, що, природно, зменшує реальну нарощену суму і доходність операції.

Позначимо нарощену суму до сплати податків через S, а з урахуванням їх сплати як S ^/. Нехай ставка податку на відсотки дорівнює g, а загальна сума податку G.

При нарахуванні простих відсотків за весь рік знаходимо:

(4.3)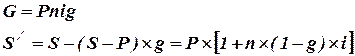

Таким чином урахування податку при визначенні нарощеної суми зводиться до відповідного скорочення відсоткової ставки – замість ставки і фактично застосовується ставка 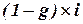. Розмір податку пропорційний строку. Перейдемо до довгострокових операцій зі складними відсотками:

(4.4)

Нехай ставка податку на відсотки дорівнює 10%. Відсоткова ставка – 30% річних, строк нарахування відсотків – 3 роки. Першочергова сума позики 1000 тис. грн.. Визначимо розміри податку при нарахуванні простих і складних відсотків. При нарахуванні простих відсотків одержимо наступні показники: 1900 тис. грн. без сплати податку, S^/ = 1000(1+3(1-0,1)0,3) = 1810 тис. грн. з урахуванням сплати податку. Нарахуємо тепер складні відсотки: 2197 тис. грн. без сплати податку, S^/ = 1000((1-0,1)(1+0,3)^3+0,1) = 2077,3 тис. грн.. з урахуванням сплати податку.

У розглянутих вище методах нарощення всі грошові величини вимірювались за номіналом. Інакше кажучи, не приймалось до уваги зниження реальної купівельної спроможності грошей за період, який охоплює операція. Однак у сучасних умовах інфляція у грошових відносинах відіграє помітну роль, і без її урахування кінцеві результати часто представляють собою умовну величину.

Інфляцію необхідно враховувати по крайній мірі в двох випадках: при розрахунку нарощеної суми грошей і при зміні реальної ефективності (доходності) фінансової операції.

Неважко зв’язати індекс цін і темп інфляції. Під темпом інфляції h розуміють відносний приріст цін за період (звичайно він вимірюється у відсотках):

(4.5)

, де – індекс цін.

Інфляція є ланцюговим процесом. Отже, індекс цін за декілька періодів рівний добутку ланцюгових індексів цін:

(4.6)

, де – темп інфляції в періоді t.

Нехай тепер мова йде про майбутнє. Якщо h – постійний очікуваний (або прогнозований) темп інфляції за один період, то за п таких періодів отримаємо:

(4.7)

.

Грубою помилкою, яка, нажаль, зустрічається у вітчизняній практиці, є сумування темпів інфляції окремих періодів для одержання узагальнюючого показника інфляції за весь термін. Що, відмітимо, суттєво занижує величину одержаного показника.

Постійний темп інфляції на рівні 5% на місяць призводить до зростання цін за рік у розмірі 1,05^12=1,796. Таким чином, дійсний річний темп інфляції рівний 79,6%, а не 60% як при сумуванні. Продовжимо приклад. Нехай прирости цін за 3 місяці склали: 1,5; 1,2 та 0,5%. Індекс цін за три місяці рівний 1,015*1,012*1,005=1,0323. Темп інфляції за три місяці – 3,23%.

Повернемось до проблеми знецінення грошей при їх нарощенні. Якщо нарощення відбувається за простою ставкою, то нарощена сума з урахуванням купівельної спроможності рівна:

(4.8)

.

Як бачимо, збільшення нарощеної суми з урахуванням її інфляційного знецінення має місце лише коли .

На суму 1,5 млн. грн. на протязі трьох місяців нараховуються прості відсотки за ставкою 28% річних, нарощена сума, отже, рівна 1,605 млн. грн.. Щомісячна інфляція характеризується темпами 2,5; 2,0 і 1,8%. Індекс цін рівний 1,025*1,02*1,018=1,06432. З урахуванням знецінення нарощена сума складе: 1,605/1,06432=1,508 млн. грн..

Звернемось тепер до нарощення за складними відсотками. Нарощена сума з урахуванням інфляційного знецінення знаходиться як:

(4.9)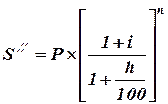

.

Очевидно, що при нарахуванні простих відсотків ставка, яка компенсує вплив інфляції, відповідає величині:

(4.10)

.

Ставку, що перевищує критичне значення і^/ (при нарахуванні складних відсотків i^/=h), називають позитивною ставкою відсотку

.Власники коштів, звісно, не можуть змиритись із їх інфляційним знеціненням і здійснюють різні спроби компенсації втрат.

Найбільш розповсюдженим є коригування ставки відсотку, за яким відбувається нарощення, тобто збільшення ставки на величину так званої інфляційної премії. Підсумкову величину можна назвати брутто-ставкою.

Дата добавления: 2014-11-20