Билет 7

Нулевым является вектор, имеющий нулевую длину, то есть тот, у которого координаты начала и конца строго совпадают. В связи с этим обычно нельзя говорить о направлении такого вектора, поэтому его считают не имеющим направления.

Ответ: в геометрическом смысле вектор — это направленный отрезок, обычно определяемый точками своего начала и конца. Так или иначе вектором - называется отрезок, имеющий определенную длину и направление

Билет

1. Вектор. Понятия

Основные понятия

1) Модулем вектора |a| в геометрии называется его длина

2) Коллинеарными называются такие вектора, векторное произведение которых равно нулю. Это параллельные вектора. Коллинеарные вектора могут быть сонаправленными или встречными, то есть направленными строго в противоположные стороны.

3) Ортогональными (перпендикулярными) называются такие вектора, скалярное произведение которых равно нулю. Для любого вектора все вектора, лежащие в любой перпендикулярной ему плоскости, будут ортогональны.

5) Компланарными называются вектора, которые приведены к одному началу и лежат в одной плоскости. Если хотя бы один из 3 векторов – нулевой, то три вектора тоже компланарны.

6) Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

7) Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.

2. Сумма векторов и произведение вектора на число.

Ответ: начнем с простого, чтобы сложить два вектора, достаточно сложить каждую из его координат. Т.е. если есть два вектора с координатами: a (x y z) u b (x1 y1 z1) то их суммой будет:

(x+x1;y+y1;z+z1). С этим ясно, умножение вектора на число тоже довольно просто. Если есть вектор a(x y z) и число b=4, то просто домножаем КАЖДУЮ координату на это число.

3. Условие коллинеарности векторов:

Ответ:

1) Два вектора коллинеарны, если их отношения равны

2) Два вектора коллинеарны, если их векторное пр-е равно нулю.

Пример внизу.

4. Свойства линейных операций над векторами

Сложение векторов коммутативно: .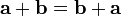

Сложение векторов ассоциативно: .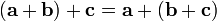

Прибавление нулевого вектора к любому не меняет последнего: .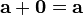

Для любого вектора 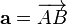существует вектор 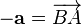такой, что 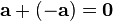или .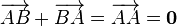

Умножение вектора на число ассоциативно: 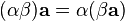. Умножение вектора на число дистрибутивно относительно сложения чисел: .

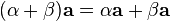Дистрибутивность умножения векторов относительно сложения

Умножение вектора на число дистрибутивно относительно сложения векторов: .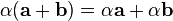

Очевидно, умножение на единицу не меняет вектор: .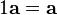

1. Базис и система координат на плоскости и в пр-ве

Ответ: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов 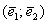, взятых в определённом порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов.

Любой вектор плоскости 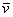единственным образом раскладывается по базису :
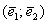, где 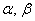– действительные числа. Числа 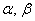называют координатами вектора в данном базисе.

Также говорят, что вектор 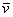представлен в виде линейной комбинации базисных векторов. То есть, выражение 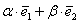называют разложением вектора 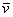по азису 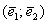или линейной комбинацией базисных векторов.

Иными словами, говоря о разложении по базису мы подразумеваем какие-то коэффициенты, которые соответствуют векторам.

1.1 Система координат на плоскости

Ответ: Когда говорят о прямоугольной системе координат, то чаще всего имеют в виду начало координат, координатные оси и размерность по осям. Прямоугольную систему координат вполне можно определить через ортонормированный базис 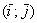. И это почти так. Формулировка звучит следующим образом:

Точка 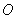плоскости, которая называется началом координат, и ортонормированный базис 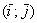задают декартову прямоугольную систему координат плоскости. То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами .

Думаю, всем понятно, что с помощью точки 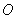(начала координат) и ортонормированного базиса 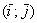ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».

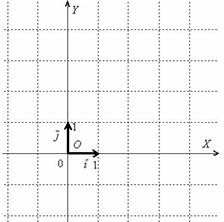
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку 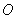и два ортогональных вектора 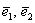произвольной ненулевой длины. Собственно пример данной системы, всем известной:

1.2. Система координат в пр-ве

Ответ: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов 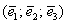, взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису 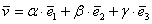, где 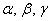– координаты вектора 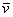в данном базисе

Напоминаю, также можно сказать, что вектор 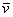представлен в виде линейной комбинации базисных векторов.

Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:

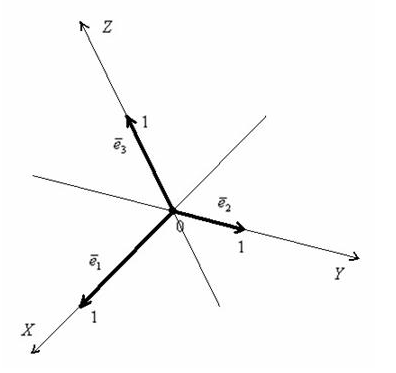
Точка 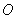пространства, которая называется началом координат, и некомпланарны е векторы 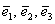, взятые в определённом порядке, задают аффинную систему координат трёхмерного пространства:

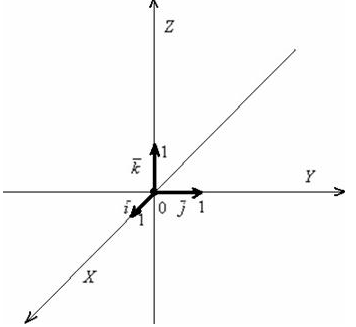
Точка пространства, которая называется началом координат, и ортонормированный базис задают декартову прямоугольную систему координат пространства.:

2. Геометрические и алгебраические проекции вектора на ось

3. Координаты вектора на плоскости и в пространстве

Начну с векторов на плоскости. Изображаем декартову с.к. и откладываем единичные вектора.

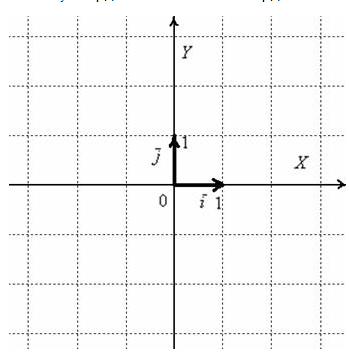
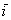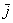Векторы и ортогональны. Ортогональны = Перпендикулярны.

Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: .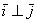

Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.

Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: 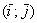. Координатные векторы нельзя переставлять местами.

Ответ: Любой вектор 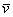плоскости единственным образом выражается в ви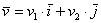де:
, где 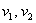– числа, которые называются координатами вектора в данном базисе. А само выражение 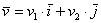называется разложением вектора 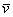по базису .

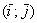Дата добавления: 2014-11-20