Модель матрицы доступов Харрисона-Руззо-Ульмана 3 страница

5. Каким может являться каждое состояние системы в соответствии с предложенным в модели критерием безопасности?

Лекция 5.

МОДЕЛЬ РАСПРОСТРАНЕНИЯ ПРАВ ДОСТУПА TAKE-GRANT

Основные положения классической модели Take-Grant

Классическая модель Take - Grant ориентирована на анализ путей распространения прав доступа в системах дискреционного управления доступом. Классическую модель Take - Grant будем рассматривать на основе [Девянин].

Основными элементами модели Take - Grant являются:

O ¾ множество объектов;

S Í O ¾ множество субъектов;

R = { r ₁, r ₂, …, r_m } È { t, g } ¾ множество видов прав доступа, где t (take) ¾ право брать права доступа, g (grant) ¾ право давать права доступа;

G = (S, O, E) ¾ конечный помеченный ориентированный без петель граф доступов, описывающий состояние системы. Элементы множеств S и O являются вершинами графа, которые будем обозначать, соответственно, Ä ¾ объекты (элементы множества O \ S), · ¾ субъекты (элементы множества S). Элементы множества E Í О ´ O ´ R являются ребрами графа. Каждое ребро помечено непустым подмножеством множества видов прав доступа R.

Состояние системы описывается соответствующим ему графом доступов. В отличие от модели ХРУ в модели Take-Grant возможно наличие прав доступа не только у субъектов к объектам, но и у объектов к объектам.

Основная цель классической модели Take-Grant ¾ определение и обоснование алгоритмически проверяемых условий проверки возможности утечки права доступа по исходному графу доступов, соответствующего некоторому состоянию системы.

Порядок перехода системы модели Take-Grant из состояния в состояние определяется правилами преобразования графа доступов, которые в классической модели носят название де-юре правил. Преобразование графа G в граф G ’в результате выполнения правила op обозначим через:

G ├ _op G ’.

В классической модели Take-Grant рассматриваются четыре де-юреправила преобразования графа, выполнение каждого из которых может быть инициировано только субъектом, являющимся активной компонентой системы (рис. 5.1-5.4):

- take ¾ брать права доступа,

- grant ¾ давать права доступа,

- create ¾ создавать новый объект или субъект, при этом субъект создатель может взять на созданный субъект любые права доступа (по умолчанию предполагается, что при выполнение правила create создается объект, случаи, когда создается субъект, оговариваются особо),

- remove ¾ удалять права доступа.

Рассмотрим условия применения де-юре правил в исходном состоянии G = (S, O, E) и результаты их применения в результирующем состоянии G ’= (S ’, O ’, E ’) (табл. 1.3).

Таблица 5.1. Де-юре правила классической модели Take-Grant

Правила	Исходное состояние G = (S, O, E)	Результирующее состояние G ’= (S ’, O ’, E ’)
take (a, x, y, z)	x Î S, y, z Î O, (x, y, { t }) Ì E, (y, z, b) Ì E, x ¹ z, a Í b	S ’ = S, O ’ = O, E ’= E È {(x, z, a)}
grant (a, x, y, z)	x Î S, y, z Î O, (x, y, { g }) Ì E, (x, z, b) Ì E, y ¹ z, a Í b	S ’ = S, O ’ = O, E ’= E È {(y, z, a)}
create (b, x, y)	x Î S, y Ï O, b ¹ Æ	O ’= O È { y }, если y субъект, то S ’ = S È { y }, иначе S ’ = S, E ’= E È {(x, y, b)}
remove (a, x, y)	x Î S, y Î O, (x, y, b) Ì E, a Í b	S ’ = S, O ’ = O, E ’= E \ {(x, y, a)}

В модели Take-Grant основное внимание уделяется определению условий, при которых в системе возможно распространение прав доступа для случая, когда не рассматриваются ограничения на кооперацию субъектов при передаче прав доступа, и случая, когда на кооперацию субъектов наложены ограничения. Рассмотрим данные случаи подробнее.

1. Условия передачи прав доступа при отсутствии ограничений на кооперацию субъектов

Данный случай характеризуется тем, что при передаче прав доступа не накладывается ограничений на кооперацию субъектов системы, участвующих в этом процессе.

Определение 5.1. Пусть x, y Î O ₀, x ¹ y ¾ различные объекты графа доступов G ₀= (S ₀, O ₀, E ₀), a Í R. Определим предикат can_share (a, x, y, G ₀), который будет истинным тогда и только тогда, когда существуют графы G ₁= (S _1, O _1, E ₁), …, G_N = (S_N, O_N, E_N) и правила op ₁, …, op_N такие, что G ₀├ _{op 1} G ₁├ _{op 2}… ├ _opN G_N и (x, y, a) Ì E_N, где N ³ 0.

Определение истинности предиката can_share (a, x, y, G ₀) непосредственно по определению является в общем случае алгоритмически неразрешимой задачей, так как требует проверки всех траекторий функционирования системы. По этой причине для проверки истинности предиката can_share (a, x, y, G ₀) следует определить необходимые и достаточные условия, проверка которых возможна. Решение данной задачи будет выполнено в два этапа. На первом этапе будут определены и обоснованы условия истинности предиката can_share (a, x, y, G ₀) для графов, все вершины которых являются субъектами, на втором этапе условия истинности предиката can_share (a, x, y, G ₀) будут определены и обоснованы для произвольных графов.

Определение 5.2. Пусть G = (S, S, E) ¾ граф доступов, все вершины которого являются субъектами. Говорят, что вершины графа доступов являются tg -связными или что они соединены tg -путем, если, без учета направления ребер, в графе между ними существует путь такой, что каждое ребро этого пути помечено t или g.

Теорема 5.1. Пусть G ₀= (S ₀, S ₀, E ₀) граф доступов, содержащий только вершины субъекты, x, y Î S ₀, x ¹ y. Тогда предикат can_share (a, x, y, G ₀) истинен тогда и только тогда, когда выполняются условия 1 и2.

Условие 1. Существуют субъекты s ₁, …, s_m Î S ₀:

(s_i, y, g _i ) Ì E ₀, где i = 1, …, m и a = g₁ È … È g _m.

Условие 2. Субъекты x и s_i являются tg -связными в графе G ₀, где i = 1, …, m.

Доказательство. Проведем доказательство теоремы для m = 1, так как схему доказательства для этого случая легко продолжить для случая m > 1.

При m = 1 условия 1 и 2 формулируются следующим образом.

Условие 1. Существует субъект s такой, что выполняется включение (s, y, a) Ì E ₀.

Условие 2. Субъекты x и s соединены tg -путем в графе G ₀.

Достаточность. Пусть выполненыусловия1 и 2. Доказательство проведем индукцией по длине tg -пути, соединяющего субъектов x и s.

Пусть N = 0. Тогда, x = s, (x, y, a) Ì E ₀и предикат can_share (a, x, y, G ₀) истинен.

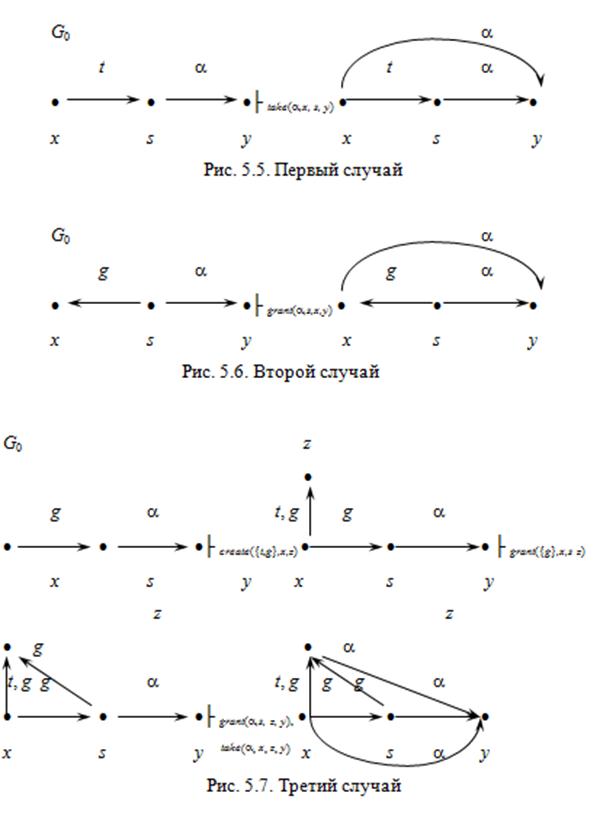
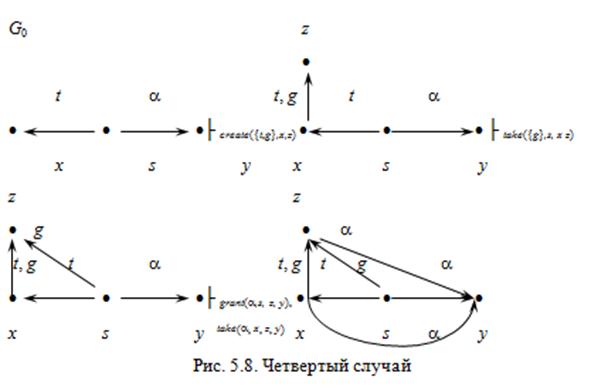
Пусть N = 1. Тогда существует (s, y, a) Ì E ₀, и x и s соединены ребром t или g в графе G ₀. Возможны четыре случая такого соединения x и s, для каждого из которых, указана последовательность преобразований графа, требуемая для передачи прав доступа (рис. 5.5-5.8).

Пусть длина пути N > 1. Пусть вершина z находится на tg- пути между x и s и является смежной с s в графе G ₀. Тогда исходя из доказанного для случая N = 1 существует последовательность преобразований графов доступов G ₀├ _{op 1} G ₁├ _{op 2}… ├ _opK G_K такая, что (z, y, a) Ì E_k, и длина tg- пути между z и x равна N – 1. Это позволяет применить предположение индукции. Достаточность условий теоремы доказана.

Необходимость. Пусть истинен предикат can_share (a, x, y, G ₀).

По определению истинности предиката существует последовательность графов доступов G ₁= (S ₁, O ₁, E ₁), …, G_N = (S_N, O_N, E_N) такая, что G ₀├ _{op 1} G ₁├ _{op 2}… ├ _opN G_N и (x, y, a) Ì E_N. Среди всех таких последовательностей выберем ту, у которой длина N является минимальной.

Докажем необходимость условий 1 и 2 индукцией по N.

При N = 0 очевидно, что (x, y, a) Ì E ₀. Таким образом, s = x и условиятеоремы выполнены.

При N = 1. Тогда выполняется условие (x, y, a) Ë E ₀, и из определения де-юреправил модели следует, что существует субъект s такой, что справедливо (s, y, a) Ì E ₀и или op ₁= take (a, x, s, y), или op ₁= grant (a, s, x, y). Таким образом, s и x являются tg -связными в графе G ₀и условия теоремы выполнены.

Пусть N > 1 и утверждение теоремы истинно для k < N. Тогда (x, y, a) Ë E_{N – 1}и ребро (x, y, a) появляется в графе доступов G_N в результате применения к графу G_{N –1} некоторого правила op_N. Очевидно, это не правила create или remove. Следовательно, существует субъект s ’Î S_{N – 1} такой, что (s ’, y, a) Ì E_{N - 1} и или (x, s ’, t) Î E_{N - 1} и op_N = take (a, x, s ’, y), или (s ’, x, g)Î E_{N –1} и op_N = grant (a, s ’, x, y).

Возможны два случая: s ’Î S ₀и s ’Ï S ₀.

Рассмотрим первый случай. Пусть s ’Î S ₀, тогда истинен предикат can_share (a, s ’, y, G ₀), при этом число преобразований графов меньше N. Следовательно, по предположению индукции существует s Î S ₀: (s, y, a) Î E ₀,и s ’соединен с s tg- путем в графе G ₀. Кроме того, если op_N = take (a, x, s ’, y), то истинен предикат can_share ({ t }, x, s ’, G ₀), а если op_N = grant (a, s ’, x, y), то истинен предикат can_share ({ g }, s ’, x, G ₀); при этом число преобразований графов меньше N. Следовательно, по предположению индукции существует s ’’Î S ₀, такой, что если op_N = take (a, x, s ’, y), то (s ’’, s ’, t) Î E ₀и s ’’соединен с x tg- путем в графе G _0, а если op_N = grant (a, s ’, x, y), то (s ’’, x, g) Î E ₀и s ’’соединен с s ’ tg- путем в графе G ₀. Таким образом, существует s Î S ₀: (s, y, a) Ì E ₀и субъекты x и s соединены tg- путем в графе G ₀. Для случая s ’Î S ₀индуктивный шаг доказан (рис. 5.9).

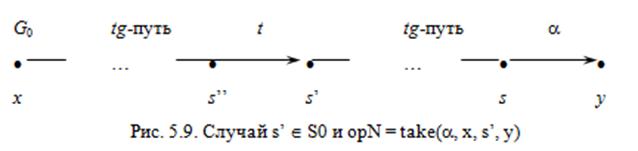
Рассмотрим второй случай. Пусть s ’Ï S ₀. Заметим, что число преобразований графов N минимально, поэтому преобразования графов удовлетворяют следующим требованиям:

- каждый субъект графа G ₀создает не более одного субъекта,

- субъект создатель берет на созданный субъект необходимый набор прав { t, g };

- созданный субъект не создает новых субъектов.

Справедливость перечисленных требований следует из того, что если субъект графа G ₀создает более одного субъекта или созданный субъект создаст нового субъекта, то в преобразованиях графов доступов такие дополнительные субъекты могут быть заменены имеющимися. Следовательно, не будет являться необходимым применение правил создания дополнительных субъектов, что противоречит условию минимальности числа преобразований графов. Требование к субъекту создателю брать на созданный субъект необходимый набор прав { t, g } является, очевидно, необходимым.

Из перечисленных требований следует, что существуют M < N – 1, s ’’Î S ₀: op_M = create ({ t, g }, s ’’, s ’). Среди всех последовательностей преобразований длины N можно выбрать такую, что M = 1. Тогда рассмотрим граф G ₁; при этом S ₁= S ₀È { s ’}, E ₁= E ₀È {(s ’’, s ’, { t, g })}, истинен предикат can_share (a, s ’, y, G ₁) с числом преобразований меньше N и s ’Î S ₁. Следовательно, существует s Î S ₁: (s, y, a) Ì E ₁, при этом s и s ’соединены tg -путем в графе G ₁. Очевидно, что s Î S ₀, (s, y, a) Ì E ₀; при этом s и s ’’соединены tg -путем в графе G ₀. Кроме того, если op_N = take (a, x, s ’, y), то истинен предикат can_share ({ t }, x, s ’, G ₁), а, если op_N = grant (a, s ’, x, y), то истинен предикат can_share ({ g }, s ’, x, G ₁); при этом число преобразований меньше N. Следовательно, так как s ’’единственный субъект в графе G ₁, обладающий правами доступа к субъекту s ’, то x и s ’’соединены tg -путем в графе G ₁и, соответственно, в графе G ₀.

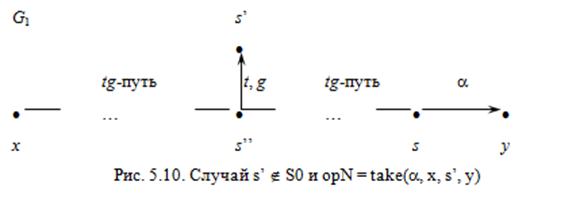
Таким образом, существует s Î S ₀: (s, y, a) Ì E ₀; при этом x и s соединены tg -путем в графе G ₀. Для случая s ’Ï S ₀индуктивный шаг доказан (рис. 5.10).

Теорема доказана. ■

Для определения истинности предиката can_share (a, x, y, G ₀) в произвольном графе дадим определения.

Определение 5.3. Островом в произвольном графе доступов G ₀называется его максимальный tg- связный подграф, состоящий только из вершин субъектов.

Определение 5.4. Мостом в графе доступов G ₀называется tg -путь, концами которого являются вершины субъекты, проходящий через вершины объекты, словарная запись которого имеет вид:

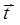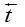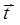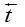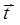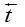^*, ^*, ^{* *}, ^{* *}, где символ «*» означает многократное (в том числе нулевое) повторение.

Определение 5.5. Начальным пролетом моста в графе доступов G ₀называется tg- путь, началом которого является вершина субъект, концом ¾ объект, проходящий через вершины объекты, словарная запись которого имеет вид: ^* .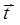

Определение 5.6. Конечным пролетом моста в графе доступов G ₀называется tg- путь, началом которого является вершина субъект, концом ¾ объект, проходящий через вершины объекты, словарная запись которого имеет вид: ^*.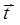

Теорема 5.2. Пусть G ₀= (S ₀, O ₀, E ₀) произвольный граф доступов, x, y Î O ₀, x ¹ y. Предикат can_share (a, x, y, G ₀) истинен тогда и только тогда, когда или (x, y, a) Ì E ₀, или выполняются условия1-3:

Условие 1. Существуют объекты s ₁, …, s_m Î O ₀:

(s_i, y, g _i) Ì E ₀для i = 1, …, m и a = g₁ È … È g _m.

Условие 2. Существуют субъекты x ₁’, …, x_m ’, s ₁’, …, s_m ’Î S ₀:

1) x = x_i ’или x_i ’соединен с x начальным пролетом моста в графе G ₀, где i = 1, …, m;

2) s = s_i ’или s_i ’соединен с s конечным пролетом моста в графе G ₀, где i = 1, …, m.

Условие 3. В графе G ₀для каждой пары (x_i ’, s_i ’), где i = 1, …, m, существуют острова I_{i ,1}, …, I_{i , ui}, u_i ³ 1, такие, что x_i ’Î I_{i ,1}, s_i ’Î I_{i , ui}, и существуют мосты между островами I_{i , j} и I_{i , j+ 1}, где j = 1, …, u_i – 1.

Доказательство. Проведем доказательство теоремы для m = 1, так как схему доказательства для этого случая легко продолжить на случай m > 1.

При m = 1 условия1-3 формулируются следующим образом (рис. 5.11).

Условие 1. Существует объект s Î O ₀: (s, y, a) Ì E ₀.

Условие 2. Существуют субъекты x ’, s ’Î S ₀:

1) x = x ’или x ’соединен с x начальным пролетом моста в графе G ₀;

2) s = s ’или s ’соединен с s конечным пролетом моста в графе G ₀.

Условие 3. В графе G ₀существуют острова I ₁, …, I_u, u ³ 1, такие, что x ’ Î I ₁, s ’ Î I_u, и существуют мосты между островами I_j и I_{j + 1}, где j = 1, …, u – 1.

Достаточность. Если (x, y, a) Ì E ₀, то предикат can_share (a, x, y, G ₀) истинен.

Пусть выполнены условия 1-3 теоремы. Является очевидным тот факт, что по мостам возможна передача прав доступа между субъектами, являющимися его концами. В качестве примера разобрана последовательность преобразований графа доступов при передаче прав по мосту вида 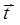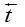(рис. 5.12).

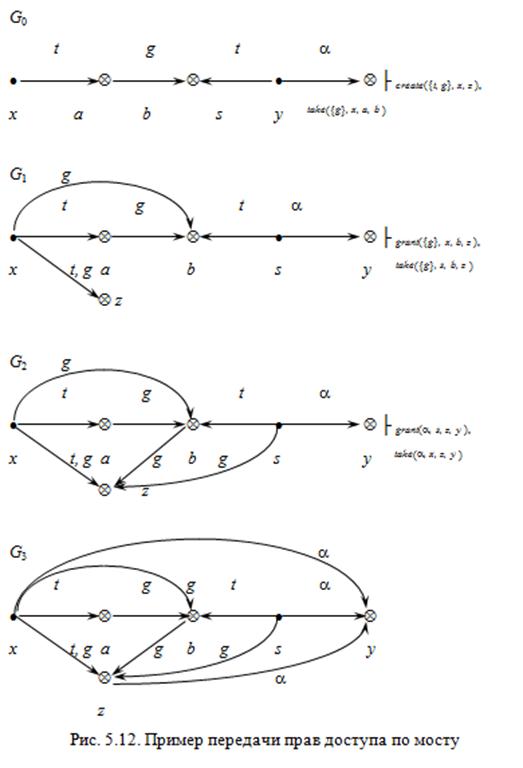
Также очевидно, что по конечному пролету моста субъект может забрать права доступа у объекта, а по начальному пролету ¾ передать их объекту.

По условию1 существует объект s, который обладает правами a к объекту у. По условию2(б) существует субъект s ’, который, либо совпадает с s, либо по конечному пролету моста может забрать у субъекта s права a к объекту у.

По теореме5.1 права доступа, полученные одним субъектом, принадлежащим острову, могут быть переданы любому другому субъекту острова. По условию3 между островами существуют мосты, по которым возможна передача прав доступа. По условию2(а) существует субъект x ’, который или совпадает с x, или, получив права доступа, может передать их x по начальному пролету моста.

Необходимость. Пусть истинен предикат can_share (a, x, y, G ₀). По определению истинности предиката существует последовательность графов доступов G ₁= (S ₁, O ₁, E ₁), …, G_N = (S_N, O_N, E_N) такая, что: G ₀├ _{op 1} G ₁├ _{op 2}… ├ _opN G_N и (x, y, a) Ì E_N; при этом N ³ 0 выбирается минимальным. Докажем необходимость выполнения условий теоремы индукцией по N.

При N = 0 очевидно, что (x, y, a) Ì E ₀. Следовательно, условиятеоремы выполнены.

При N = 1 из определения де-юреправил модели следует, что:

- либо существует субъект s Î S ₀такой, что справедливо условие (s, y, a) Î E ₀и op ₁= grant (a, s, x, y);

- либо существует объект s Î O ₀такой, что справедливо условие (s, y, a) Î E ₀и op ₁= take (a, x, s, y)

Таким образом, для N = 1 условия теоремы выполняются.

Пусть N > 1, и утверждение теоремы истинно для k < N. Тогда (x, y, a) Ë E_{N – 1}и ребро (x, y, a) появляется в графе доступов G_N в результате применения к графу G_{N – 1} некоторого правила op_N. Возможны два случая: x Ï S ₀и x Î S ₀.

Если x Ï S ₀, то существует x ₁Î S_{N – 1}: op_N = grant (a, x ₁, x, y). Также возможны два случая: x ₁Î S ₀или x ₁Ï S ₀.

Если x ₁Î S ₀, тогда истинен предикат can_share ({ g }, x ₁, x, G ₀) с числом преобразований графов меньшим N. Следовательно, по предположению индукции существуют:

- x ₂Î O ₀: (x _2, x, g) Î E ₀;

- x ’Î S ₀, соединенный с x ₂конечным пролетом моста;

- острова I ₁, …, I_t, где t ³ 1, такие, что x ₁Î I_t, x ’Î I ₁, и существуют мосты между островами I_j и I_{j + 1} для j = 1, …, t – 1.

Кроме того, истинен предикат can_share (a, x ₁, y, G ₀) с числом преобразований графов меньшим N. Тогда по предположению индукции существуют:

- s Î O ₀: (s_, y, a) Ì E ₀;

- s ’Î S ₀: s = s ’или s ’соединен с s конечным пролетом моста;

- острова I_t, …, I_u, где t – u ³ 1, такие, что x ₁Î I_t, s ’Î I_u, и существуют мосты между островами I_j и I_{j + 1} для j = t, …, u – 1.

Дата добавления: 2014-11-20