Расширенная модель Take-Grant 1 страница

1. Направления развития модели Take-Grant

Рассмотренные в классической модели Take-Grant способы анализа путей распространения прав доступа в системах с дискреционным управлением доступом имеют в большей степени теоретическое значение, так как, как правило, в реальных КС не реализуются столь сложные графы доступов, для анализа которых необходимо использовать теоремы 5.1-5.3. В то же время на основе классической модели были разработаны ее расширения, которые развивают идеи классической модели, предлагая новые механизмы анализа, в большей степени применимые к современным системам защиты информации.

Рассмотрим три расширения модели.

1. Де-факто правила, предназначенные для поиска и анализа информационных потоков.

2. Алгоритм построения замыкания графа доступов и информационных потоков.

3. Способы анализа путей распространения прав доступа или информационных потоков.

2. Де-факто правила расширенной модели Take-Grant

Вместо прав доступа take и grant в расширенной модели в первую очередь рассматриваются права доступа read и write, наличие которых у субъектов системы является причиной возникновения информационных потоков.

Расширенная модель Take-Grant строится на основе классической модели. Ее основными элементами являются:

O ¾ множество объектов;

S Í O ¾ множество субъектов;

R = { r ₁, r ₂, …, r_m } È { t, g } È { r, w } ¾ множество видов прав доступа и видов информационных потоков, где r (read) ¾ право на чтение или информационный поток на чтение, w (write) ¾ право на запись или информационный поток на запись;

G = (S, O, E È F) ¾ конечный помеченный ориентированный без петель граф доступов и информационных потоков, описывающий состояние системы. Элементы множеств S, O являются вершинами графа. Элементы множества E Í O ´ O ´ R являются «реальными» ребрами графа, соответствующими правам доступа, и в графе доступов обозначаются сплошными линиями. Элементы множества F Í O ´ O ´ { r, w }являются «мнимыми» ребрами, соответствующими информационным потокам, и в графе доступов обозначаются пунктирными линиями. Каждое «реальное» ребро помечено непустым подмножеством множества видов прав доступа R, каждое «мнимое» ребро помечено непустым подмножеством множества { r, w }.

Порядок перехода системы расширенной модели Take - Grant из состояния в состояние определяется де-юреи де-фактоправилами преобразования графа доступов и информационных потоков. Преобразование графа G в граф G ’в результате выполнения правила op обозначим следующим образом:

G ├ _op G ’.

Определение де-юре правил take, grant, create, remove совпадает с определением этих правил в классической модели Take-Grant. Де-юреправила применяются только к «реальным» ребрам (элементам множества E).

Де-факто правила применяются к «реальным» или «мнимым» ребрам (элементам множества E È F), помеченным r или w. Результатом применения де-фактоправил является добавление новых «мнимых» ребер во множество F. Рассматриваются шесть де-факто правил: два вспомогательных и четыре основных.

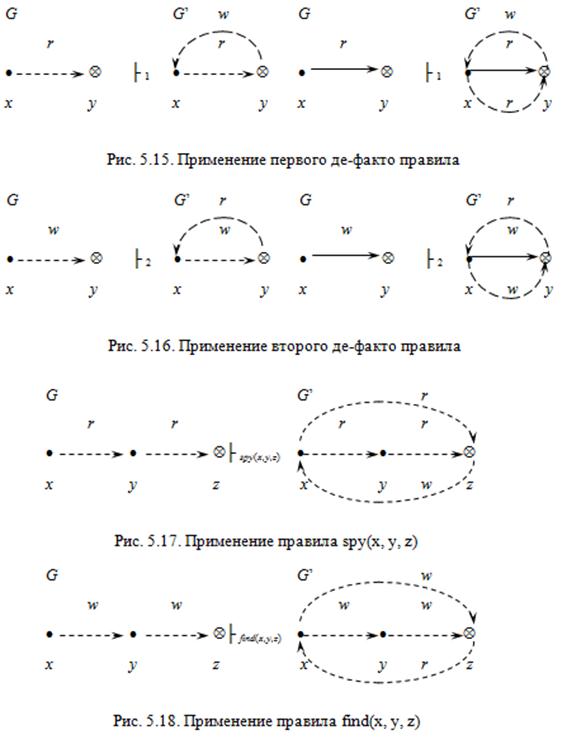
Рассмотрим порядок применения де-юре правил преобразования графа доступов. В отличие от де-юре правил, для применения трех из шести де-факто правил требуется участие двух субъектов (рис. 5.15-5.20).

Рассмотрим условия применения де-факто правил в исходном состоянии G = (S, O, E È F) и результаты их применения в результирующем состоянии G ’= (S, O, E È F ’) (табл. 5.2).

Таблица 5.2. Де-факто правила расширенной модели Take - Grant

Правила	Исходное состояние G = (S, O, E È F)	Результирующее состояние G ’= (S, O, E È F ’)
первое правило	x Î S, y Î O, (x, y, r) Î E È F	F ’= F È {(y, x, w), (x, y, r)}
второе правило	x Î S, y Î O, (x, y, w) Î E È F	F ’= F È {(y, x, r), (x, y, w)}
spy (x, y, z)	x, y Î S, x ¹ z, {(x, y, r), (y, z, r)} Ì E È F	F ’= F È {(x, z, r), (z, x, w)}
find (x, y, z)	x, y Î S, z Î O, x ¹ z, {(x, y, w), (y, z, w)} Ì E È F	F ’= F È {(x, z, w), (z, x, r)}
post (x, y, z)	x, y Î S, z Î O, x ¹ y, {(x, z, r), (y, z, w)} Ì E È F	F ’= F È {(x, y, r), (y, x, w)}
pass (x, y, z)	x Î S, y, z Î O, y ¹ z {(x, y, w), (x, z, r)} Ì E È F	F ’= F È {(y, z, r), (z, y, w)}

Из определения де-фактоправил следует, что для анализа информационных потоков достаточно рассматривать потоки одного вида либо на чтение, либо на запись. В дальнейшем будем рассматривать только информационные потоки на запись. Будем также предполагать, что при возникновении информационного потока не накладывается ограничений на кооперацию субъектов системы, участвующих в этом процессе.

Определение 5.8. Пусть x, y Î O ₀, x ¹ y ¾ различные объекты графа доступов и информационных потоков G ₀= (S ₀, O ₀, E ₀È F ₀). Определим предикат can_write (x, y, G ₀), который будет истинным тогда и только тогда, когда существуют графы G ₁= (S ₁, O _1, E ₁ È F ₁), …, G_N = (S_N, O_N, E_N È F_N) и де-юре или де-факто правила op ₁, …, op_N такие, что G ₀├ _{op 1} G ₁├ _{op 2}… ├ _opN G_N и (x, y, w) Î F_N, где N ³ 0.

Для проверки истинности предиката can_write (x, y, G ₀), также следует определить необходимые и достаточные условия, задача проверки которых алгоритмически разрешима.

Теорема 5.4. Пусть G ₀= (S ₀, O ₀, E ₀È F ₀) граф доступов и информационных потоков, x, y Î O ₀, x ¹ y. Тогда предикат can_write (x, y, G ₀) истинен тогда и только тогда, когда существуют объекты o ₁, …, o_m Î O ₀, где o ₁= x, o_m = y, такие, что или m = 2 и (x, y, w) Î F ₀, или для i = 1, …, m – 1 выполняется одно из условий:

- o_i Î S ₀и или истинен предикат can_share ({ w }, o_i, o_{i +1}, G ₀), или (o_i, o_{i + 1}, w) Î E ₀È F ₀;

- o_{i + 1} Î S ₀и или истинен предикат can_share ({ r }, o_{i + 1}, o_i, G ₀), или (o_{i + 1}, o_i, r) Î E ₀È F ₀;

- o_i, o_{i + 1} Î S ₀и или истинен предикат can_share (a, o_i, o_{i + 1}, G ₀), или истинен предикат can_share (a, o_{i + 1}, o_i, G ₀), где a Î { t, g }.

Доказательство. Доказательство теоремы осуществляется аналогично доказательству теорем 1.5 и 1.6. ■

2. Построение замыкания графа доступов и информационных потоков

Для проверки истинности предиката can_share (a, x, y, G ₀) или can_write (x, y, G ₀) для многих пар вершин неэффективно использовать алгоритмы проверки условий теорем 1.5, 1.6, 1.8. Эффективнее применять алгоритмы, позволяющие осуществить проверку истинности данных предикатов сразу для всех пар вершин. Такие алгоритмы реализуют преобразование графа доступов и информационных потоков в его замыкание.

Определение 5.91. Пусть G = (S, O, E È F) ¾ граф доступов и информационных потоков такой, что для каждого s Î S существует o Î O и при этом (s, o, { t, g, r, w }) Ì E. Тогда замыканием (или де-факто-замыканием) графа G называется граф доступов и информационных потоков G * = (S, O, E* È F*), полученный из G применением последовательности правил take, grant и де-факто правил. При этом применение к графу G* указанных правил не приводит к появлению в нем новых ребер.

Алгоритм построения замыкания графа доступов состоит из трех этапов:

1. Построение tg -замыкания.

2. Построение де-юре-замыкания.

3. Построение замыкания.

Определение 5.10. Пусть G = (S, O, E È F) ¾ граф доступов и информационных потоков такой, что для каждого s Î S существует o Î O и при этом (s, o, { t, g, r, w }) Ì E. Тогда tg -замыканием графа G называется граф доступов и информационных потоков G^tg = (S, O, E^tg È F), полученный из G применением последовательности правил take или grant. При этом каждое ребро (o ₁, o ₂, a) Î E^tg \ E имеет вид (o ₁, o ₂, t) или (o ₁, o ₂, g), и применение к графу G^tg правил take или grant не приводит к появлению в нем новых ребер указанного вида.

Определение 5.11. Пусть G = (S, O, E È F) ¾ граф доступов и информационных потоков такой, что для каждого s Î S существует o Î O и при этом (s, o, { t, g, r, w }) Ì E. Тогда де-юре-замыканием графа G называется граф доступов и информационных потоков G ^де-юре = (S, O, E ^де-юреÈ F), полученный из G применением последовательности правил take или grant. При этом применение к графу G ^де-юреправил take или grant не приводит к появлению в нем новых ребер.

Алгоритм 5.1. Алгоритм построения tg -замыкания графа доступов и информационных потоков G = (S, O, E È F) состоит из пяти шагов.

Шаг 1. Для каждого s Î S выполнить правило create ({ t, g, r, w }, s, o); при этом создаваемые объекты занести во множество O, создаваемые ребра занести во множество E.

Шаг 2. Инициализировать: L­ = {(x, y, a) Î E: a Î { t, g }} ¾ список ребер графа доступов и информационных потоков и N = Æ ¾ множество вершин.

Шаг 3. Выбрать из списка L первое ребро (x, y, a). Занести x, y во множество N. Удалить ребро (x, y, a) из списка L.

Шаг 4. Для всех вершин z Î N проверить возможность применения правил take или grant на тройке вершин x, y, z с использованием ребра (x, y, a), выбранном на шаге 3. Если в результате применения правил take или grant появляются новые ребра вида (a, b, b), где { a, b } Ì { x, y, z } и b Î { t, g }, занести их в конец списка L и множество E.

Шаг 5. Пока список L не пуст, перейти на шаг 3.

Очевидно, что вычислительная сложность данного алгоритма пропорциональна | O |³.

Теорема 5.4. Алгоритм 5.1 корректно строит tg -замыкание графа доступов и информационных потоков.

Доказательство. Пусть G ’= (S, O, E ’È F) ¾ граф доступов и информационных потоков, полученный из G = (S, O, E È F) после применения алгоритма 1.3. Пусть G^tg = (S, O, E^tg È F) ¾ tg -замыкание графа G. Необходимо доказать, что G ’= G^tg.

Техника доказательства теоремы аналогична технике доказательства леммы 1.3.

Докажем от противного. Пусть существует ребро (x, y, a) Î E^tg \ E ’, где a Î { t, g }. Тогда существуют два ребра (a, b, b), (c, d, g) Î E^tg, использованные в правиле take или grant, применение которого привело к появлению ребра (x, y, a), где { x, y } Ì { a, b, c, d }, |{ a, b, c, d }| = 3, b, g Î { t, g }.

Если (a, b, b), (c, d, g) Î E ’, то согласно описанию алгоритма 1 ребро (x, y, a) Î E ’¾ противоречие. Следовательно, или (a, b, b) Î E^tg \ E ’, или (c, d, g) Î E^tg \ E ’. В то же время граф G^tg получен из G в результате применения конечной последовательности правил take и grant. Ребра (a, b, b), (c, d, g) должны быть получены раньше, чем ребро (x, y, a). Таким образом, повторяя рассуждения для ребер, с использованием которых получены ребра (a, b, b), (c, d, g), придем к противоречию, так как все ребра графа G изначально содержатся в графе G ’. Следовательно, E^tg = E ’и G ’= G^tg.

Теорема доказана. ■

Алгоритм 5.2. Алгоритм построения де-юре-замыкания графа доступов и информационных потоков G = (S, O, E È F) состоит из четырех шагов.

Шаг 1. Выполнить алгоритм 1.3.

Шаг 2. Для каждой пары ребер вида (x, y, t), (y, z, a) Î E^tg, где x Î S, применить правило take (a, x, y, z) и, если полученное ребро (x, z, a) Ï E^tg, то занести его во множество E^tg.

Шаг 3. Для каждой пары ребер вида (x, y, g), (x, z, a) Î E^tg, где x Î S, применить правило grant (a, x, y, z) и, если полученное ребро (у, z, a) Ï E^tg, то занести его во множество E^tg.

Шаг 4. Для каждой пары ребер вида (x, y, t), (y, z, a) Î E^tg, где x Î S, применить правило take (a, x, y, z) и, если полученное ребро (x, z, a) Ï E^tg, то занести его во множество E^tg.

Теорема 5.5. Алгоритм 5.2 корректно строит де-юре замыкание графа доступов и информационных потоков.

Доказательство. После построения tg- замыкания на первом шаге алгоритма 1.4 всем субъектам графа доступов необходимо выполнить две последовательности действий:

- используя правило grant, раздать права доступа, и, используя правило take, забрать права доступа (рис. 5.21(а));

- используя правило take, забрать права доступа, и, используя правило grant, раздать права доступа (рис. 5.21(б)).

Объединяя указанные последовательности, получаем шаги 2-4 алгоритма. Теорема доказана. ■

Алгоритм 5.3. Алгоритм построения де-факто - замыкания графа доступов и информационных потоков G = (S, O, E È F) состоит из шести шагов:

Шаг 1. Выполнить алгоритм 1.4.

Шаг 2. Для всех ребер (x, y, a) Î E ^де-юреÈ F, где x Î S, a Î { w, r }, применить первые два де-факто правила. Если будут получены новые ребра, то занести их во множество F.

Шаг 3. Инициализировать: L­ = {(x, y, a) Î E ^де-юреÈ F: a Î { w, r }} ¾ список ребер графа доступов и информационных потоков и N = Æ ¾ множество вершин.

Шаг 4. Выбрать из списка L первое ребро (x, y, a). Занести x, y во множество N. Удалить ребро (x, y, a) из списка L.

Шаг 5. Для всех вершин z Î N проверить возможность применения де-фактоправил на тройке вершин x, y, z с использованием ребра (x, y, a). Если в результате применения де-фактоправил spy, find, post, pass появляются новые ребра вида (a, b, b), где { a, b } Ì { x, y, z } и b Î { r, w }, то занести их в конец списка L и множество F.

Шаг 6. Пока список L не пуст, перейти на шаг 4.

Теорема 5.5. Алгоритм 5.3 корректно строит де-факто-замыкание графа доступов и информационных потоков.

Доказательство. Алгоритм 5.3 аналогичен алгоритму 5.1. Следовательно, доказательство теоремы 5.5 аналогично доказательству теоремы 5.3. ■

3. Анализ путей передачи прав доступа и создания информационных потоков

Рассмотрим задачу поиска и анализа информационных потоков в ином свете. Допустим, факт нежелательной передачи прав или информации уже состоялся. Каков наиболее вероятный путь его осуществления? В классической модели Take-Grant не дается прямого ответа на этот вопрос. Можно говорить, что есть возможность передачи прав доступа или возникновения информационного потока, но нельзя определить, какой из путей при этом использовался.

Рассмотрим подходы к решению задачи определения возможных путей передачи прав доступа или возникновения информационных потоков.

Предположим, что чем больше узлов на пути между вершинами, по которому произошла передача прав доступа или возник информационный поток, тем меньше вероятность использования этого пути.

Рассмотрим пример, представленный на рис. 5.22.

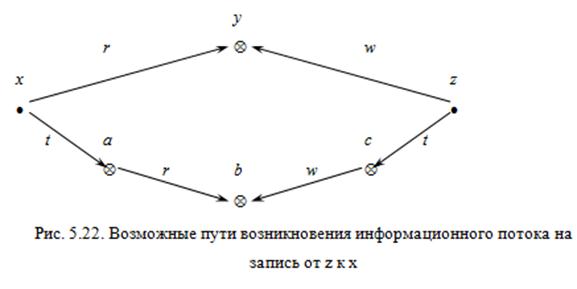
Интуитивно ясно, что наиболее вероятный путь передачи информации от субъекта z к субъекту x лежит через объект y. В то же время нарушитель для большей скрытности может специально использовать более длинный путь через a, b, c. Особенно, если предположить, что информация в объекте y контролируется администратором безопасности системы.

Рассмотрим другой пример. Какой из двух путей возникновения информационного потока, представленных рис. 5.23, более вероятный?

Путь, представленный на рис. 5.23(в) реализуется за счет активных действий субъекта x, заинтересованного в возникновении информационного потока. По этой причине наиболее вероятным, как правило, будет именно этот путь.

Таким образом, в расширенную модель Take-Grant можно включить понятие вероятности или стоимости пути передачи прав доступа или информации. Путям меньшей стоимости соответствует наивысшая вероятность, и их надо исследовать в первую очередь. Есть два основных подхода к определению стоимости путей.

Первый подход основан на присваивании стоимости ребрам графа доступов, находящимся на пути передачи прав доступа или возникновения информационного потока. В этом случае стоимость ребра определяется в зависимости от прав доступа, которыми оно помечено, а стоимость пути есть сумма стоимостей пройденных ребер.

Второй подход основан на присваивании стоимости каждому используемому де-юреили де-факто правилу. Стоимость правила при этом может быть выбрана, исходя из условий функционирования системы Take-Grant и может:

· являться константой;

· зависеть от специфики правила;

· зависеть от числа и состава участников при применении правила;

· зависеть от степени требуемого взаимодействия субъектов.

Стоимость пути в этом случае определяется как сумма стоимостей примененных правил.

Представление систем Take-Grant системами ХРУ

Решение задачи представления систем классической модели Take-Grant системами модели ХРУ позволяет лучше изучить основные свойства двух моделей систем дискреционного управления доступом.

Построим гомоморфизм системы Take-Grant и системы ХРУ.

Пусть состояние системы Take-Grant описывается графом G = (S_tg, O_tg, E), а R_tg ¾ множество прав доступа системы Take-Grant.

Положим для системы ХРУ:

R­ ­= R_tg È { own } ¾ множество прав доступа;

S ­ = O = O_tg ¾ множество субъектов и объектов системы ХРУ;

M _{| S | ´ | S |} ¾ матрица доступов, где для x, y Î O_tg, если (x, y, r) Î E, то r Î M [ x, y ], и для s Î S_tg выполняется условие own Î M [ s, s ];

q = (S, O, M) ¾ состояние системы.

Переход системы ХРУ в соответствии с правилами модели Take-Grant осуществляется в результате применения команд пяти видов для каждого a = { r ₁, …, r_k } Ì R_tg.

1. command take _a(x, y, z)

if (own Î M [ x, x ]) and (t Î M [ x, y ]) and (r ₁Î M [ y, z ]) and …

and (r_k Î M [ y, z ]) then

«внести» право r ₁в M [ x, z ];

…

«внести» право r_k в M [ x, z ];

endif

end.

2. command grant _a(x, y, z)

if (own Î M [ x, x ]) and (g Î M [ x, y ]) and (r ₁ Î M [ x, z ]) and …

and (r_k Î M [ x, z ]) then

«внести» право r ₁в M [ y, z ];

…

«внести» право r_k в M [ y, z ];

endif

end.

3. command create _ object_ a(x, y)

if (own Î M [ x, x ]) then

«создать» субъекта у;

«внести» право r ₁в M [ x, y ];

…

«внести» право r_k в M [ x, y ];

endif

end.

4. command create _ subject_ a(x, y)

if (own Î M [ x, x ]) then

«создать» субъекта у;

«внести» право own в M [ y, y ];

«внести» право r ₁в M [ x, y ];

…

«внести» право r_k в M [ x, y ];

endif

end.

5. command remove_ a(x, y)

if (own Î M [ x, x ]) then

«удалить» право r ₁из M [ x, y ];

…

«удалить» право r_k из M [ x, y ];

endif

end.

В приведенных командах, реализующих правила take и grant, не учитывается случай, когда выполняется условие x = z. В модели Take-Grant не допускается появление петель в графе доступов. Таким образом, в командах take _a(x, y, z) и grant _a(x, y, z) системы ХРУ следует осуществить проверку условия x ¹ z. Непосредственная реализация проверки данного условия потребует значительного усложнения рассмотренного представления систем Take-Grant системами ХРУ и выходит за рамки рассматриваемых в пособии вопросов моделирования управления доступом и информационными потоками в КС.

Кроме того, если исключить из определения модели Take-Grant требование отсутствия петель в графе доступов, то рассмотренные в модели условия передачи прав доступа и реализации информационных потоков существенно не изменятся.

Контрольные вопросы

1. Выразите команду spy расширенной модели Take-Grant через ее другие де-факто команды.

2. Как по аналогии с определением безопасного начального состояния в модели ХРУ и с использованием определения предиката can_share(a, x, y, G₀) определить безопасное начальное состояние в модели Take-Grant?

Дата добавления: 2014-11-20