
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення. Нехай . Розглянемо образ інтервалу при відображенні
|
|
|
|
Доведення.
Нехай 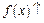 . Розглянемо образ інтервалу
. Розглянемо образ інтервалу  при відображенні
при відображенні  . Множина
. Множина  обмежена зверху,
обмежена зверху, 
 , а значить має точну верхню межу. Позначимо її
, а значить має точну верхню межу. Позначимо її  .
.
Доведемо, що  . Візьмемо довільне
. Візьмемо довільне 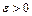 . Число
. Число  не є верхньою межею
не є верхньою межею 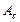 , це означає, що
, це означає, що 
 . Візьмемо
. Візьмемо  , тоді
, тоді  :
: 
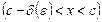
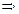
 . Значить,
. Значить,  .
.
Таким чином, для 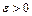 ми вказали
ми вказали 

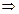
 , тобто за означенням Коші
, тобто за означенням Коші  .
.
Аналогічно доводиться існування  .
.
Зауваження. Якщо функція визначена і монотонна на відрізку 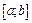 , то вона має в точці
, то вона має в точці 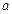 правосторонню границю, а в точці
правосторонню границю, а в точці 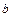 лівосторонню.
лівосторонню.
Будемо говорити, що функція  неперервна на відрізку
неперервна на відрізку 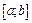 , якщо вона неперервна на
, якщо вона неперервна на 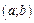 а також в точці
а також в точці 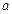 неперервна справа, а в точці
неперервна справа, а в точці 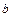 – зліва.
– зліва.
Теорема 2. Нехай 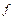 - монотонна функція на відрізку
- монотонна функція на відрізку 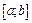 , значення якої заповнюють відрізок, тоді
, значення якої заповнюють відрізок, тоді 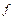 неперервна на
неперервна на 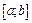 .
.
Розглянемо внутрішню точку  і доведемо, що
і доведемо, що 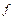 в точці
в точці 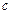 неперервна.
неперервна.
Для визначеності нехай 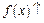 . Очевидно,
. Очевидно, 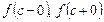 існують і
існують і  . Припустимо, що
. Припустимо, що 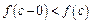 . Тоді для
. Тоді для 
 :
:  (точка
(точка 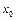 існує, оскільки значення функції заповнюють відрізок). Очевидно,
існує, оскільки значення функції заповнюють відрізок). Очевидно, 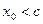 в силу монотонності функції, і
в силу монотонності функції, і 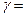
 оскільки
оскільки  .
.
Одержали суперечність, оскільки  . Отже, припущення
. Отже, припущення 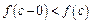 неправильне, і
неправильне, і  .
.
Аналогічно одержимо  .
.
Таким чином,  , тобто
, тобто 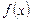 неперервна в точці
неперервна в точці 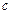 .
.
Аналогічно доводиться неперервність функції в точці 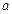 справа і в точці
справа і в точці 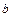 зліва.
зліва.
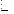
4.8. Неперервність елементарних функцій
1. Будь-який многочлен є неперервним на всій числовій прямій.
Якщо  , то
, то  неперервна. Справді, для
неперервна. Справді, для 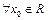




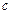
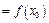 .
.
Функція  неперервна на числовій прямій. Дійсно, для
неперервна на числовій прямій. Дійсно, для 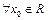
 .
.  , якщо
, якщо 
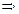

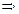
 - неперервна.
- неперервна.
Функція 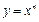 - неперервна, як добуток
- неперервна, як добуток 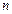 неперервних функцій
неперервних функцій  .
.
Многочлен  - одержано з функцій
- одержано з функцій  і
і  за допомогою арифметичних операцій, отже, він є неперервним на всій числовій прямій.
за допомогою арифметичних операцій, отже, він є неперервним на всій числовій прямій.
2. Дробово-раціональна функція 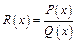 , де
, де  - неперервні многочлени, є неперервною для
- неперервні многочлени, є неперервною для  :
: 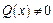 .
.
|
|
|
3. Ірраціональні і дробово-ірраціональні функції неперервні. 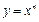 - неперервна при
- неперервна при 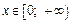 і
і  , тоді
, тоді 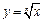 неперервна на
неперервна на  .
.
 - неперервна, як суперпозиція неперервних функцій.
- неперервна, як суперпозиція неперервних функцій.
4. Тригонометричні і обернені тригонометричні функції неперервні.
 .
.

 ,
, 
 .
.

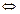

 .
.
З останньої нерівності випливає, що  (справедливо для
(справедливо для  ).
).
Далі, нехай 

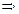
 і
і 
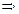

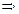
 - неперервна на
- неперервна на  .
.

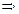
 - неперервна на
- неперервна на 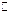 .
.
 и
и  неперервні на своїх областях визначення.
неперервні на своїх областях визначення.
 ,
,  ,
,  ,
,  - неперервні за наслідком як обернені функції до неперервних.
- неперервні за наслідком як обернені функції до неперервних.
5.  - неперервна. Доведемо, що
- неперервна. Доведемо, що  . Нехай
. Нехай 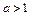 , тоді
, тоді  ,
,  ,
, 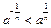 . Для
. Для 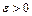
 :
:  виконується
виконується  ,
,  , отже,
, отже,  . Для
. Для  :
:  виконується
виконується 
 , отже
, отже  ,
,  , тобто
, тобто  .
.
Нехай  ,
,  . Отже,
. Отже,  . Це означає, що
. Це означає, що  , отже,
, отже,  - неперервна.
- неперервна.
6.  - неперервна, як обернена до
- неперервна, як обернена до  (неперервної і монотонної).
(неперервної і монотонної).
Теорема. Будь-яка елементарна функція неперервна в своїй області визначення.
4.9. Важливі границі
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
Доведемо першу важливу границю  .
.
Відомо, що  при
при  .
.
Тоді 
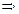

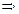
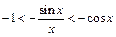
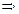
 і, оскільки,
і, оскільки,
 , то
, то  .
.
Звідси при  за теоремою про двох міліціонерів одержимо:
за теоремою про двох міліціонерів одержимо:
 .
.
Отже,  .
. 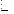
Наслідки.
1) 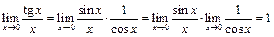 ;
;
2)  ;
;
3)  .
.
Доведемо другу важливу границю  .
.
Нехай 
 ,
,  . Тоді
. Тоді 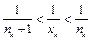 .
.

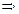

 .
.
За означенням границі за Гейне  .
.
Нехай  . Позначимо
. Позначимо  .
.
Тоді





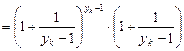
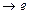 .
.
За означенням границі за Гейне  .
.
Таким чином  або
або 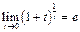 .
. 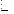
Доведемо  .
.
Дійсно,  . Зважаючи на неперервність функції
. Зважаючи на неперервність функції  і
і  одержимо
одержимо  .
. 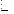
Доведемо  .
.
Нехай 
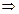

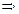
 , значить,
, значить, 
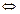
 .
.
Отже,  .
. 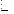
Доведемо  .
.
Нехай 
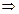

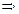
 .
. 
 .
.
Отже,

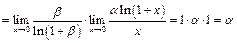 .
. 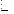
4.10. Порівняння функцій. Еквівалентні функції
Означення. Ф ункції 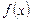 і
і 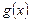 називаються еквівалентними при
називаються еквівалентними при  , якщо
, якщо  . При цьому пишуть
. При цьому пишуть 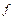 ~
~ 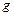 ,
,  .
.
Теорема. Нехай  ~
~  ,
,  і
і 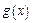 ~
~  ,
,  , тоді:
, тоді:
1)  ;
;
2) 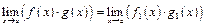
при умові, що границі, які розглядаються, існують (скінченні чи нескінченні).
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 445; Нарушение авторских прав?; Мы поможем в написании вашей работы!