Примеры выполнения заданий

0)

9)

8)

7)

6)

5)

4)

3)

2)

1)

9)

8)

7)

6)

5)

4)

3)

2)

1)

0)

Примеры выполнения заданий

1. Приведите формулу логики предикатов к приведенной форме: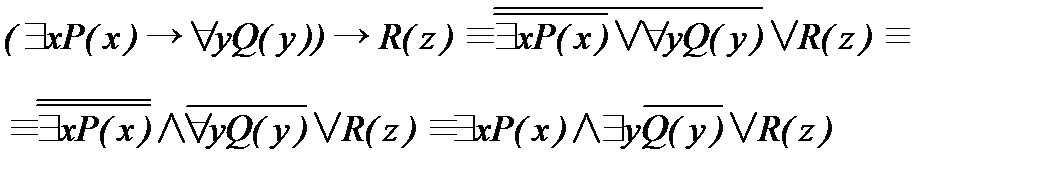

2. Приведите формулу логики предикатов к приведенной форме, где x, y, z – вещественные переменные, применив отрицание к формуле:

"y $x ((y ¹ x) Ú Ø"y (x < y) & "z (y - x £ z)).

Ø ("y $x ((y ¹x)Ú Ø"y (x < y) & "z (y - x £ z))) º

º $y "x ((y = x) & "y (x < y) Ú $z (y - x ≥ z))

3. Приведите формулу логики предикатов к предваренной нормальной форме $x"yP(x, y) Ú Ø"x$yQ(x, y).

$x"yP(x, y) Ú Ø"x$yQ(x, y)º $x"yP(x,y) Ú $x"yØQ(x, y) º

º $x("yP(x, y) Ú "yØQ(x, y)) º $x("yP(x, y) Ú "аØQ(x,а)) º

º $x"y"а (P(x, y) Ú "аØQ(x, а)).

Задания для самостоятельного выполнения

1.Приведите формулу логики предикатов к приведенной нормальной форме:

Ø"y $x T(y, x) Ú $y"x Q(y, x);

$x (Ø"y U(y, x) & $z$y L(y, z, x));

"x Ø("y A(x, y) ®$y H(z, x));

Ø"y"z U(y, z) ~ "x $y Q(y, x);

"y Ø($x G(y, x) ® "z $x N(y, x, z));

$x "y (Ø(E(y, x) & $z Q(y, z)));

$t (Ø("y K(y, t) ~ $y $z Q(y, t, z)));

"z"x A(x, z) Ú "y"z Q(y, x);

$y"x M(y, x) & $y"z Q(y, z);

$t Ø("y K(y, t) ®$x $y F(y, x, t));

"z"y Ø($x G(z, y) ~ "x"s N(x, s));

Ø"s$x U(s, x) Ú $y"x Q(y, x);

"y ("m U(y, m) & "x Q(y, x));

"x Ø($y A(x, y) ® (Ø$z"y D(y, z));

$x Ø($y"z P(z, x, y) Ú $z"y K(y, x, z));

$x"y T(y, x) ~ Ø$y"x P(y, x);

"y $z T(y, z) ~ "x "y Q(y, x));

$t Ø ("y U(y, t) Ú $y "x R(y, x));

"x (Ø($y G (y, x) ® Ø"y P(y, x));

"t (Ø$x "y N(y, x) & $y L(y, t));

"y ($x $z F(z, y, x) ® Ø"x Q(y, x));

$x "y (Ø "t U(t, y, x)) Ú Ø"x $y R(y, x);

"z Ø("y A(z, y) & Ø$x $y H(y, x));

$a $y U(y, a) ~ $t $a Q (a, t));

"y Ø($n A(n, y) ® $y "n H(y, n));

Ø"y"m U(y, m) Ú Ø"y"x D(y, x);

"x ($n C(n, x) ~ "t $y Q(y, x, t));

"n"m Ø"y G(n, y, m) & Ø"x$y B(y, x));

"z Ø("y C(z, y) ® $y $t "x Q(t, y, x));

$z "y U(z, y) & $x $z"m F(m, x, z);

"x Ø($y $t A(x, y, t) ~ "y $z Q(y, z));

"y"m U(y, m) Ú Ø"x$y $m K(m, x, y);

"z Ø($x A(x, z) ® $y Ø$z Q(y, z));

"y ("m U(y, m) & Ø$m"x F(y, x, m));

"x Ø("y$z K(x, z, y) ~ $y Q(y, x));

"x Ø("y"t U(t, y, x) Ú Ø$y$t R(y, t));

"t Ø($y $z H(t, y, z) ® $x "y G(y, x));

$x Ø"y U(y, x) & $x $y"z Q(y, z, x);

"y"x $z A(y, x, z) Ú "x$z B(z, x);

$x Ø("y K(y, x) ~ $y$z L(y, x, z)));

2. Приведите формулы логики предикатов к приведенной нормальной форме, где x, y, z – вещественные переменны, применив отрицание к формуле:

0)

"y ($x (y > x) Ú "t (y = t));

$x (Ø"y (y < x) É $z "t (z + x + y ³ t));

"x $y $z ((x + y > z) & (x + z > y) & (y + z > x));

"x "y (Ø"t (y ¹ t) É (y > x));

"y ($ x (y £ x) É "z ((y = x) Ú (y = z)));

$x "y (Ø(y – x > 0) & $z (y - z > 0));

$x "z (Ø($y (z ¹ y) Ú (z ¹x))) É (x + z < 0));

"t $x "y ((y < x) & (t > x));

"y $x ((y ¹x) & "z (y + x >z));

$t (Ø ("y (y = t)) É $x (t > x) Ú (y > t));

"x $z "y ((y – x >0) É "t (y – x > t));

$x "y (Ø (y > x) & $z (y < z));

"t (Ø($x (x = t)) É $y (y + t > x));

"y "z ((y > 0) Ú (z > y) & "x (y >x));

$x (Ø ("y (y = x)) É $z (y > z));

"z ($ y (z > 0) Ú "t (y < t));

"y $ x ((y – x > 0) Ú "z (y – z > x));

$x "y ((y = x) & $z ((z < x) Ú (z < y)));

"t $x ((t ¹ x) & "y (y ¹x) É (t ¹ x));

"z (Ø ("y ((z > y) & (y > 0))) É $x (y > x));

"y $x "z ((y + x +z ¹ 0) É "t ((t > y) Ú (t > x) Ú (t >z)));

"x ("z ((z² > x) & (x² > z)) Ú (Ø($y (y² > x))));

$y "z (Ø(z = y) É (y ¹ z));

"y ($t (y > t) & $x (y > x));

$y ($z (z = y) É (Ø($x (z = x))));

"x "y "z ((x + y > z) & (y + z > x) &(z + x > y));

"t (Ø($y ((t < 0) Ú (y < 0))) É (y + t > 0));

$z "y "x ((z – x > 0) Ú (y – x > 0));

"x (Ø("y (x > y)) É $z (x + z > y));

"y ($t (y ¹ t) & $x (y ¹ x));

$z "y ((z < 0) Ú (y < 0) Ú $x (x > y + z));

$x $z $ y (Ø((x > y) & (y > z)) É (x < z));

"x (Ø($ y (x + y > 0)) É $t (t – y + x >0));

"y "z ((y ¹ z) & "x (y ¹ x));

"x "y (Ø("z (y £ x)) & (y ³ z));

$z "x $t ((x + z > t) É $y (Ø(x + t + z < y)));

"z ($ y (z > y) É $x (x > z));

"x "z (Ø("y (y – x > 0)) & $t (y + z + t < 0));

$t "y ((y ¹ t) Ú "z (y - z ¹ t));

$x $t ("y (y > x) É $z(Ø(y + x + t > z)));

3. Приведите к предваренной нормальной форме следующие формулы логики предикатов:

"y $x T(y, x) Ú "z "x Q(z, x);

Ø"y "x U(y, x) & $x "y R(y, x);

"y $x T(y, x) É "y "x Q(y, x);

Ø"y "x U(y, x) É $x "y R(y, x);

"y "x $z K(y, x, z) É "x $z $y P(y, x, z);

1)

"y ($x "y G(y, x) Ú "s $x N(y, x, s));

"y Ø$x U(y, x) & "x "y Q(y, x);

$y "x $z H(x, y, z) É $y $x G(y, x);

"x Ø"y P(y, x) É $y $x Q(y, x);

$y "x $z U(x, y, z) É $y $x $z G(y, x, z);

2)

"y $x A(y, x) & $y "z P(y, z);

Ø"y $x K(y, x) Ú $z $y "x Q(y, x, z);

"x $y A(x, y) É $y Ø "x R(y, x);

"y "x U(y, x) É "x $y P(y, x);

"y $m $z P(y, m, z) É $m $y $z G(m, y, z);

3)

"x (Ø($y A(x, y) Ú $y P(y, x)));

$y "m U(y, m) & "x "y Q(y, x);

"z $x T(z, x) É "y $x U(y, x);

"x (Ø"y U(y, x) É $y Q(y, x));

"z $x "y Q(z, x, y) É "y $x A(y, x);

4)

$x "y T(y, x) Ú "y "x H(y, x);

"y Ø $x U(y, x) & $y "z Q(y, z);

"x Ø"y A(x, y) É $y "z T(y, z);

"y $m $z U(y, m, z) É $y $z Q(y, z);

$n "y "x P(n, y, x) É "y Ø"n "x R(n, y, x);

5)

$n "y "x P(n, y, x) & "y Ø$n A(n, y);

"y ("m U(y, m) Ú Ø"x "m Q (y, x, m));

$n "y "x P(n, y, x) É "y Ø$n A(n, y);

"y ("m $x U(y, x, m) É Ø"x "m Q (y, x, m));

"y Ø $x G(y, x) É "y "x Q(y, x);

6)

"z $x T(z, x) Ú "y $x U(y, x);

"x (Ø"y U(y, x) & "y Q(y, x));

$x "y T(y, x) É "y "x H(y, x);

"y Ø $x U(y, x) É $y "x Q(y, x);

"x $y R(x, y) É $y "x P(y, x);

7)

"x Ø"y A(x, y) Ú $y "z T(y, z);

"y $m $z U(y, m, z) & $x $y $z Q(y, x, z);

"x (Ø($y A(x, y) É $y P(y, x)));

$y "x U(y, x) É "x "y Q(y, x);

Ø"y $x P(y, x) É $z $y "x Q(y, x, z);

8)

"x $y A(x, y) Ú $y Ø $x R(y, x);

"y "z U(y, z) & "x $y P(y, x);

"y "z A(y, z) É $y "z P(y, z);

Ø"y $x K(y, x) É $z "y "x Q(y, x, z);

"y ($x $y T(y, x) É "s $x K(y, x));

9)

$y "x $z H(x, y, z) Ú $y "x G(y, x);

"x Ø"y P(y, x) & $y $x Q(y, x);

"y ($x $y G(y, x) É "s N(y, s));

"y Ø$x U(y, x) É $x "y Q(y, x);

"y Ø$x H(y, x) É "x "y P(y, x);

Практическое занятие №13. Применение логики
предикатов.

Язык логики предикатов удобен для записи математических предложений и определений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства.

Запишите определение на языке логики предикатов, используя ограниченные кванторы, и постройте его отрицание:

Функция f непрерывна в точке x₀, если и только если для всякого положительного числа e существует положительное число d такое, что для всякого x из области определения D функции f, если |x - x₀| < d, то |f(x) - f(x₀)| < e.

Решение. Запишем это определение на языке логики предикатов двумя разными способами.

1 способ:

, где

2 способ, используя ограниченные кванторы:

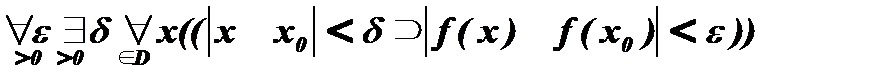
Построим отрицание этого определения:

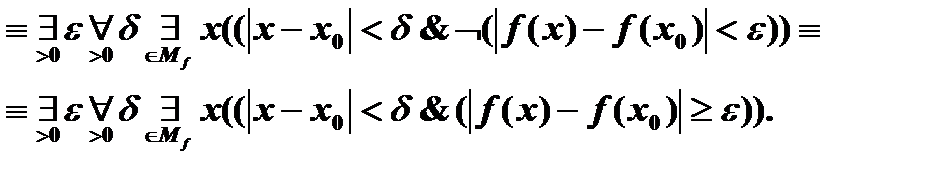
Задания для самостоятельного выполнения

1. Запишите аксиомы положительных величин на языке логики предикатов, используя ограниченные кванторы:

0) Коммутативность сложения

Для любых двух величин a, b Î A справедливо a + b = b + a.

1) Ассоциативность сложения

Для любых двух величин a, b, с Î A справедливо a + (b + c) = (a + b) + c.

2) Монотонность сложения

Для любых двух величин a, b Î A справедливо a + b > a.

3) Транзитивность отношения

Для любых трех величин a, b, с Î A. Если a < b и b < c, то a < c.

4) Возможность суммирования

Для любых двух величин a, b, с Î A существует однозначно определенная величина c = a + b.

5) Возможность вычитания

Для любых двух величин a, b, с Î A если a > b, то существует одна и только одна величина c Î A, для которой b + c = a.

6) Возможность деления

Какова бы ни была величина a Î A и натуральное число n, найдется такая величина b Î A, что n * b = a.

7) Возможность сравнения

Для любых двух величин a, b Î A имеет место одно из трех отношений:
a = b, a < b, a > b.

8) Аксиома Архимеда или Евдокса

Каковы бы ни были величины a, b Î A, существует такое n, что n* b > a

9) Аксиома соизмеримости отрезков

Пусть последовательность величин a_i Î A, i = 1…n обладает свойством
a₁ < a₂ <… < a_n <…, а последовательность b_i Î A, i = 1…n свойством
b₁ < b₂ <… < b_n <…, при этом a_i < b_i для любых i, j Î N.

Пусть для любого e > 0 существует такое N(e), что при всех n > N разность |a_n – b_n| < e. Тогда существует единственный элемент cÎ A, удовлетворяющий условиям a_i < с, с < bj для любых i, j Î N.

2. Запишите некоторые аксиомы действительных чисел на языке логики предикатов, используя ограниченные кванторы:

0) x + x’ = 0 (для любого x Î R существует x’Î R, противоположный x)

1) x ¹ y Þ x > y или y > x (для любых x, yÎ R)

2) (x * y) * z = x * (y * z) (для любых x, y, zÎ R)

3) Ø x > x (для любого xÎ R)

4) (x + y) * z = x * z + y * z (для любых x, y, zÎ R)

5) (x > y, y > z) Þ (x > z) (для любых x, y, zÎ R)

6) x ¹ 0 Þ x* x’ = 1 (для любого xÎ R. и x ¹ 0 существует x’Î R, x’ – обратный элемент для x)

7) (x > y) Þ (x + z > y +z) (для любых x, y, zÎ R)

8) x * 1 = x, 1Î R (для любого xÎ R)

9) (x > y, z > 0) Þ (x* z > y * z) (для любых x, y, zÎ R)

3. Подберите элементарные предикаты и запишите следующие высказывания:

0) a) каждое положительное действительное число является квадратом другого;

b) натуральное число, которое делится на 6, разделится и на 2;

1) a) для каждого натурального числа существует одно и только одно число, непосредственно следующее за ним;

b) каждое действительное число является кубом другого;

2) a) натуральное число, которое делится на 6, разделится и на 3;

b) произведение двух натуральных чисел, одно из которых четное, другое нечетное, есть число четное;

3) a) от перемены мест сомножителей произведение не меняется;

b) натуральное число, которое делится на 2 и 3, разделится на 6;

4) a) натуральное число, которое делится на 9, разделится на 3;

b) от перемены мест слагаемых сумма не меняется;

5) a) частное от деления двух натуральных четных чисел, если оно существует, есть число четное или нечетное;

b) если произведение двух натуральных чисел делится на 5, то хотя бы один из сомножителей делится на 5;

6) a) для чисел отличных от нуля существует наибольший общий делитель;

b) если произведение двух натуральных чисел делится на 12, то среди них есть четное число, делящееся на 3;

7) a) если произведение двух натуральных чисел делится на 18, то хотя бы один сомножитель делится на 6 или хотя бы один из сомножителей нечетный;

б) сумма двух натуральных чисел, имеющих различную четность, нечетна;

8) a) для чисел отличных от нуля существует наименьшее общее кратное;

б) если ни одно из двух натуральных чисел не делится на 11, то их произведение не делится на 11;

9) а) если произведение двух натуральных чисел делится на 12, то хотя бы один из сомножителей делится на 3 или хотя бы один из сомножителей четный;

б) сумма двух натуральных четных чисел, есть число четное.

4. Запишите определения на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:

0) Функция f (x) называется возрастающей в промежутке X из области определения, если для любых x1, x2Î X, из условия x1< x2 следует неравенство f(x1) < f(х2).

1) Прямая называется асимптотой графика функции y = f(x), если при удалении точки M в бесконечность по графику, расстояние от M до этой прямой стремится к нулю

2) Функция a(x) называется бесконечно малой при x®a, если для любого e>0 вблизи точки a выполняется неравенство |a(x)|<e (это значит, что существует проколотая окрестность точки a, в которой выполняется указанное неравенство)

3) Функция f непрерывна в точке a, если она определена в этой точке и разность f(x)-f(a) бесконечно мала при x®a, т.е. функция f непрерывна в точке a в том и только в том случае, когда .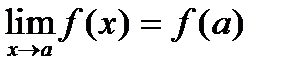

4) Функция f(x) бесконечно большая при x®a, если функция бесконечно мала при x®a.

5) Функция называется периодической, если существует такое число T, что для любого аргумента x число x± T принадлежит области определения и f(x ± T)=f(x).

6) Число А называется пределом бесконечной числовой последовательности {a_n} = a₁, a₂, a₃, …, a_i, …, a_n, …, если для всякого e>0 существует такое натуральное n_e, что для всякого номера n, если n> n_e, то |a_n - A|<e.

7) Функция f (x) называется убывающей в промежутке X из области определения, если для любых x1, x2Î X, из условия x1 < x2 следует неравенство f(x1) > f(х2).

8) Функция называется четной, если для любого аргумента x из области определения число -x также входит в область определения и f(-x)=f(x).

9) Функция f (x) называется убывающей в промежутке X из области определения, если для любых x1, x2Î X, из условия x1 < x2 следует неравенство f(x1) > f(х2).

5. Запишите определения на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:

0) Действительная функция f(x) действительного переменного x есть функция ограниченной вариации на интервале [a, b], если существует такое положительное число M, что для всех разбиений
a = x₀ < x₁ < … < x_n = b интервала [a, b] выполняется равенство

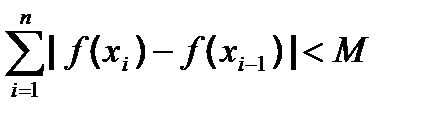
1) Абсолютным экстремумом числовой функции f называется точка P₀ в области определения D функции, обладающая свойством f(P₀) ³ f(P) для всех P, принадлежащих D (абсолютный максимум) или свойством f(P₀) £ f(P) для всех P, принадлежащих D (абсолютный минимум).

2) Однозначная функция f комплексного переменного z = x + iy называется аналитической функцией в точке z₀, если в некотором круге |z – z₀| < r с центром z₀ и радиусом r > 0 она определена и представима степенным рядом:

f(z) = a₀ + a₁(z - z₀) + … + a_n(z – z₀)ⁿ + …

3) Функция F(x) называется первообразной для функции f(x) на заданном промежутке (a, b) из ее области определения D(f), если для x из (a, b) выполняется равенство F’(x) = f(x).

4) Точка x₀ из области определения D(f) функции f называется точкой максимума этой функции, если найдется d - окрестность (x₀ - d;
x₀ + d) точки x₀, такая, что для всех x ¹ x₀ из этой окрестности выполняется неравенство f(x) £ f(x₀).

5) Число b называется пределом функции f(x), если для любого положительного числа e найдется такое положительное число d, что если всех x ® a, удовлетворяющих неравенству | x - a| < d, будет выполняться неравенство | f(x) - b| < e

6) Точка x₀ из области определения D(f) функции f называется точкой минимума этой функции, если найдется d - окрестность (x₀ - d; x₀ + d) точки x₀, такая, что для всех x ¹ x₀ из этой окрестности выполняется неравенство f(x) ³ f(x₀).

7) Вектор-функция v(t) ограничена, если для каждого положительного числа e существует такое число d, что из 0 < |t – t₁| < d следует |v(t) – v₁| < e

8) Аппроксимация функции f на отрезке [a, b] функциями X₁, X₂, …X_n, … при условии, что отклонение f от X_n измеряется с помощью
r(f, X_n) = max |f(X) - X_n(x)| при a £ x £ b, называется равномерной аппроксимацией.

9) Интервалом числовой прямой называется множество действительных чисел x, удовлетворяющих неравенству a < x < b, где a и b – действительные числа, x₀ = (a + b)/2- центр интервала. Интервал числовой прямой называется d - окрестностью точки x₀, если |x - x₀|< d.

6. Запишите теоремы и свойства на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:

0) Основная теорема алгебры.

Всякий отличный от константы многочлен вида:

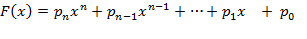
с действительными коэффициентами имеет, по крайней мере, один корень в поле комплексных чисел.

1) Общие свойства числовых полей:

Для любых элементов а и в поля F определены их сумма а + в и произведение а x в. В поле существует нуль и единица.

2) Основная теорема алгебры поЭйлеру:

Всякий многочлен с вещественными коэффициентами можно разложить в произведение линейных и квадратичных множителей с вещественными коэффициентами.

3) Теорема о достаточном условии монотонности

Если функция f(x) дифференцируема в промежутке X и f'(x)>0
(f'(x)<0) для всех xÎX, то f(x) возрастает (соответственно убывает) в промежутке X.

4) Следствие из основной теоремы алгебры:

Любой многочлен степени n над полем комплексных чисел имеет в нём ровно n корней, с учётом кратности корней.

5) Лемма Д'Аламбера

Если для какого-нибудь x f(x)≠0, где f(x) - многочлен степени ≥1, то найдется точка x₁ такая, что |f(x₁)|<|f(x)|.

6) Общие свойства числовых полей:

Для любого числового поля F справедливы тождества:

а + в = в + а (ав)с = а(вс)

(а + в)+ с = а+(в + с) а x 1= а

а + 0 = а а x 1/а = 1

а + (-а) = 0 а(в + с) = ав + ас

ав = ва

7) Теорема о производной

Функция y = f(x) имеет в точке x (конечную) производную в том и только в том случае, если она дифференцируема в этой точке. При этом верно равенство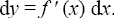

8) Общие свойства числовых полей:

Для любого числа а из поля F в F есть противоположное ему число –а, а если а ≠ 0, то и обратное ему число 1/а.

9) Теорема о достаточном условии выпуклости вверх и вниз

Если функция f(x) дифференцируема дважды в интервале X и в ней
f''(x) >0 (f''(x) <0), то f(x) является выпуклой вниз (соответственно выпуклой вверх) в интервале X.

7. Запишите теоремы на языке логики предикатов, используя ограниченные кванторы, и постройте их отрицания:

0) Теорема Фейера о суммировании средними арифметическими.

Каждый ряд Фурье суммируем средними арифметическими к функции f(t) при всех t в интервале (-T/2, T/2), для которых функция f(t) непрерывна; в точках разрыва первого рода средние арифметические сходятся к (f(t – 0) + f(t + 0))/2

1) Теорема Вейерштрасса об изолированной особой точке.

Пусть f(z) – однозначная функция, имеющая изолированную особую точку при z = a. Тогда для любого комплексного числа А (включая А = ¥) существует последовательность точек z_k ® a такая, что lim f(z_k) = A
при k ® ¥.

2) Теорема Пикара об изолированной особой точке.

Пусть f(z) – однозначная функция, имеющая изолированную особую точку при z = a. Тогда для любого комплексного числа А ¹ ¥, за исключением, быть может, одного значения А = А₀ , каждая окрестность точки а содержит бесконечное множество точек z таких, что f(z) = A.

3) Теорема Лагранжа о конечном приращении.

Если функция f(x) непрерывна на [a, b] и дифференцируема на (a, b), то в интервале (a, b) существует такое число X, что f(b) – f(a) = f’(X)(b – a).

4) Теорема Вейерштрасса о приближении.

Пусть f(x) – действительная функция, непрерывная на ограниченном замкнутом интервале [a, b]. Тогда для каждого заданного положительного числа e существует такой действительный многочлен

P(x)º 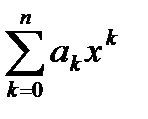, что êf(x) – P(x) ê<e при всех x Î [a, b].

5) Теорема Коши о среднем значении

Если функции u(x) и v(x) непрерывны на [a, b] и v(b) ¹ v(a) и существуют производные u’(x) и v’(x) в интервале (a, b) и одновременно не обращаются в нуль, то в интервале (a, b) существует такое число X, что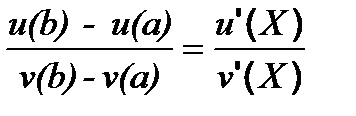

6) Теорема Руше о нулях функции

Если f₁(z) и f₂(z) – аналитические функции в ограниченной области D и на ее контуре C и если | f₂(z)| < | f₁(z)| ¹ 0 на С, то функции f₁(z) и f₁(z) + f₂(z) имеют одинаковое число нулей в области D.

7) Теорема о функциях, разложимых в ряд Фурье

Ряд Фурье или интеграл Фурье, порожденный действительной функцией f(t), абсолютная величина которой интегрируема на интервале разложения I, сходится равномерно к f(t) на каждом таком интервале
(a, b) Ì (a - d, b + d) Ì I, где d > 0, что на (a - d, b + d) функция f(t) непрерывна.

8) Теорема Фейера о cходимости средних арифметических.

Средние арифметические сходятся к f(t) почти всюду в интервале разложения; они сходятся к f(t) равномерно на каждом таком интервале
(a, b)

9) Теорема Ролля об отделении действительных корней

Пусть a и b – два соседних действительных корня уравнения f’(x) = 0 и пусть f(a) ¹ 0 и f(b) ¹ 0. Уравнение f(x) = 0 между a и b либо вовсе не имеет действительных корней, либо имеет один действительный корень в зависимости от того, будут ли числа f(a) и f(b) иметь одинаковые или противоположные знаки.

Глава 4. Элементы теории алгоритмов

4.1.Практическое занятие №14. Способы описания
алгоритмов.

К основным изобразительным средствам алгоритмов можно отнести следующие способы записи:

- словесная;

- словесно-формульная;

- в графическом виде (в виде блок-схем);

- в виде текста программы на алгоритмическом языке.

Примеры выполнения заданий

1. Опишите в словесной форме алгоритм вычисления значения логической функции, реализующую операцию конъюнкции:

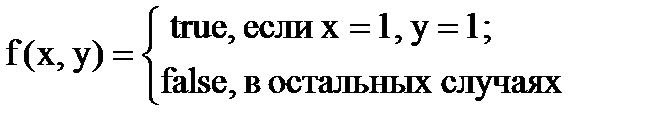
Решение.

1. Ввести значения аргументов x и y. Перейти к п. 2.

2. Проверить, x равно 1 и y равно 1? Если да, то выдать сообщение: ‘Значение функции равно true’, перейти к п. 4, иначе перейти к п. 3.

3. Проверить, x равно 1 и y равно 0 или x равно 0 и y равно 1 или x равно 0 и y равно 0? Если да, то выдать сообщение: ‘Значение функции равно false’, перейти к п. 4, иначе выдать сообщение об ошибке ввода.

4. Завершить процесс.

2. Опишите пример 1 в словесно-формульной форме.

1. Ввести значения аргументов x и y. Перейти к п. 2.

2. Проверить, x = 1 и y = 1? Если да, то выдать сообщение: ‘Значение функции равно true’, перейти к п. 4, иначе перейти к п. 3.

3. Проверить, x = 1 и y = 0 или x = 0 и y = 1 или x = 0 и
y = 0? Если да, то выдать сообщение: ‘Значение функции равно false’, перейти к п. 4, иначе выдать сообщение об ошибке ввода.

4. Завершить процесс.

3. Опишите пример 1 в виде текста программы на алгоритмическом языке.

Program func;

var x, y: integer;

begin

writeln (‘Введите значения двух аргументов функции (0/1)’); readln (x, y);

if (x = 1) and (y = 1) then write (‘Значение функции равно true’);

if (x = 1) and (y = 0) or (x = 0) and (y = 1) or (x = 0) and (y = 0)

then write (‘Значение функции равно false’)

else write (‘Ошибка ввода‘)

end.

5. Опишите пример 1 в виде блок-схемы

x, y

Начало

x=1 & y=1?

Да

Нет

(x=1)&(y=0)? r (x=0)&(y=1)? (x=0)&(y=0)?

Окончание

Ошибка ввода

F(x,y)= true

Да

Нет

F(x,y)= false

Задания для самостоятельного выполнения

1. Опишите алгоритмы в словесной форме:

1. Переменной d присваивают длину окружности, площадь круга и объем шара одного и того же заданного радиуса.

2. Даны произвольные числа a, b, c. Если нельзя построить треугольник с такими длинами сторон, то напечатать 0, иначе напечатать 3 - если треугольник равносторонний, 2 - если треугольник равнобедренный или 1 - в противном случае.

3. Даны целые числа k и m, действительные числа x, y, z. При
k < m², k = m² или k > m², замените модулем соответственно значения x, y, z., а два других уменьшить на 0.5.

2. Опишите алгоритмы в словесно-формульной форме:

1. Даны два числа а и в. Обменяйте их значениями, не используя третьей переменной.

2. Для заданного числа a найдите корень уравнения f(x)=0, где:

.

3. Найдите корни квадратного уравнения, если заданы коэффициенты а, в, с.

4. Вычислите площадь треугольника по заданным сторонам, если это возможно.

5. Даны действительные числа x, y, z. Вычислите: max (min (y + z, x * y), y + e^x).

6. Дано число а. Определите первый отрицательный член и его номер в последовательности x₁, x₂, …x_n, где x₁=a, x_n=tg (x_n-1).

Дата добавления: 2014-11-20