За допомогою векторів

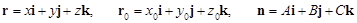
запишемо рівняння площини у векторній формі:

,

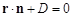або

Розглянемо функцію трьох змінних

.

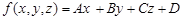За допомогою цієї функції увесь простір можна розбити на два півпростори: в одному виконується нерівність , а в іншому — нерівність 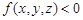. На площині, яка розмежовує ці підпростори, виконується рівність .

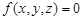3.5.2. Дослідження загального
рівняння площини

Якщо одна з координат х, у, z не входить до рівняння поверхні , то зі зміною цієї координати вид поверхні не змінюється. Така поверхня буде циліндричною із твірною, що паралельна осі, яка відповідає зазначеній координаті.

Дамо інтерпретацію загального рівняння площини

в разі, якщо один або кілька його коефіцієнтів перетворюються на нуль.

1. А = 0 — площина паралельна осі х.

2. В = 0 — площина паралельна осі у.

3. С = 0 — площина паралельна осі z.

4. D = 0 — площина проходить через початок координат.

5. А = 0, В = 0 — площина перпендикулярна до осі z.

6. А = 0, С = 0 — площина перпендикулярна до осі у.

7. В = 0, С = 0 — площина перпендикулярна до осі х.

8. А = 0, D = 0 — площина проходить через вісь х.

9. В = 0, D = 0 — площина проходить через вісь у.

10. С = 0, D = 0 — площина проходить через вісь z.

11. А = 0, В = 0, D = 0 — площина проходить через осі х, у.

12. А = 0, С = 0, D = 0 — площина проходить через осі х, z.

13. В = 0, С = 0, D = 0 — площина проходить через осі у, z.

У загальному випадку, коли жодний із коефіцієнтів рівняння не перетворюється на нуль, рівняння площини можна звести до вигляду

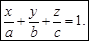(1)

Площина, що визначається рівнянням (1), перетинає осі координат у точках х = а, у = b, z = c. Тому рівняння (1) називається рівнянням площини у відрізках на осях.

Зведемо рівняння площини

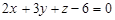
до вигляду (1). Для цього поділимо обидві його частини на 6:

.

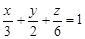Отже, площина перетинає осі координат у точках х = 3, у = 2, z = 6. ·

3.5.3. Рівняння площини,
що проходить через три точки

Нехай дано три точки М ₁(х ₁, у ₁, z ₁), М ₂(х ₂, у ₂, z ₂), М ₃(х ₃, у ₃, z ₃), які не лежать на одній прямій. Знайдемо рівняння площини, яка проходить через ці три точки. Записавши рівняння

складемо систему:

Оскільки ця однорідна система рівнянь має ненульовий розв’язок А, В, С, то її визначник дорівнює нулю:

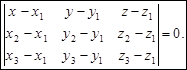(1)

1. Рівняння (1) є рівнянням площини, що проходить через три точки.

¨ Справді, рівняння (1) є лінійним і, відповідно, визначає деяку площину. Точки лежать на цій площині, оскільки при підставлянні 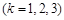у визначник (1) дістанемо визначник з нульовим рядком або двома однаковими рядками.

Запишемо рівняння площини, яка проходить через три точки М ₁(1, 1, 1), М ₂(2, 3, 4), М ₃(4, 3, 1).

· Рівняння (1) набирає вигляду:

.

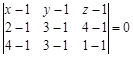Розкривши визначник, дістанемо рівняння

. ·

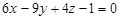3.5.4. Відстань від точки до площини

Дано площину

і точку М ₁(х ₁, у ₁, z ₁) поза нею. Знайдемо відстань від точки М ₁ до площини. Нехай точка М ₀(х ₀, у ₀, z ₀) лежить на площині. Тоді відстань d від точки М ₁ до площини дорівнює модулю проекції вектора , на нормаль до площини (рис. 3.50).

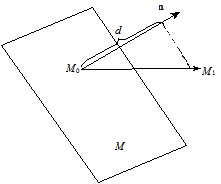
Рис. 3.50

Отже,

.

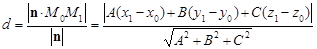Оскільки

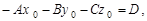
то

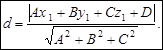(1)

Знайдемо відстань d від точки М ₁(1, 2, 3) до площини, заданої рівнянням .

· Згідно з (1) маємо:

. ·

Рівняння площини, записане у вигляді

де знак перед радикалом протилежний знаку D, називається нормальним рівнянням площини. Якщо D = 0, то вибір знака неістотний.

Щоб знайти відстань від точки М ₁(х ₁, у ₁, z ₁) до площини, слід підставити координати цієї точки в нормальне рівняння площини і знайти модуль здобутої величини.

Величина

називається відхиленням точки М(х, у, z) від площини.

Модуль відхилення дорівнює відстані від точки М(х, у, z) до площини. Якщо 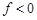, то точка М(х, у, z) і початок координат лежать по один бік від розглядуваної площини; якщо 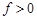, — по різні боки; якщо , то М лежить на цій площині.

Коли маємо дві площини, які перетинаються й подаються рівняннями

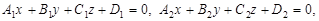
то бісектральні площини визначаються рівнянням

(2)

3.5.5. Взаємне розміщення двох площин

Нехай дано дві площини, які визначаються загальними рівняннями

.

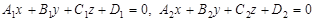Розглянемо вектори нормалей до кожної з площин:

.

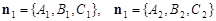Кут q між площинами визначається кутом q між векторами 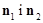. Отже, справджується рівність

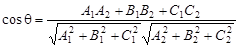. (1)

Умова перпендикулярності площин така:

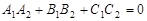. (2)

Умова паралельності площин:

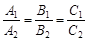. (3)

Дата добавления: 2014-11-20