
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания
|
|
|
|
Тема 7. Ряды динамики
1. Понятие и виды рядов динамики.
2. Средняя хронологическая.
3. Абсолютные показатели динамики.
4. Относительные показатели динамики.
5. Сравнительный анализ нескольких рядов динамики.
6. Методы выявления основной тенденции ряда динамики.
7. Прогнозирование (экстраполяция) на основе рядов динамики.
Это тоже одна из центральных тем теории статистики. Вначале здесь необходимо усвоить понятие ряда динамики, его элементов, видов рядов динамики (прежде всего интервальных и моментных рядов). Абсолютные показатели динамики (абсолютный прирост, средний абсолютный прирост) и относительные (темп роста, темп прироста, средний темп роста, средний темп прироста). Следует обратить внимание на формулы названных показателей динамики и их экономическую интерпретацию, взаимосвязь темпов роста и темпов прироста. Нужно усвоить, что средний темп роста можно вычислять по одной из трех формул и нельзя вычислять по формуле средней арифметической. Самостоятельное место занимает показатель – абсолютное содержание одного процента прироста, широко используемый в анализе.
При изучении этой темы необходимо обратить внимание на методы выявления основной тенденции динамического ряда (сглаживание с помощью скользящей средней и аналитическое выравнивание) и области их практического применения.
При работе с темой необходимо изучить методы выявления основной тенденции динамического ряда (метод укрупнения интервалов, сглаживание по методу скользящей средней и аналитическое выравнивание) и области их практического применения.
Для успешного усвоения темы 7 необходимо ознакомиться с представленным теоретическим материалом и целесообразно решить предлагаемые задачи.
Ряд динамики (динамический ряд) – ряд чисел, характеризующих изменение социально-экономического явления во времени.
Элементы ряда динамики:
1) последовательные периоды времени или моменты времени,
2) числовые значения изучаемого показателя, относящиеся к этим периодам или моментам времени, которые называются уровнями ряда (у).
Выделяют крайние (начальный 
 и конечный
и конечный  ) и промежуточные уровни ряда динамики.
) и промежуточные уровни ряда динамики.
Общая схема ряда динамики
| Период времени (год) | Уровень ряда |
 
| |

| |

| |

|
Динамические ряды классифицируются по ряду признаков.
По способу получения динамические ряды делятся на первичные (полученные путем подсчета итогов в результате наблюдения или сводки) и производные (полученные расчетным путем).
В зависимости от вида показателя (его статистической природы) динамические ряды делятся на ряды абсолютных, относительных и средних величин.
В зависимости от времени, к которому относятся уровни ряда, различают интервальные и моментные ряды.
Интервальными называются ряды, уровни которых характеризуют изменение явления за определенный период времени (месяц, квартал, год и т.п.). Например, ряд, характеризующий динамику добычи газа за пятилетие.
Особенностью таких рядов является то, что в них уровни ряда не содержат повторный счет и их можно суммировать для рядов абсолютных величин.
Моментными называются ряды, уровни которых характеризуют изменение явления на конкретный момент времени (на дату). Например, ряд, характеризующий динамику численности населения на начало каждого месяца.
Особенностью таких рядов является то, что в них уровни ряда содержат повторный счет и их суммировать нельзя, т.к. это не имеет экономического смысла.
Для обобщающей характеристики динамического ряда рассчитываются средние хронологические, методы расчета которых зависят от вида динамического ряда.
Среднюю хронологическую для интервального ряда с равным интервалом рассчитывают как простую среднюю арифметическую из уровней ряда:
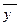 =
=  ,
,
где  – средний уровень ряда (средняя хронологическая);
– средний уровень ряда (средняя хронологическая);
 – отдельный уровень ряда;
– отдельный уровень ряда;
n – число уровней (соответствует периоду времени).
Среднюю хронологическую для моментного ряда с равноотстоящими уровнями рассчитывают по следующей формуле:

 .
.
Эта формула получена путем приближенного интегрирования по методу трапеций. Средняя хронологическая для моментного ряда равна отношению суммы половинных значений крайних уровней и суммы полных значений промежуточных уровней к числу уровней без одного.
Для рядов с неравноотстоящими уровнями используют формулу средней хронологической взвешенной:
 ,
,
где  – средний уровень ряда за какой-либо период времени между двумя соседними датами (например, за январь, …, за второй квартал и т.п.);
– средний уровень ряда за какой-либо период времени между двумя соседними датами (например, за январь, …, за второй квартал и т.п.);
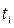 – продолжительность периода времени между двумя соседними датами в соответствующих единицах времени (число месяцев, число дней и т.д). Этот показатель выступает в качестве весов средней.
– продолжительность периода времени между двумя соседними датами в соответствующих единицах времени (число месяцев, число дней и т.д). Этот показатель выступает в качестве весов средней.
Для количественной характеристики изменения социально-экономических явлений во времени статистика использует абсолютные (абсолютный прирост, средний абсолютный прирост) и относительные (темп роста, темп прироста, средний темп роста, средний темп прироста) показатели динамики. (формулы их расчета приведены в типовой задаче №2 данной темы).
Абсолютные показатели измеряют абсолютную скорость изменения уровней динамического ряда во времени (месяц, квартал, год и т.д.) их измеряют в тех же единицах, что и имеющиеся уровни ряда. О тносительные показатели характеризуют интенсивность (относительную скорость) изменения уровней динамического ряда во времени. Они выражаются в форме коэффициента (при вычислениях) или в процентах (в анализе). Они отвечают на вопрос, во сколько раз или на сколько процентов изменяется уровень ряда за изучаемый период времени.
На изменение уровня ряда динамики влияют различные факторы: систематические и случайные. Для устранения случайных факторов и выявления основной тенденции развития используют метод укрупнения интервалов, сглаживание по методу скользящей средней и аналитическое выравнивание по методу наименьших квадратов. Отметим, что под общей тенденцией понимают стремление уровней динамического ряда к росту, снижению или стабильности.
Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдаются снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. Поэтому для наглядного представления тренда применяется метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т. д.
Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя.
Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода.
Для каждого конкретного ряда динамики (у1, у2,..., уn) расчет скользящей средней производится в следующем порядке:
1) определите интервал сглаживания, т.е. число входящих в него уровней m, используя правило: если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берут по возможности большим и, наоборот, интервал сглаживания уменьшают, когда нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний;
2) вычислите среднее значение уровней, образующих интервал сглаживания, которое одновременно является сглаживающим значением уровня, находящегося в центре интервала сглаживания.
Обратите внимание, что определение скользящей средней по четному числу членов ряда динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания.
Если число членов скользящей средней обозначить через 2m, то серединным будет уровень, относящийся к m + 1/2 члену ряда, т. е. имеет место сдвиг периода, к которому относится уровень. Например, средняя, найденная для четырех членов, относится к середине между вторым и третьим периодами, следующая средняя – к середине между третьим и четвертым и т. д. Чтобы ликвидировать такой сдвиг, применяют так называемый способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. При центрировании необходимо находить скользящие суммы, скользящие средние нецентрированные по этим суммам и средние из двух смежных нецентрированных скользящих средних;
3) сдвиньте интервал сглаживания на один уровень вправо, потом вычислить сглаженное значение для t + 1 члена ряда, снова произвести сдвиг и т. д.
Аналитическое выравнивание рядов динамики, в отличие от метода скользящей средней, учитывает закономерность изменения основной тенденции развития явления и поэтому является более совершенным методом. Он основан и на описании тенденции с помощью определённой математической функции.
Процесс аналитического выравнивания включает два этапа:
1) выбор вида кривой, форма которой соответствует характеру изменения динамического ряда;
2) определение параметров функции и выравнивание значения уровней ряда.
Выбор вида кривой производится с помощью графика, на котором по фактическим данным строится эта кривая. Затем она графически или другими способами оценивается, и выбирается наиболее подходящая кривая, которая называется трендом. Во всех случаях окончательно выбранная кривая должна удовлетворять методу наименьших квадратов:
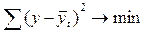 ,
,
где y – фактические уровни ряда;
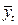 – выравнивание, т.е. теоретические уровни для каждого периода t.
– выравнивание, т.е. теоретические уровни для каждого периода t.
На втором этапе определяются параметры функции, например прямой 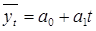 , с помощью системы нормальных уравнений. Определив параметры а0 и а1, подставляют их значение в уравнение
, с помощью системы нормальных уравнений. Определив параметры а0 и а1, подставляют их значение в уравнение 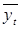 , где t – время (t =1, 2, …, n).
, где t – время (t =1, 2, …, n).
Аналитическое выравнивание позволяет не только выявить общее направление основной тенденции, но и дать числовую характеристику изменения динамического ряда в виде показателей средней скорости изменения уровня (а1), что используется при экстраполяции динамических рядов.
Предположим, что выравнивание производится по прямой:

Далее находим частные производные и решаем систему уравнений:
 .
.
Одна из задач статистики – прогнозирование возможных значений уровней динамического ряда. Эта задача решается, в частности, на основе статистических методов экстраполяции. Под экстраполяцией понимается приближенный расчет неизвестных уровней динамического ряда, лежащих за его пределами. При осуществлении экстраполяции на основе тренда – это математическое нахождение по ряду данных значений функции других ее значений, находящихся вне этого ряда.
При экстраполяции исходят из предположения, что закономерность развития, имевшая место в течение известного периода, сохранится также и в будущем (перспективная экстраполяция – прогнозирование) или имела место в прошлом (ретроспективная экстраполяция).
Важное значение при экстраполяции имеют вопросы о ее базе расчета и сроках прогнозирования. База расчета, определяемая на основе теоретического анализа сущности изучаемого явления, должна быть оптимальной по своей длительности. В качестве такой базы нельзя использовать очень короткий или очень длинный период. При экстраполяции на практике берут те субпериоды базисного ряда динамики, которые составляют определенный этап в развитии изучаемого явления в конкретных исторических условиях. Установление сроков прогнозирования зависит от задачи исследования. Но следует иметь в виду, что чем короче сроки прогноза, тем надежнее результаты экстраполяции. Обычно рекомендуют, чтобы срок прогноза не превышал одной трети базы расчета.
Применение методов экстраполяции зависит от характера изменений в базисном ряду динамики и предопределяется постановкой задачи исследования. Экстраполяция может производиться:
1) на основе среднего (постоянного) абсолютного прироста ( ):
):
 ,
,
где  – экстраполируемый уровень,
– экстраполируемый уровень,
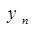 – конечный уровень базисного ряда динамики,
– конечный уровень базисного ряда динамики,
t – срок прогноза;
2) на основе среднего (годового, стабильного) темпа роста:
 ;
;
3) на основе аналитического выравнивания применяется адекватная трендовая модель. Так, например, при выравнивании по прямой объема производства картофеля в районе за 1999-2006 гг. была определена на основе функции трендовая модель:
 .
.
Если начало отсчета времени в 1999 г. было принято за 1, то для прогнозирования возможного объема производства картофеля в районе в 2007 г. в модель подставляется t =9 (9 значение с начала отсчета):
 .
.
Для закрепления теоретического материала целесообразно решить следующие задачи.
Типовая задача 1
Товарные запасы магазина на начало квартала составили (тыс. ден. ед.):
| на 1.01.2004 г. | на 1.04.2004 г. | на 1.07.2004 г. | на 1.10.2004 г. | на 1.01.2005 г. |
| 75,2 | 70,8 | 90,0 | 80,5 | 70,0 |
Определите средние запасы материалов: а) за первое и второе полугодия; б) за год (непосредственно по исходным данным и по вычисленным полугодовым данным).
Выбор конкретной формулы для расчета зависит от вида ряда динамики. В нашем случае динамика товарных запасов представлена на конкретную дату (на 1-ое число), следовательно, ряд является моментным. Так как период, за который имеются данные везде одинаков (равен 1-му кварталу), то уровни ряда являются равноотстоящими. Соответственно, средние товарные запасы за первое, второе полугодия и год определяются следующим образом.
Средние товарные запасы за первое полугодие:

 = 76,7 тыс. ден. ед.
= 76,7 тыс. ден. ед.
Средние товарные запасы за первое полугодие составили 76,7 тыс. ден. ед.
Средние товарные запасы за второе полугодие:

 = 80,3 тыс. ден. ед.
= 80,3 тыс. ден. ед.
Средние товарные запасы за второе полугодие составили 80,3 тыс. ден. ед.
Средние товарные запасы за год:
 =
=  = 78,5 тыс. ден. ед.
= 78,5 тыс. ден. ед.
Средние запасы можно исчислить и по найденным полугодовым уровням. В этом случае следует использовать формулу простой средней арифметической из уровней ряда, так как полученные полугодовые уровни относятся уже не к конкретному моменту времени, а приведены за период (полугодие). Следовательно, при расчете среднего запаса материалов за год по найденным полугодовым уровням получим:
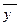 =
=  тыс. ден. ед.
тыс. ден. ед.
Таким образом, средний запас материалов за год составил 78,5 тыс. ден. ед.
Типовая задача 2
Общая площадь аварийного и ветхого жилищного фонда города составила (тыс.кв.м.):
| 2002 г. | 2003 г. | 2004 г. | 2005 г. |
Определите для общей площади аварийного и ветхого жилищного фонда города:
1) цепные и базисные абсолютные приросты;
2) цепные и базисные темпы роста;
3) цепные и базисные темпы прироста;
4) средний годовой абсолютный прирост за 2003 –2005 гг.;
5) средний годовой темп роста и средний годовой темп прироста за 2003 –2005 гг.;
6) абсолютное значение одного процента прироста за каждый год (по сравнению с предыдущим).
1. В общем виде абсолютный прирост – это разность между последующим и предшествующим уровнями ряда (разность двух уровней).
Различают цепные и базисные абсолютные приросты. При построении этих и последующих показателей динамики удобнее нумеровать уровни ряда, начиная с  , далее
, далее  ;
;  ;
;  ;…;
;…;  ;
;  .
.
Цепные (ежегодные) (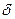 ) абсолютные приросты (с переменной базой сравнения) вычисляют как разность между уровнями ряда и предыдущим уровнем
) абсолютные приросты (с переменной базой сравнения) вычисляют как разность между уровнями ряда и предыдущим уровнем  :
:
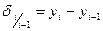 (
( =1, 2,…, n).
=1, 2,…, n).
Значит, для 2003 г. по сравнению с 2002 г. абсолютный прирост составит:  =7 тыс.кв.м., для 2004 г. –
=7 тыс.кв.м., для 2004 г. –  =13 тыс.кв.м., для 2005 г. соответственно 15 тыс.кв.м. Таким образом, в 2005 г. по сравнению с 2004 г. общая площадь аварийного и ветхого жилищного фонда города выросла на 15 тыс.кв.м.
=13 тыс.кв.м., для 2005 г. соответственно 15 тыс.кв.м. Таким образом, в 2005 г. по сравнению с 2004 г. общая площадь аварийного и ветхого жилищного фонда города выросла на 15 тыс.кв.м.
Базисные ( ) абсолютные приросты (с постоянной базой сравнения) вычисляют путем вычитания из каждого последующего
) абсолютные приросты (с постоянной базой сравнения) вычисляют путем вычитания из каждого последующего  -го уровня одного и того же уровня
-го уровня одного и того же уровня  , принятого за базу сравнения:
, принятого за базу сравнения:
 (1, 2,…, n).
(1, 2,…, n).
Значит, для 2003 г., по сравнению с 2002 г. абсолютный прирост общей площади аварийного и ветхого жилищного фонда города составит:  =7 тыс.кв.м., для 2004 г. по сравнению с 2002 г.
=7 тыс.кв.м., для 2004 г. по сравнению с 2002 г. 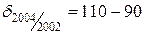 = 20 тыс.кв.м. и соответственно для 2005 г. 35 тыс.кв.м.
= 20 тыс.кв.м. и соответственно для 2005 г. 35 тыс.кв.м.
Таким образом, в 2005 г. по сравнению с 2002 г. общая площадь аварийного и ветхого жилищного фонда города выросла на 35 млн ден. ед.
Если взять абсолютный прирост за весь период, ограничивающий динамический ряд, то получим формулу:
 ,
,
где  – сравниваемый уровень;
– сравниваемый уровень;
 – базисный уровень.
– базисный уровень.
Заметим, если разности получаются в процессе вычислений с отрицательным значением, то правильнее называть показатели абсолютным снижением уровня ряда.
Установлено, что между базисным и цепными абсолютными приростами существует связь:
 .
.
То есть базисный абсолютный прирост за какой-либо период равен сумме последовательных цепных абсолютных приростов за тот же период. Эта связь позволяет определять базисный абсолютный прирост другим способом – на основе цепных абсолютных приростов. Проверим это: 7 + 13 + 15 = 35 тыс.кв.м.
2. В общем виде темп роста (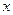 ) – это отношение последующего уровня к предшествующему (т.е. отношение двух уровней).
) – это отношение последующего уровня к предшествующему (т.е. отношение двух уровней).
Темпы роста, рассчитанные по приведенным ниже формулам, выражаются в форме коэффициента. Если полученные результаты умножить на 100, получим темпы роста, выраженные в процентах. Последняя форма выражения темпов роста применяется чаще.
Темп роста (снижения) показывает, во сколько раз уровень рассматриваемого периода больше уровня предыдущего или базисного, или какую часть его составляет. При увеличении уровня явления в отчетном периоде по сравнению с базисным темп роста будет больше 1 (100%), при уменьшении – меньше.
Различают темпы роста цепные и базисные.
Цепные темпы роста ( ) рассчитывают как отношение последующего уровня к предшествующему:
) рассчитывают как отношение последующего уровня к предшествующему:
 (
( =1, 2,…, n).
=1, 2,…, n).
Значит, темп роста для 2003 г. по сравнению с 2002 г. составит:  =1,077 или 107,7%, для 2004 г.
=1,077 или 107,7%, для 2004 г.  =113,4%, а для 2005 г. 113,6%.
=113,4%, а для 2005 г. 113,6%.
Таким образом, в 2005 г. по сравнению с 2004 г. общая площадь аварийного и ветхого жилищного фонда города увеличилась на 13,6%.
Базисные темпы роста ( ) рассчитывают как последовательное отношение уровней ряда к одному и тому же уровню, принятому за базу сравнения (базисному уровню):
) рассчитывают как последовательное отношение уровней ряда к одному и тому же уровню, принятому за базу сравнения (базисному уровню):
 (
( =1, 2,…, n).
=1, 2,…, n).
Темп роста для 2003 г. по сравнению с 2002 г. составит:
 =107,7%, для 2004 г., по сравнению с 2002 г.
=107,7%, для 2004 г., по сравнению с 2002 г.  =122,2 %, а для 2005 г. соответственно составит 138,8%.
=122,2 %, а для 2005 г. соответственно составит 138,8%.
Таким образом, в 2005 г. по сравнению с 2002 г. общая площадь аварийного и ветхого жилищного фонда города увеличилась на 38,8%.
Базисный темп роста за весь период, ограничивающий динамический ряд, записывается так:
 .
.
Установлена взаимосвязь между базисными и цепнымитемпами роста:
 .
.
Базисный темп роста всего динамического ряда равен произведению последовательных цепных темпов роста. Эта взаимосвязь позволяет определять базисные темпы роста на основе цепных и наоборот. Осуществим проверку: 1,077 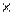 1,134
1,134 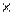 1,136 = 1,388.
1,136 = 1,388.
3. Темп прироста ( ), или относительный прирост, рассчитывается в общем виде как отношение абсолютного прироста к базисному уровню ряда, т.е.
), или относительный прирост, рассчитывается в общем виде как отношение абсолютного прироста к базисному уровню ряда, т.е.
 .
.
Темп прироста, как и темп роста, может быть цепным или базисным и выражается в коэффициентах или в процентах. Темп прироста показывает, на сколько долей единиц или процентов увеличился (+) или уменьшился (-) уровень отчетного периода по сравнению с базисным.
Приведенная формула темпа прироста может быть преобразована в более простую, показывающую, что между темпами прироста и темпами роста существует взаимосвязь:  , т.е. темп прироста равен темпу роста, уменьшенному на 1 (или на 100%, если темпы роста выражены в процентах).
, т.е. темп прироста равен темпу роста, уменьшенному на 1 (или на 100%, если темпы роста выражены в процентах).
Таким образом, зная темпы роста, всегда можно определить темпы прироста и наоборот. Докажем это. Цепной темп прироста составит: 107,7 – 100 = 7,7%; 113,4 – 100 = 13,4%; 113,6 – 100 = 13,6%. Базисный темп прироста составит: 107,7 – 100 = 7,7%; 122,2 – 100 = 22,2%; 138,8 – 100 = 38,8%.
Выводы по темпам прироста аналогичны выводам по темпам роста.
4. Средний абсолютный прирост ( ) может быть рассчитан по одной из двух формул. В основе первой формулы – связь между базисным и цепными абсолютными приростами:
) может быть рассчитан по одной из двух формул. В основе первой формулы – связь между базисным и цепными абсолютными приростами:
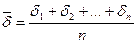 ,
,
где  ;
;  ;…;
;…;  – цепные абсолютные приросты;
– цепные абсолютные приросты;
 – число абсолютных приростов или период времени, за который рассчитывается средний абсолютный прирост.
– число абсолютных приростов или период времени, за который рассчитывается средний абсолютный прирост.
Соответственно получим: 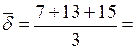 11,7 тыс.кв.м.
11,7 тыс.кв.м.
Средний абсолютный прирост представляет собой среднюю арифметическую простую из цепных абсолютных приростов.
Вторая, чаще используемая на практике, формула:
 =
= 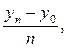
где  – конечный уровень ряда;
– конечный уровень ряда;
 – начальный (базисный) уровень ряда;
– начальный (базисный) уровень ряда;
 – период времени, ограничивающий ряд.
– период времени, ограничивающий ряд.
 =
=  тыс.кв.м.
тыс.кв.м.
Средний абсолютный прирост показывает, что ежегоднона 11,7 тыс.кв.м. в среднем увеличивается общая площадь аварийного и ветхого жилищного фонда города.
5. Средний (годовой) темп роста (снижения) (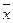 ) может быть определен по одной из трех формул, в основе которых темп роста.
) может быть определен по одной из трех формул, в основе которых темп роста.
Исходной формулой является средняя геометрическая из последовательных цепных темпов роста:
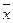 =
= 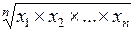 ,
,
где  ;
;  ;…;
;…;  – цепные (ежегодные) темпы роста (снижения), выраженные в коэффициентах,
– цепные (ежегодные) темпы роста (снижения), выраженные в коэффициентах,
 – период времени, за который рассчитывается средний (годовой) темп роста, соответствующий числу цепных темпов роста.
– период времени, за который рассчитывается средний (годовой) темп роста, соответствующий числу цепных темпов роста.
В итоге получим: 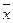 =
=  111,5%
111,5%
Так как произведение последовательных цепных темпов роста равно базисному темпу роста, можно использовать следующую формулу для определения среднего (годового) темпа роста:
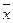 =
=  ,
,
где  – конечный уровень ряда;
– конечный уровень ряда;
 – базисный уровень ряда;
– базисный уровень ряда;
 – период времени, ограничивающий динамический ряд (или число уровней ряда без одного, принятого за базу сравнения).
– период времени, ограничивающий динамический ряд (или число уровней ряда без одного, принятого за базу сравнения).
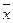 =
=  111,5%.
111,5%.
Последняя формула среднего темпа роста применяется наиболее часто, так как для расчета необходимо знать только величину крайних уровней ряда.
Для расчета среднего (годового) темпа роста пользуются современной вычислительной техникой или специальными таблицами.
Средний (годовой) темп роста показывает, что за изучаемый период в 1,115 раз ежегодно за изучаемый период увеличивается общая площадь аварийного и ветхого жилищного фонда города.
Средний (годовой) темп прироста  рассчитывают только с помощью среднего темпа роста, его нельзя определить непосредственно по данным о цепных темпах прироста. Средний темп прироста:
рассчитывают только с помощью среднего темпа роста, его нельзя определить непосредственно по данным о цепных темпах прироста. Средний темп прироста:  или
или 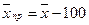 .
.
Первая формула используется, если средний темп роста (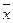 ) выражен в коэффициентах, вторая – если он выражен в процентах:
) выражен в коэффициентах, вторая – если он выражен в процентах:  =111,5 – 100 = 11,5%.
=111,5 – 100 = 11,5%.
Выводы по средним годовым темпам роста и средним годовым темпам прироста аналогичны выводам по темпам роста.
6. Абсолютное значение 1% прироста широко используется в экономическом анализе, так как позволяет ответить на вопрос, какие абсолютные по своему размеру величины скрываются за большими или малыми темпами роста и прироста, т.е. каково абсолютное содержание 1% прироста. Этот показатель (обозначим его a) рассчитывается как отношение абсолютного прироста ( ) к темпу прироста за этот же период, выраженному в процентах (
) к темпу прироста за этот же период, выраженному в процентах ( ):
):
 .
.
Соответственно получим для периода с 2002 по 2003 гг.  тыс.кв.м.; для периода с 2003 по 2004 гг.
тыс.кв.м.; для периода с 2003 по 2004 гг.  тыс.кв.м.; для периода с 2004 по 2005 гг.
тыс.кв.м.; для периода с 2004 по 2005 гг.  тыс.кв.м.
тыс.кв.м.
Этот показатель можно рассчитать и по преобразованной формуле:
 ,
,
т.е. путем деления предыдушего уровня ряда на 100.
 тыс.кв.м.;
тыс.кв.м.;  тыс.кв.м.;
тыс.кв.м.; 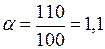 тыс.кв.м.
тыс.кв.м.
Следует отметить, что с 2004 по 2005 гг. в 1 % прироста содержится 1,1тыс. кв.м. общей площади аварийного и ветхого жилищного фонда города.
Заметим, что по данной формуле расчет абсолютного значения 1% прироста имеет смысл только для цепных абсолютных приростов и темпов прироста. Для базисных показателей он будет одним и тем же для всех лет, так как первоначальный уровень остается неизменным.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 1426; Нарушение авторских прав?; Мы поможем в написании вашей работы!