Методические указания. Тема 9. Статистическое изучение связи между признаками

Тема 9. Статистическое изучение связи между признаками

1. Виды и формы связей.

2. Методы изучения связи.

3. Оценка тесноты связи.

При изучении связей различают факторные и результативные признаки. Факторные – это признаки, влияющие на изменение других признаков, т.е. выступающие в качестве аргумента. Результативные – это признаки, которые зависят от факторных и изменяются под их воздействием, т.е. выступающие в качестве функции.

В зависимости от направления действия связи могут быть прямые (положительные) и обратные (отрицательные). Связь называется прямой, если направление изменения результативного признака совпадает с направлением изменения факторного признака. Если же с увеличением факторного признака результативный признак уменьшается, то такие связи называются обратными.

По характеру зависимости между признаками различают два вида связей: функциональные и корреляционные.

Функциональная связь – это такая связь, при которой каждому значению факторного признака соответствует строго определенное значение результативного признака. Функциональная связь характеризуется полным соответствием между названными признаками. Функциональную связь можно представить в виде уравнения:

,

где x – факторный признак;

y – результативный признак.

Заметим, что факторных признаков может быть несколько.

Корреляционная связь – это такая связь, когда одному и тому же значению факторного признака могут соответствовать различные значения результативного, при этом с изменением факторного признака изменяется средняя величина результативного признака.

Корреляционная связь возникает в тех случаях, когда на результативный признак действует, помимо изучаемого фактора, множество других, от влияния которых абстрагируются. Особенности корреляционной связи в том, что они обнаруживаются не в единичных случаях, а в массе, в среднем, и в том, что это неполные, приближенные связи. Корреляционную связь можно выразить уравнением:

,

где x – факторный признак,

– среднее значение результативного признака, сформировавшееся под действием всех факторов.

По аналитическому выражению (форме) связи могут быть прямолинейные и криволинейные. Связь называется прямолинейной (линейной), если зависимость результативного признака от факторного может быть выражена уравнением прямой линии. Связь называется криволинейной, если зависимость между признаками выражается уравнением какой-либо кривой (параболы, гиперболы и др.)

В зависимости от числа определяющих признаков связи делятся на простые (однофакторные) и множественные (многофакторные). Однофакторной называется связь, если исследуется зависимость между одним признаком-фактором и результативным признаком. Такие связи называются также парными. Многофакторные связи – это связи между несколькими (двумя и более) факторными признаками и результативным признаком.

Связи между общественными явлениями, установленные на основе теоретического анализа, могут быть изучены, измерены и количественно выражены с помощью различных статистических методов.

Для исследования функциональных связей применяются балансовый и индексный методы. Для исследования корреляционных связей применяют метод сравнения параллельных рядов, метод аналитических группировок, графический метод, корреляционно-регрессионный анализ(КРА).

Измерить тесноту связи – это определить, насколько вариация результативного признака зависит от вариации факторного признака.

Для количественной характеристики тесноты связи между признаками используют следующие показатели: 1) эмпирический коэффициент детерминации, 2) эмпирическое корреляционное отношение, 3) теоретическое корреляционное отношение, 4) линейный коэффициент корреляции и др.

Для успешного усвоения темы 9 необходимо ознакомиться с представленным теоретическим материалом и целесообразно решить предлагаемые задачи.

Один из наиболее распространенных методов изучения связей – метод группировок в сочетании с методом средних. Этот метод позволяет установить наличие связи, определить направление связи, приближенно измерить тесноту связи.

Методика применения группировок в сочетании с методом средних при изучении связей заключается в следующем:

1) проводят группировку изучаемой совокупности по величине факторного признака;

2) рассчитывают среднее значение результативного признака для каждой группы;

3) сопоставляют направление изменения среднего значения результативного признака с направлением изменения факторного признака.

Рассматриваемый метод позволяет измерить тесноту связи. Для этого используют показатели вариации результативного признака: общую дисперсию (s²) и межгрупповую дисперсию (d²). Общая дисперсия показывает вариацию результативного признака, вызванную всеми действующими на нее факторами. Формулы для ее расчета приведены в теме 5 «Средние величины и показатели вариации». Межгрупповая дисперсия характеризует вариацию результативного признака, вызванную признаком-фактором, положенным в основание группировки:

d² = ,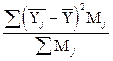

где – среднее значение результативного признака в j -й группе;

– число единиц в j -й группе.

Разделив межгрупповую дисперсию на общую, получим эмпирический коэффициент детерминации:

h_э² = .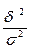

Его значения находятся в пределах: 0≤h_э²≤1.

Эмпирический коэффициент детерминации показывает, какая доля вариации результативного признака вызвана признаком, положенным в основание группировки. Чем больше эта доля, тем сильнее влияние факторного признака на результативный. Поэтому коэффициент детерминации используется как показатель тесноты связи между факторным и результативным признаком. При h_э²=0 связь между признаками отсутствует. При h_э²=1 связь функциональная, вся вариация вызвана группировочным признаком.

В качестве показателя тесноты связи используют также эмпирическое корреляционное отношение, представляющее собой квадратный корень из коэффициента детерминации:

h_э = .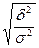

Его значения также находятся в пределах: 0≤h_э≤1.

Чем ближе корреляционное отношение к 0, тем связь слабее; чем ближе оно к 1, тем связь теснее.

Принято считать, что если h_э >0,5, то связь заметная, если h_э >0,7, – то высокая, если h_э >0,9, – то весьма высокая.

Когда установлено, что связь высокая, можно продолжать исследование зависимости признаков нахождением линии регрессии.

Другой показатель тесноты связи – линейный коэффициент корреляции (r) – служит показателем тесноты связи в случае линейной зависимости между признаками. Этот показатель рассчитывается по различным формулам в зависимости от исходных данных, например:

,

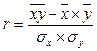где 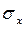и 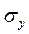– среднеквадратические отклонения факторного и результативного признаков.

Его значения находятся в пределах: –1 ≤ r ≤1.

Знак линейного коэффициента корреляции указывает направление связи (знак «+» свидетельствует о прямой связи, знак «–» – об обратной связи). Чем ближе коэффициент к 1, тем сильнее связь факторного и результативного признаков.

Рассмотрим типовую задачу исследования зависимости производительности труда от энерговооруженности труда.

Имеется следующая информация по 25 промышленным предприятиям региона:

№ п/п	Энерговооруженность труда, кВт.ч (Х)	Производительность труда, шт. (Y)
	7,1
	7,2
	7,9
	8,3
	8,5
	9,0
	9,3
	9,6
	9,7
	10,2
	10,5
	11,0
	11,6
	12,3
	12,4
	12,6
	12,8
	13,2
	13,4
	13,7
	13,8
	14,0
	14,1
	14,3
	14,4

Определите:

1) наличие и направление связи между производительностью труда и его энерговооруженностью;

2) тесноту связи между исходными признаками.

Сделайте выводы.

1. Установим наличие и направление зависимости производительности труда от энерговооруженности труда с помощью аналитической группировки изучаемой совокупности: 25 предприятий разобьем на 5 групп с равным интервалом по величине факторного признака (Х).

1.1. Находим размер интервала (i) следующим образом:

i=R/n,

где R – размах вариации, который определяется как разность между максимальным и минимальным значениями признака;

n – установленное число групп (определяется либо по формуле Стерджесса, либо устанавливается исследователем).

В нашем случае

i = =1,46»1,5(кВт.ч).

1.2. Далее установим полную шкалу интервалов по методологии, изложенной в теме «Сводка и группировка статистических материалов».

1.3. Подсчитаем число предприятий, входящих в каждую группу.

1.4. Рассчитаем средние уровни производительности труда в каждой группе и в целом по совокупности:

,

где – среднее значение результативного признака для каждой j -й группы;

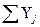– сумма значений результативного признака;

M_j – число предприятий в каждой группе.

Аналогичным образом по всей совокупности получим:

= =18,44(шт.).

1.5. Построим расчетно-аналитическую групповую таблицу:

Зависимость производительности труда от энерговооруженности:

Группы предприятий по энерговооруженности, кВт.ч (Х)	Число предприятий в группе (Мj)	Средняя производительность труда, шт. ()	( - )^2Мj
7,1-8,6 8,6-10,1 10,1-11,6 11,6-13,1 13,1-14,6		15,4 16,5 18,8 20,0 20,4	46,208 15,054 0,389 12,168 30,733
Итого		18,4	104,552

2. Оценим тесноту связи между изучаемыми признаками с помощью эмпирического корреляционного отношения (методика расчета которого рассмотрена выше):

h_э = .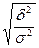

2.1. Предварительно рассчитываем общую дисперсию (s²), характеризующую вариацию результативного признака вследствие влияния всех действующих на него факторов:

σ² = = 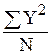- = -18,44²=345,720-340,034=5,684.

2.2. Рассчитаем межгрупповую дисперсию (d²) в соответствии с вышеизложенной методикой:

d² = = =4,18.

2.3. Произведенные расчеты позволяют определить эмпирическое корреляционное отношение:

h_э = = =0,857.

Полученные результаты свидетельствуют о том, что вариация результативного показателя (производительности труда) на 73,5% обусловлена влиянием энерговооруженности труда на предприятиях и соответственно на 26,5% – влиянием неучтенных факторов.

2.4. Определим коэффициент корреляции:

.

Связь между изучаемыми признаками высокая.

Дата добавления: 2014-11-20