Задачи для самостоятельной работы

Выборочное наблюдение (ВН) – один из видов несплошного наблюдения. Выборочным наблюдением называют такое несплошное наблюдение, при котором статистическому обследованию подвергаются не все единицы изучаемой совокупности, а лишь отобранные случайным образом.

Методические указания

Эта тема связана со многими другими темами курса теории статистики, а также с математической статистикой и теорией вероятностей, в которых дается математическая теория закона больших чисел, являющаяся теоретической основой выборочного метода исследования.

Вначале здесь необходимо выяснить причины применения выборочного наблюдения, далее надо ознакомиться с основными его понятиями. Один из вопросов темы – виды выборки (повторная и бесповторная) и способы отбора, обеспечивающие репрезентативность выборки (случайный или собственно случайный, механический, типический, серийный).

Главными вопросами этой темы являются определение средней ошибки выборки собственно случайного отбора – для средней и для доли; предельной ошибки выборки при заданном уровне вероятности; пределов для средней и для доли; необходимой численности выборки (объема выборки).

Для успешного усвоения темы 8 необходимо ознакомиться с представленным теоретическим материалом и целесообразно решить предлагаемые задачи.

Цель ВН состоит в том, чтобы по характеристикам отобранной части единиц судить о характеристиках всей совокупности.

Причины применения ВН:

1) экономия времени и средств в результате сокращения объема работ;

2) минимум порчи или даже уничтожения исследуемых объектов;

3) необходимость детального исследования каждой единицы наблюдения при невозможности охвата всех единиц;

4) достижение большей точности результатов обследования.

При изучении темы необходимо усвоить следующие понятия:

а) генеральная совокупность – вся изучаемая совокупность (общее число рабочих завода). Объем генеральной совокупности обозначают N;

б) выборочная совокупность – часть генеральной совокупности, отобранная для ВН. Число единиц выборочной совокупности обозначают n;

в) генеральная средняя (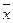) – средняя величина признака для генеральной совокупности;

г) выборочная средняя () – средняя величина признака для выборочной совокупности;

д) генеральная доля (p) – отношение числа единиц генеральной совокупности, обладающих значением изучаемого признака ко всему числу единиц генеральной совокупности;

е) выборочная доля (w) – отношение числа единиц выборочной совокупности, обладающих значением изучаемого признака к числу единиц выборочной совокупности, т.е. это доля признака в выборочной совокупности.

Различают повторную и бесповторную выборку. При повторной выборке единицы генеральной совокупности, попавшие в выборку, вновь возвращаются после обследования в генеральную совокупность и участвуют в дальнейшей процедуре отбора, а при бесповторной – не возвращаются.

Примером повторной выборки является обследование пассажиропотока на городском транспорте, а бесповторной – выборочное изучение качества какой-либо продукции. Бесповторная выборка применяется чаще, чем повторная.

Различают следующие основные способы отбора:

1) случайный (собственно случайный);

2) типический;

3) серийный (гнездовой);

4) механический.

Первые три способа отбора могут быть проведены с помощью повторной или бесповторной выборки, механический отбор производится только с помощью бесповторной выборки.

В процессе ВН возникают специфические ошибки – ошибки репрезентативности (ОР). Они возникают вследствие различия структуры выборочной и генеральной совокупностей. В общем виде ОР – это разность между обобщающими выборочными показателями и соответствующими показателями генеральной совокупности. ОР для средней – это 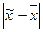, а для доли – .

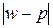Для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки.

Средняя ошибка выборки показывает, на сколько в среднем отклоняются выборочные характеристики от генеральных. Если обследуется признак в форме средней, то средняя ошибка выборки () определяется:

а) при повторной выборке:

,

где – выборочная дисперсия,

– объем выборки;

б) при бесповторной выборке:

,

где N – объем генеральной выборки,

– доля выборки.

Вторая формула может быть использована не только для собственно случайного отбора, но и для механического.

Если обследуется признак в форме доли, то средняя ошибка выборки () определяется:

а) при повторной выборке:

,

где w – доля признака в выборочной совокупности;

б) при бесповторной выборке:

.

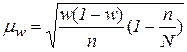Заметим, что формулы повторной и бесповторной выборки отличаются на выражение , которое всегда меньше единицы. Из этого следует, что средняя ошибка выборки при бесповторном отборе меньше средней ошибки выборки при повторном отборе.

При проведении выборочного наблюдения исследователя устраивает средняя ошибка выборки в определенных границах. Поэтому необходимо ориентироваться на предельную ошибку выборки при заданном уровне вероятности.

Предельная ошибка выборки () – это наперед заданное сколь угодно малое число, которое определяется по формуле:

,

где – коэффициент доверия, зависящий от вероятности, определяется по соответствующим таблицам (если, например, =0,954, то =2, если =0,997, то =3).

Таким образом, предельная ошибка выборки равна t -кратной средней ошибки. Для ее определения при заданном уровне вероятности необходимо: а) определить среднюю ошибку выборки () – по соответствующей формуле, б) исходя из заданной вероятности , с помощью специальных таблиц, найти число , соответствующее вероятности, в) найти произведение .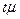

Пределы (вероятные границы, доверительные интервалы), в которых находятся соответствующие генеральные показатели, устанавливаются по следующим формулам:

1) для средней:

,

где 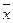– генеральная средняя;

– выборочная средняя;

– предельная ошибка выборочной средней;

2) для доли:

,

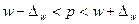где 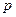– генеральная доля;

w – выборочная доля;

– предельная ошибка выборочной доли.

Определение объема выборки (n) при заданной ее точности является проблемой, обратной рассмотренной ранее – определение предельной ошибки выборки при данном ее объеме. Формула объема выборки – в четырех вариантах – получается из соответствующей формулы предельной ошибки.

Если обследуется признак в форме средней, то объем выборки при повторной выборке определяется:

;

при бесповторной выборке:

.

Если обследуется признак в форме доли, то объем выборки при повторной выборке определяется:

,

при бесповторной выборке:

.

Для успешного усвоения темы целесообразно решить предлагаемые типовые задачи.

Типовая задача 1

Для определения среднего срока пользования краткосрочным кредитом в банке была проведена пяти процентная бесповторная выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении – 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней.

С вероятностью 0,954 определите пределы, в которых будет находиться срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования более 60 дней.

Для определения пределов, в которых будет находиться срок пользования краткосрочным кредитом в генеральной совокупности, рассчитаем среднюю и предельную ошибки выборки. Так как отбор бесповторный и обследуется признак в форме средней, то воспользуемся следующими формулами:

- средняя ошибка выборки:

;

- предельная ошибка выборки:

.

Для вероятности 0,954 t =2. Следовательно, дней.

Тогда пределы, в которых будет находиться срок пользования краткосрочным кредитом в генеральной совокупности, определяются как:

,

,

.

Срок пользования краткосрочным кредитом находится в границах от 28,2 до 31,8 дней.

Определим долю счетов со сроком пользования более 60 дней.

Выборочная доля счетов со сроком пользования более 60 дней равна:

.

Средняя ошибка выборки для доли счетов со сроком пользования более 60 дней определяется по формуле:

,

.

Предельная ошибка выборки для доли счетов со сроком пользования более 60 дней равна:

.

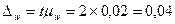Тогда пределы, в которых будет находиться доля счетов со сроком пользования более 60 дней, равны:

,

,

.

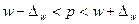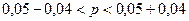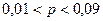Удельный вес счетов со сроком пользования более 60 дней находится в границах от 1 до 9%.

Типовая задача 2

Произведено выборочное обследование длительности производственного стажа рабочих. В выборку было взято 200 рабочих из общего количества в 1000 человек. Результаты выборки следующие:

Стаж, лет	2-4	4-6	6-8	8-10
Число рабочих

На основании приведенных данных определить:

1) с вероятностью 0,954 возможные пределы колебаний средней продолжительности стажа всех рабочих;

2) какое число рабочих надо взять в выборку, чтобы ошибка не превышала 0,5 года на основе приведенных выше показателей.

1. Возможные пределы колебания среднего стажа рабочих:

,

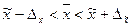где предельная ошибка определяется по формуле .

Определим средний стаж и дисперсию стажа работников и подставим полученные значения в формулу предельной ошибки выборки:

лет,

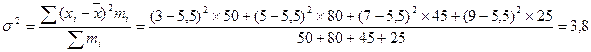
года.

,

.

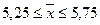Средний стаж рабочих предприятия с вероятностью 0,954 находится в границах от 5,25 до 5,75 года.

2. Объем выборки рассчитывается по следующей формуле:

рабочих.

Для выполнения поставленных условий необходимо обследовать 58 рабочих.

ЗАДАЧА 1

Произведено выборочное наблюдение для определения доли брака продукции. В выборке было взято 400 единиц изделий из общего количества в 4 тыс. единиц. В результате выборки обнаружен брак в 65 изделиях.

Определите:

1) размеры колебаний брака во всей партии с вероятностью 0,954;

2) сколько продукции должно быть выборочно обследовано для определения доли брака с ошибкой, не превышающей 1% исходя из приведенных выше показателей.

ЗАДАЧА 2

На ткацкой фабрике работает 800 ткачих. В порядке случайной повторной выборки определена средняя дневная выработка 100 ткачих. В итоге этого обследования получены следующие данные:

Дневная выработка, м	350-450	450-550	550-650
Число ткачих

Определите с вероятностью 0,997 пределы нахождения средней выработки всех ткачих фабрики.

ЗАДАЧА 3

Произведено выборочное наблюдение для определения доли брака продукции. В выборку было взято 900 единиц изделий из общего количества в 5 тыс. единиц. В результате выборки был обнаружен брак в 70 изделиях.

Определите:

1) численность бракованных единиц продукции во всей партии с вероятностью 0,954;

2) сколько продукции должно быть обследовано для определения доли брака с ошибкой, не превышающей 1%, исходя из приведенных выше показателей, с вероятностью 0,997.

ЗАДАЧА 4

При обработке материалов учета городского населения методом случайного бесповторного отбора было установлено, что в городе 10% жителей в возрасте свыше 60 лет. При этом из общей численности города (400 тыс. человек) выборкой было охвачено 100 тыс. человек.

Определите, с вероятностью 0,954 в каких пределах колеблется доля жителей в возрасте старше 60 лет среди всего населения города.

ЗАДАЧА 5

В городе проживает 10 тыс. семей. С помощью выборки предполагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2?

ЗАДАЧА 6

Для определения средней влажности 10 т пшеницы проводится случайная бесповторная выборка. Сколько проб весом 200 г необходимо взять для того, чтобы с вероятностью 0,997 гарантировать ошибку средней влажности всего зерна, не превышающую 0,1%? Среднее квадратическое отклонение по данным прошлого обследования равно 0,6%.

Дата добавления: 2014-11-20