Комбинаторика формулалары 10 страница

№17 25 нұсқа

1 Кездейсоқ шама 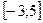кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 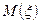математикалық күтімін, 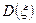дисперсиясын табу керек.

2 Кездейсоқ шама 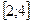кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 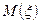математикалық күтімін, 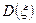дисперсиясын табу керек.

3 Кездейсоқ шама 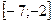кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 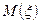математикалық күтімін, 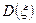дисперсиясын табу керек.

4 Кездейсоқ шама 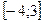кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 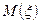математикалық күтімін, 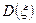дисперсиясын табу керек.

5 Кездейсоқ шама 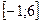кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 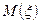математикалық күтімін, 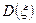дисперсиясын табу керек.

6 Кездейсоқ шама 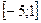кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 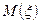математикалық күтімін, 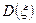дисперсиясын табу керек.

7 Кездейсоқ шама 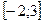кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 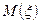математикалық күтімін, 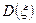дисперсиясын табу керек.

8 Кездейсоқ шама 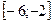кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 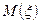математикалық күтімін, 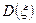дисперсиясын табу керек.

9 Кездейсоқ шама 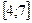кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 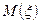математикалық күтімін, 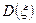дисперсиясын табу керек.

10 Кездейсоқ шама 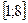кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 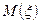математикалық күтімін, 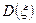дисперсиясын табу керек.

11 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 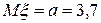, 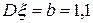.Үлестірім тығыздығын жазыңыз.

12 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 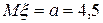, 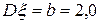.Үлестірім тығыздығын жазыңыз.

13 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 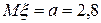, 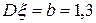.Үлестірім тығыздығын жазыңыз.

14 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 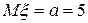, 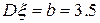.Үлестірім тығыздығын жазыңыз.

15 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 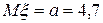, 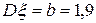.Үлестірім тығыздығын жазыңыз.

16 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 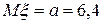, 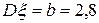.Үлестірім тығыздығын жазыңыз.

17 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 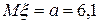, 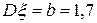.Үлестірім тығыздығын жазыңыз.

18 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 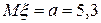, 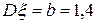.Үлестірім тығыздығын жазыңыз.

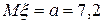19 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері , .Үлестірім тығыздығын жазыңыз.

20 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 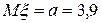, 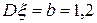.Үлестірім тығыздығын жазыңыз.

21 Кездейсоқ шама қалыпты үлестірім заңымен берілген. Параметрлері 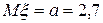, 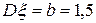.Үлестірім тығыздығын жазыңыз.

22 Кездейсоқ шама 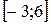кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 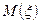математикалық күтімін, 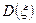дисперсиясын табу керек.

23 Кездейсоқ шама 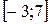кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 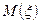математикалық күтімін, 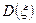дисперсиясын табу керек.

24 Кездейсоқ шама 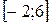кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 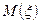математикалық күтімін, 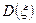дисперсиясын табу керек.

25 Кездейсоқ шама 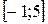кесіндісінде бірқалыпты үлестірім заңымен берілген. Кездейсоқ шаманың үлестірім тығыздығын, 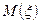математикалық күтімін, 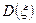дисперсиясын табу керек.

4 МАТЕМАТИКАЛЫҚ СТАТИСТИКА ЭЛЕМЕНТТЕРІ ТЕОРИЯСЫНАН ҚЫСҚАША МӘЛІМЕТТЕР

4.1 Математикалық статистика есептері

Математикалық статистиканың негізгі мақсаты тәжірибелік деректерді алу әдістерін жасау, нәтижелерді өңдеу және оны түсіндіру әдістерін әзірлеу, осы әдістерді қолдана отырып, кездейсоқ шамалардың үлестірілім заңдарын табу.

Математикалық статистиканың басты қарастыратын мәселелері: бақылау нәтижесінде алынған деректерді жинау әдістерін көрсету және оларды топтау.

Математикалық статистиканың тағы бір есебі- зерттеу мақсатына сәйкес статистикалық деректерді талдау әдістерін анықтау. Бұған:

а)оқиғаның белгісіз ықтималдығын бағалау; белгісіз үлестірілім функциясын бағалау; түрі белгілі үлестірілім параметрлерін бағалау; кездейсоқ шаманың бір немесе бірнеше кездейсоқ шамалардан тәуелділігін бағалау жатады;

б)белгісіз үлестіру түрі немесе түрі белгілі үлестіру параметрлерінің шамасы туралы статистикалық болжамдарды тексеру жатады.

Математикалық статистика математикалық зерттеу барысында керек сынақтар санын анықтау әдістерін әзірлейді(сынақтарды жоспарлау), зерттеу барысында ағымды талдау жүргізеді.

Сонымен математикалық статистиканың мақсаты ғылыми және тәжірибелік қорытындылар алу үшін статистикалық деректерді жинау және өңдеу әдістерін құру.

4.2 Бас және таңдамалы жиынтықтар

Біртекті объектілерді сапалық немесе сандық белгілері бойынша зерттеу керек болсын. Мысалы детальдар партиясы: сапалық белгісі детальдың стандартты болуы, сандық белгісі детальдың бақыланатын өлшемі.

Жалпылама зерттеу жүргізуге болады, бірақ тәжірибе жүзінде жалпылама, жаппай зерттеу жүргізу өте қиын, сондықтан жиынтықтан объектілердің санаулы түрін алып, зерттеуге тура келеді.

Кездейсоқ таңдалған объектілер жиынтығы таңдамалы жиынтық немесе таңдама деп аталады.

Таңдама алынған объектілер жиыны бас жиынтық деп аталады.

Жиынтықтағы объектілер саны жиынтық көлемі деп аталады.

Мысалы 1000 детальдан 100 деталь зерттеуге алынса, бас жиынтық көлемі N=1000, таңдама көлемі n=100.

Ескерту: Бас жиынтықта объктілер саны шектеулі немесе шексіз көп болуы мүмкін. Бұл жағдай сынақ нәтижесіне әсер етпейді.

4.3 Іріктеу әдістері

Тәжірибе жүзінде саналуан іріктеу әдістері қолданылады. Бұл әдістерді екі түрге бөлуге болады:

- Бас жиынтықты мүшелерге бөлшектеуді керек етпейтін іріктеу. Бұған:

- қарапайым кездейсоқ кайталанбайтын іріктеу;

- қарапайым кездейсоқ қайталанатын іріктеу

жатады.

- Бас жиынтықты бөлшектейтін іріктеу. Бұған:

- типтік іріктеу;

- механикалық іріктеу;

- сериялық іріктеу

жатады.

Бас жиынтықтан бір бірлеп іріктелетін іріктеу қарапайым кездейсоқ іріктеу деп аталады.

N көлемді бас жиынтықтан (карточкалар 1- ден N- ге дейін белгіленген) жақсылап араластырылғаннан кейін біреуі таңдап алынып, зерттеледі, содан кейін қайтарылып, келесі карточка алынып зерттеледі.

Егер карточка қайтарылмаса, кездейсоқ қайталанбайтын іріктеу деп аталады.

Егер бас жиынтық көлемі үлкен болса, іріктеуді орындау қиын болатыны көрініп тұр.

Егер объектілер бас жиынтықтан емес, әр типтік ауданнан таңдалса, іріктеу типтік деп аталады.

Мысалы бірнеше станок жасаған датальдарды жалпылама таңдамай, әр станоктың детальдарын жеке жеке таңдаса типтік іріктеу болады.

Егер бас жиынтық таңдамаға неше объект енсе, сонша топқа бөлінсе (әр топтан бір бір объект таңдалады), онда іріктеу механикалық іріктеу деп аталады.

Жаппай зерттеу жүргізілгенде объектілер бір бірлеп емес партиямен таңдалса, іріктеу сериялық деп аталады.

Іс жүзінде іріктеулер түрі араластырыла қолданылады.

4.4 Таңдаманың статистикалық үлестірілімі

X cандық белгіcін зерделеуге бас жинақтан n- көлемді 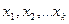таңдамасы алынсын.

X белгісінің бақыланатын 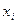мәндері варианталар деп, ал өсу ретімен жазылған варианталар тізбегі варияциялық қатар деп аталады.

Бақылау саны жиілік деп аталады, жиіліктің көлемге қатнасы

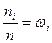
салыстырмалы жиілік деп аталады.

Варияциялық қатардың 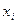варианталар тізбегі мен оларға сәйкес 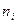жиіліктер тізбегі таңдаманың статистикалық үлестірілімі деп аталады.

Ықтималдықтар теориясында кездейсоқ шамалардың мүмкін қабылдайтын мәндері мен олардың ықтималдықтарының арасындағы сәйкестік үлестірілім деп аталады, математикалық статистикада бақыланатын варианталар мен олардың орындалу жиіліктерінің арасындағы сәйкестік үлестірілім деп аталады.

Мысал

Таңдама жиіліктерінің үлестірілімі берілген, көлемі 20.

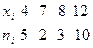
Салыстырмалы жиілік үлестірілімін табу керек.

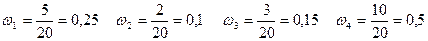
Ізделінген салыстырмалы жиілік үлестірілімін жазайық:

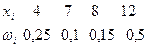
Тексеру: 0,25+0,1+0,15+0,5=1

4.5 Үлестірудің эмпирикалық функциясы

Әрбір x- тің мәні үшін 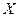< 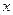оқиғасының салыстырмалы жиілігін анықтайтын

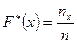
функциясы үлестірудің эмпирикалық функциясы деп аталады. 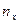- варианталар саны, n- таңдама көлемі.

Эмпирикалық функцияның келесі қасиеттері бар.

1- қасиет. Эмпирикалық функцияның мәндері 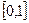кесіндісінде жатады.

2- қасиет. 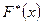- кемімейтін функция.

3- қасиет. Егер 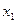- ең кіші варианта, ал 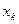- ең үлкен варианта болса, онда 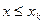болғанда 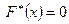болады, 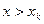болғанда 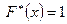болады.

4.6 Үлестіру параметрлерінің статистикалық бағалары

4.6.1 Нүктелік бағалар

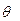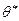Теориялық үлестірілімнің белгісіз параметрі - ның статистикалық бағасы деп бақыланатын 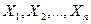кездейсоқ шамаларының 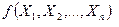функциясы аталады.

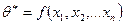санымен анықталатын статистикалық баға нүктелік деп аталады, бұл формуладағы - X сандық белгісін n- рет бақылаудың нәтижесі.

Математикалық үміті таңдаманың кез келген көлемінде бағаланатын параметрге тең болатын нүктелік баға ығыспайтын баға деп аталады.

Математикалық үміті таңдаманың кез келген көлемінде бағаланатын параметрге тең болмайтын нүктелік баға ығыспалы баға деп аталады.

Таңдамалы орта бас ортаның ығыспайтын бағасы болады:

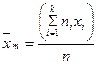
Таңдамалы дисперсия бас дисперсияның ығыспалы бағасы болады:

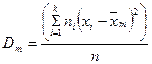
Есептеулерге келесі формула ыңғайлырақ болады:

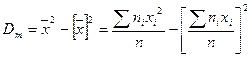
Бас дисперсияның ығыспайтын бағасы ретінде түзетілген таңдамалы дисперсия қабылданады:

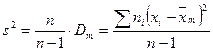
Есептеулерге келесі формула ыңғайлырақ болады:

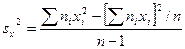
4.6.2 Аралық бағалар

Екі санмен- аралықтың шеткі нүктелерімен- анықталатын баға аралық баға деп аталады.

Белгісіз параметрді берілген 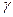- сенімділігімен анықтайтын аралық сенімділік аралығы деп аталады.

4.6.2.1 Нормальды үлестірілген X сандық белгісінің а математикалық үмітінің 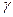- сенімділігімен алынған (бас жиынтықтың белгілі 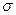орта квадрат ауытқуы бар болатын) аралық бағасы ретінде

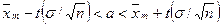
сенімділік аралығы қабылданады. Бұл формуладағы 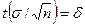- баға дәлдігі, n- таңдама көлемі, t- 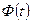Лаплас функциясы аргументінің мәні, және 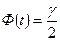болады және Б қосымшасынан табылады;

Егер бас жиынтықтың 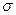орта квадрат ауытқуы белгісіз болса, аралық баға болатын сенімділік аралығы келесі түрде қабылданады:

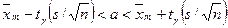
бұл формуладағы s- «түзетілген» таңдамалы орта квадрат ауытқу, 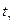- берілген n мен 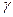бойынша В қосымшасынан табылады.

4.6.2.2 Нормальды үлестірілген X сандық белгісінің 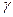- сенімділігімен алынған 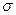орта квадрат ауытқуының «түзетілген» таңдамалы орта квадрат ауытқуы S бойынша аралық бағасы

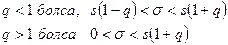
сенімділік аралығы болады. q- берілген n мен 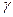бойынша Г қосымшасынан табылады.

4.6.2.3 Биномдық үлестірілімдегі белгісіз ықтималдығы р-ның (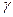 - сенімділігімен) w салыстырмалы жиілігі бойынша аралық бағасы ретінде

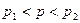
сенімділік аралығы қабылданады. Бұл формуладағы:

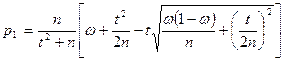
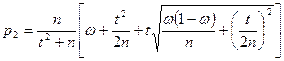
n- сынақтардың жалпы саны, m- оқиғаның орындалу саны, 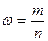- салыстырмалы жиілік, t- 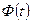Лаплас функциясы аргументінің мәні, және 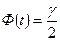болады(Б қосымшасы), 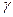- берілген сенімділік.

4.7 Таңдаманың келтірімділік сипаттамаларын есептеу әдістері

4.7.1 Таңдамалы орта мен дисперсияны есептеудің көбейту әдісі

4.7.1.1 Бірдей аралықты варианталар.

Таңдама бірдей аралықты варианталар мен олардың сәйкес жиіліктерінің үлестірілімі түрінде берілсін. Бұл жағдайда таңдамалы орта мен таңдамалы дисперсияны көбейту әдісімен табуды келесі формулалармен орындау қолайлы болады:

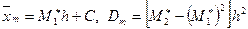
h- көршілес варианталардың айырмасы, қадам; С- жалған ноль, вариациялық қатардың мөлшермен ортасында орналасқан варианта;

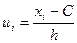
шартты варианта;

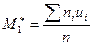
бірінші ретті шартты момент;

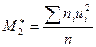
екінші ретті шартты момент.

4.7.1.2 Әртүрлі аралықты варианталар.

Егер алғашқы варианталар бірдей аралықты болмаса, онда таңдаманың түгел варианталары орналасқан аралықты ұзындығы h болатын бірдей бірнеше дербес аралықтарға бөлеміз(әрбір жекеше аралық кем дегенде 8-10 вариантадан құралады). Содан кейін жекеше аралықтардың ортасы табылады, осы орталар тізбектелген бірдей аралықты варианталарды құрайтын болады. Әрбір аралық ортасының жиілігі ретінде, жекеше интервалға енетін варианталар жиіліктерінің қосындысы алынады.

Дата добавления: 2014-11-08