Комбинаторика формулалары 11 страница

Таңдамалы дисперсия есептегенде, топтау нәтижесіндегі қателікті азайту үшін Шеппард түзетуін енгізеді, басқаша айтқанда есептелген дисперсиядан жекеше аралық ұзындығы квадратының 1/12 бөлігі алып тасталынады.

Сөйтіп, Шеппард түзетуін ескерумен дисперсия келесі формуламен есептеледі:

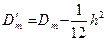
4.7.2 Эмпирикалық үлестірілімнің ассиметриясы мен эксцессі.

Ассиметрия мен эксцесс келесі теңдіктермен анықталады:

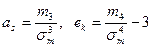
Бұл формуладағы 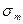- таңдамалы орта квадрат ауытқу; 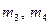- 3- және 4- ретті орталық эмпирикалық моменттер:

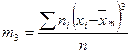
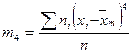
Бұл моменттерді h қадамды бірдей аралықты варианталар үшін келесі формулалармен есептеу тиімді:

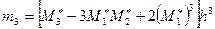
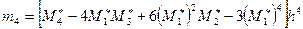
бұл формуладағы

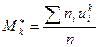
-к ретті шартты моменттер,

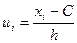
-шартты варианта. 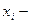алғашқы варианта, С- жалған ноль, басқаша айтқанда ең үлкен жиілікті варианта, мөлшермен вариациялық қатардың ортасында орналасады.

4.8 Корреляция теориясының элеметтері

4.8.1 Сызықты корреляция

Көп есептерде зерделенген кездейсоқ шаманың бір немесе бірнеше шамалардан тәуелділігін анықтау керек болады. Екі кездейсоқ шама функционалдық немесе статистикалық тәуелділікте болуы мүмкін. Әруақытта қатаң функционалдық тәуелділік бола бермейді, кездейсоқ шарттар әсер ету нәтижесінде статистикалық тәуелділік орындалады.

Егер бір шаманың өзгеруі екінші шаманың үлестірілімін өзгертсе, онда тәуелділік статистикалық тәуелділік деп аталады.

Дербес жағдай: Бір шаманың өзгеруі екіншісінің орта мәнін өзгертсе, онда статистикалық тәуелділік корреляциялық деп аталады.

Мысал

Y- бидай өнімі, X- тыңайтқаштар саны болсын. Бірдей өлшемді жер участогынан, бірдей тыңайтқыш салынса да, әртүрлі түсім түседі. (Ауа райы әсер ету нәтижесінде). Басқаша айтқанда, Y X- ке тәуелді емес, бірақ орта түсім тыңайтқыштар санынан тәуелді функция болады, сөйтіп Y X- пен корреляциялық тәелділікте.

Шартты математикалық үмітті бағалауға бақылау деректерімен табылатын орта шарттылар алынады.

X=x –ке сәйкес алынатын бақыланатын Y мәндерінің арифметикалық ортасы - шартты орта деп аталады.

Y –тің X- ке, X- тің Y- ке регрессия теңдеулері:

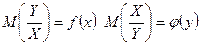
болады.

Шартты математикалық үміт x- тен тәуелді функция, ендеше оның бағасы шартты орта - те x- тен тәуелді болады.

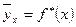
Бұл теңдеу Y –тің X- ке регрессиясының таңдамалы теңдеуі деп аталады; 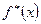- Y –тің X- ке таңдамалы регрессиясы деп, ал оның графигі Y –тің X- ке таңдамалы регрессия сызығы деп аталады.

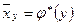
теңдеуі X- тің Y- ке регрессиясының таңдамалы теңдеуі деп аталады; 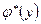- X- тің Y- ке таңдамалы регрессиясы деп, ал оның графигі X- тің Y- ке таңдамалы регрессия сызығы деп аталады.

Егер Y –тің X- ке және X- тің Y- ке регрессия сызықтары түзу болса, онда корреляция сызықты деп аталады.

Y –тің X- ке түзу сызықты регрессиясының теңдеуі

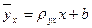
болады.

Бұл формуладағы:

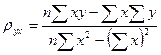
- Y –тің X- ке түзу сызықты регрессиясының таңдамалы коэффициенті болады.

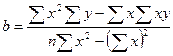
X- тің Y- ке түзу сызықты регрессиясының теңдеуі:

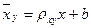
Алайда, бұл теңдеулерді басқа түрде қолданған тиімдірек болады. Сөйтіп, Y –тің X- ке түзу сызықты регрессияның таңдамалы теңдеуінің түрі келесі болады:

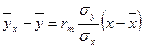
Бұл формуладағы - жоғарыда айтылғандай шартты орта, 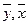X және Y белгілерінің таңдамалы орталары, 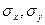- орта квадрат ауытқу орталары, 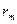- корреляцияның таңдамалы коэффициенті және ол келесі түрде табылады:

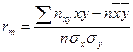
X –тің Y- ке түзу сызықты регрессияның таңдамалы теңдеуінің түрі келесі болады:

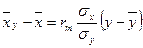
Егер X және Y белгілерін бақылау нәтижелері бірдей аралықты варианталары бар корреляциялық кесте түрінде берілсе, онда шартты варианталарға көшу тиімді болады:

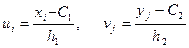
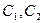- X және Y белгілері варианталарының жалған нольдері, жалған ноль ретінде мөлшермен вариациялық қатардың ортасында орналасқан және ең үлкен жиілікті вариантаны таңдаған тиімді, 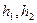- қадамдар, басқаша айтқанда X және Y белгілерінің көршілес орналасқан варианталарының айырмасы.

Бұл жағдайда корреляцияның таңдамалы коэффициенті

формуласымен есептеледі.

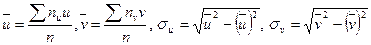
Бұл шамаларды білу нәтижесінде, регрессия теңдеуіне енетін шамаларды анықтауға болады:

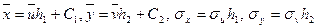
Сызықты корреляция байланысын бағалауға корреляциялық таңдамалы коэффициент қолданылады.

4.8.2 Қисық сызықты корреляция

Егер регрессия графигі қисықсызық болса, онда корреляция қисықсызықты деп аталады. 2- ші ретті параболалық корреляция болғанда, Y –тің X- ке регрессиясының таңдамалы теңдеуі келесі болады:

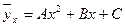
Белгісіз А, В, С параметрлері

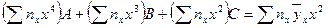
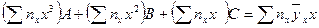
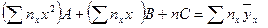
теңдеулер жүйесінен табылады.

X- тің Y- ке регрессиясының таңдамалы теңдеуі де осылайша табылады:

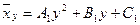
Y –тің X- ке корреляциялық күшін бағалауға таңдамалы корреляциялық қатынас қолданылады:

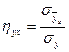
Бұл формуладағы

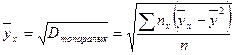
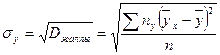
n- таңдама көлемі; 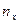- X белгісінің x мәнінің жиілігі; 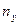- Y белгісінің y мәнінің жиілігі; - Y белгісінің шартты ортасы, 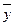- Y белгісінің жалпы ортасы.

X- тің Y- ке таңдамалы корреляциялық қатынасы да осылайша анықталады:

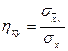
4.8.3 Рангтік корреляция

4.8.3.1Спирменнің рангтік корреляциясының таңдамалы коэффициенті.

n көлемді таңдаманың А және В сапалы белгілері бар тәуелсіз объектілері болсын. Сапалы белгіні дәл өлшеуге болмайды, бірақ ол объектілерді салыстыруға мүмкіндік береді, сөйтіп объектілерді сапасының кему немесе өсу ретімен орналастыруға болады. Объектілерді сапасының төмендеу ретімен орнастыруға шарттасайық.

Алдымен объектілерді А белгісімен сапасы төмендеу ретімен орналастырайық. I- орнында орналасқан объектке 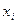рангін жазайық, ол сан объекттің орналасу ретіне сай: 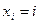. Ары қарай объекттерді В белгісімен сапасы төмендеу ретімен орналастырайық, және әрқайсысына 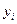рангін жазайық, және де рангтерді салыстыру ыңғайлы болу үшін y- тегі 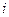индексі басындағыдай объекттің А белгісіндегі тізімдік номері болсын.

Сөйтіп, рангтердің 2 тізбегін аламыз:

А белгісімен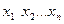

В белгісімен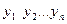

А және В белгілерінің байланыс дәрежесін бағалауға Спирмен мен Кендалдың рангтік корреляция коэффициенттері қолданылады.

Спирменнің рангтік корреляциясының таңдамалы коэффициенті

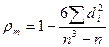
формуласымен табылады. 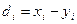, n- таңдама көлемі.

Спирменнің рангтік корреляция коэффициентінің абсолюттік шамасы 1- ден аспайды:

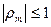
Сапалық белгілердің арасындағы байланысты негіздеу үшін Спирменнің рангтік корреляциясы таңдамалы коэффициентінің қомақтылығын тексеру керек.

4.8.3.2 Кендалдың рангтік корреляциясының таңдамалы коэффициенті.

Екі сапалы белгінің арасындағы байланысты Кендалдың рангтік корреляциясы коэффициентімен де бағалауға болады. N көлемді таңдама объектілерінің рангі келесі болсын:

А белгісімен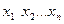

В белгісімен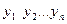

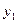- дің оң жағында одан үлкен болатын 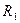ранг болсын, 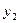- дің оң жағында одан үлкен болатын 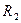ранг, 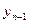- дің оң жағында одан үлкен болатын 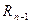ранг болсын. Рангтердің қосындысын белгілейік:

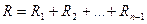
Кендалдың рангтік корреляциясының таңдамалы коэффициенті

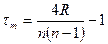
формуласымен табылады. N- таңдама көлемі, R- рангтер қосындысы.

Кендалдың рангтік корреляция коэффициентінің абсолюттік шамасы да 1- ден аспайды:

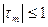
Сапалық белгілердің арасындағы байланысты негіздеу үшін Кендалдың рангтік корреляциясы таңдамалы коэффициентінің қомақтылығын тексеру керек.

4.9 Статистикалық гипотезаларды статистикалық тексеру

4.9.1 Негізгі түсініктер

Белгісіз үлестірілім немесе белгілі үлестірілім параметрлері туралы гипотеза статистикалық деп аталады.

Ұсынылған гипотеза нольдік(негізгі) гипотеза деп аталады.

Сыбайлас(альтернативті) гипотеза деп негізгі гипотезаға қарсы гипотеза аталады.

Бір немесе бірнеше болжамдары болатын гипотезалар болады.

Бір болжамды гипотеза қарапайым деп аталады.

Шектеулі немесе шектеусіз санды қарапайым гипотезалардан тұратын гипотеза күрделі деп аталады.

Гипотезаны тексеруді қорытындылау нәтижесінде екі текті қателер жіберілуі мүмкін.

1- текті қателік дұрыс болжамның жоққа шығарылуы. 1- ші текті қателіктің ықтималдығы қомақтылық деңгейі деп аталады және 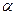деп белгіленеді.

2- текті қателік жалған болжамның қабылдануы. 2- ші текті қателіктің ықтималдығы деп белгіленеді.

Гипотезаны тексеретін К кездейсоқ шамасы статистикалық критерий деп аталады.

Таңдама нәтижесінде есептелген критерийдің мәні бақыланатын(эмпирикалық) мән деп аталады.

Нольдік(негізгі) гипотезаны жоққа шығаратын критерийдің мәндер жиыны кризистік облыс деп аталады.

Критерийдің нольдік(негізгі) гипотезаны қабылдайтын мәндер жиыны гипотезаның қабылдау облысы (жарамды облысы) деп аталады.

Статистикалық гипотезаларды тексерудің негізгі принципі келесі болады:

-егер критерийдің бақыланатын мәндері кризистік облыста жатса, онда нольдік гипотеза қабылданбайды;

-егер критерийдің бақыланатын мәндері қабылдау облысында жатса, онда гипотеза қабылданады.

Кризистік облысты гипотезаның қабылдау облысынан бөліп тұрған нүктелер 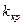кризистік нүктелер деп аталады.

Критерийдің қуаты деп конкурентті гипотеза әділ болғанда, критерийдің кризистік облысқа түсу ықтималдығын атаймыз. Басқаша айтқанда, критерийдің қуаты дегеніміз: конкурентті гипотеза әділ болғанда, нольдік гипотеза қабылданбау ықтималдығы.

4.9.2 Нормальдық бас жиынтықтардың дисперсияларын салыстыру

Бас жиынтықтан таңдап алынған, көлемдері 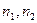болатын тәуелсіз таңдамалардан түзетілген таңдамалы дисперсиялар 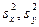табылған. Дисперсияларды салыстыру керек.

1-ереже. Берілген мәнділік деңгейі 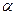бойынша 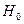нольдік гипотезасын тексеру үшін: (нольдік гипотеза- 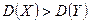деген 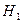конкуренттік гипотезасында 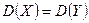деген тұжырым) критерийдің бақыланатын мәнін есептеу керек

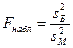
және Фишер- Снедекор кестесі бойынша, берілген мәнділік деңгейі 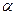мен бостандық дәрежелерін анықтайтын 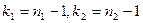сандары бойынша, 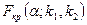кризистік нүктесін табу керек:

-егер 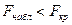болса, онда нольдік гипозаны қабылдау керек;

-егер 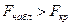болса, нолдік гипотезаны қабылдамау керек.

2- ереже. Егер конкуренттік гипотеза 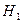: 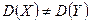болса, онда кризистік нүкте жартылай мәнділік деңгей 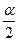мен бостандық дәрежелерін анықтайтын 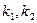сандары бойынша ізделінеді:

-егер 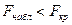болса, онда нольдік гипозаны қабылдау керек;

-егер 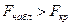болса, нолдік гипотезаны қабылдамау керек.

4.9.3 Нормальдық жиынтықтың түзетілген таңдамалы дисперсиясын жорамал бас дисперсиямен салыстыру.

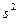түзетілген дисперсиясы табылған таңдама көлемі 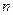деп деп белгіленді.

1- ереже. Берілген мәнділік деңгейі 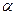бойынша 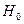нольдік гипотезасын тексеру үшін: (нольдік гипотеза- 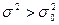деген 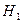конкуренттік гипотезасында белгісіз бас дисперсияның жорамал дисперсияға тең, басқаша айтқанда 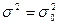деген тұжырым) критерийдің бақыланатын мәнін есептеу керек

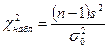
және 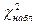үлестірілімі кестесі бойынша, берілген мәнділік деңгейі 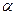мен бостандық дәрежелерін анықтайтын саны бойынша, 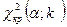кризистік нүктесін табу керек:

-егер 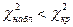болса, онда нольдік гипозаны қабылдау керек;

-егер 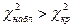болса, нольдік гипотезаны қабылдамау керек.

2- ереже. Егер конкуренттік гипотеза 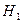: 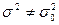болса, онда сол жақ кризистік нүкте 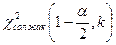мен оң жақ кризистік нүкте 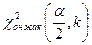-ты табу керек:

-егер болса, онда нольдік гипозаны қабылдау керек;

-егер 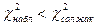т немесе болса, нолдік гипотезаны қабылдамау керек.

3- ереже. Егер конкуренттік гипотеза 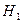: 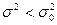болса, онда 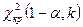кризистік нүктесін табу керек.

-егер 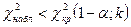болса, онда нольдік гипозаны қабылдау керек;

-егер 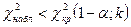болса, нольдік гипотезаны қабылдамау керек.

4.9.4 Дисперсиялары белгілі бас жиынтықтардың орталарын салыстыру.

1- ереже. Көлемдері үлкен болатын тәуелсіз таңдамалардың көлемдері n және m 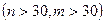деп белгіленген. Олардың сәйкес таңдамалы орталары табылған. Бас дисперсиялары D(X), D(Y) белгілі.

Берілген мәнділік деңгейінде 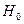нольдік гипотезасын тексеру үшін: (нольдік гипотеза- 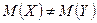деген 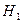конкуренттік гипотезасында дисперсиялары белгілі екі бас жиынтықтардың математикалық үміттерінің теңдігі туралы тұжырым, б.а. 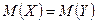) критерийдің бақыланатын мәнін есептеу керек

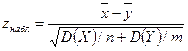
және Лаплас функцияларының Б қосымшасындағы кестесі бойынша

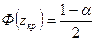
теңдігінен 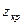кризистік нүктесін табу керек:

-егер 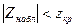болса, онда нольдік гипозаны қабылдау керек;

-егер 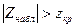болса, нольдік гипотезаны қабылдамау керек.

берілген мәнділік деңгейі 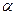мен бостандық дәрежелерін анықтайтын саны бойынша, 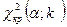кризистік нүктесін табу керек:

2- ереже. Егер конкуренттік гипотеза 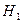: 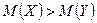болса, онда 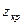кризистік нүктесі Лаплас функцияларының Б қосымшасындағы кестесі бойынша

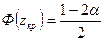
теңдігінен табылады:

-егер 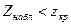болса, онда нольдік гипозаны қабылдау керек;

-егер 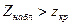болса, нольдік гипотезаны қабылдамау керек.

3- ереже. Егер конкуренттік гипотеза 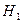: 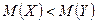болса, онда 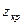«көмекші нүктесін» 2- ережемен табу керек:

-егер 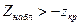болса, онда нольдік гипотезаны қабылдау керек;

-егер 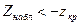болса, нольдік гипотезаны қабылдамау керек.

4.9.5 Дисперсиялары белгісіз және бірдей болатын (шамалы тәуелсіз таңдамалар) бас жиынтықтардың нормальдық орталарын салыстыру.

Шамалы тәуелсіз таңдамалардың көлемдері n және m 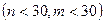деп белгіленген. Олардың сәйкес таңдамалы орталары және түзетілген таңдамалы дисперсиялары 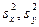табылған. Бас дисперсиялары белгісіз болса да, алдын ала бірдей екендігі белгілі.

Берілген 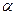мәнділік деңгейінде 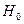нольдік гипотезасын тексеру үшін: (нольдік гипотеза- 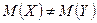деген 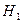конкуренттік гипотезасында дисперсиялары белгісіз, бірақ бірдей болатын екі нормальдық жиынтықтардың математикалық үміттерінің теңдігі туралы тұжырым, б.а. 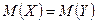) критерийдің бақыланатын мәнін есептеу керек

Дата добавления: 2014-11-08