Комбинаторика формулалары 1 страница

ОЖ 519.2

Жаксыгунова Ж.Т. Ықтималдықтар теориясы: мен математикалық статистика. 050729 «Құрылыс», 050730 «Құрылыс материалдарын, бұйымдары мен конструкцияларын өндіру», 050732 «Стандарттау, метрология және сертификаттау», 050718 «Электроэнергетика» 050716 «Аспаптар жасау» мамандықтарында мемлекеттік тілде күндіз оқитын студенттерге типтік есептерді орындауға арналған әдістемелік нұсқаулар, типтік есептер тапсырмалары. ШҚМТУ. Өскемен, 2009- 104 бет

Әдістемелік нұсқауда оқулықтармен жұмыс істеуге жалпы нұсқаулар бар, сонымен қатар, ықтималдықтар теориясы және математикалық статистика курсын өз еркімен меңгеруге көмектесетін теориялық мәліметтер, типтік есептеу тапсырмаларын орындау үлгілері, типтік есептер тапсырмалары бар.

Ақпараттық технологиялар және энергетика факультетінің әдістемелік кеңесінде құпталды.

Хаттама № 115 «18» __05__2009ж.

ã Д.Серікбаев атындағы

Шығыс Қазақстан

мемлекеттік техникалық

университеті, 2009

Әдістемелік нұсқаулар жоғары математика кафедрасында мемлекеттік білім стандарты, типтік оқу бағдарламасы негізінде 050729 «Құрылыс», 050730 «Құрылыс материалдарын, бұйымдары мен конструкцияларын өндіру», 050732 «Стандарттау, метрология және сертификаттау», 050718 «Электроэнергетика» 050716 «Аспаптар жасау» мамандықтарында мемлекеттік тілде күндіз оқитын студенттерге арналып жасалған.

Әдістемелік нұсқаулар Жоғары математика кафедрасының отырысында талқыланды.

Кафедра меңгерушісі Н.Ғ.Хисамиев

Хаттама № 8 «02» __04__2009 ж

Ақпараттық технологиялар және энергетика факультетінің әдістемелік кеңесінде құпталды.

Әдістемелік кеңес төрағасы А.П.Парамзин

Хаттама № 115 «_18» 05_2009 ж

Құрастырған Ж.Т. Жаксыгунова

Норма бақылаушысы Е.В. Петрова

МАЗМҰНЫ

Кіріспе 4

1 «Ықтималдықтар теориясынан» қысқаша мәліметтер 5

1.1 Ықтималдықтың классикалық анықтамасы

1.2 Комбинаторика формулалары 6

1.3 Геометриялық ықтималдық 7

1.4 Ықтималдықтардың қосу және көбейту теоремалары 7

1.5 Толық ықтималдық формуласы және Бейес формуласы 8

1.6 Сынақтар қайталануы. (Бернулли, Муавр - Лаплас,

Пуассон формулалары) 9

1.7 Кездейсоқ шамалар 10

1.8 Кездейсоқ шамалардың сандық сипаттамалары 12

2 Есептеу тапсырмаларын орындау үлгісі 13

2.1 Геометриялық ықтималдық 13

2.2 Ықтималдықтардың қосу және көбейту теоремалары 14

2.3 Толық ықтималдық формуласы және Бейес формуласы 16

2.4 Сынақтар қайталануы. (Бернулли, Муавр - Лаплас,

Пуассон формулалары) 17

2.5 Кездейсоқ шамалар 19

2.6 Кездейсоқ шамалардың сандық сипаттамалары 20

3 «Ықтималдықтар теориясынан» жеке орындау тапсырмалары 22

3. 1 Кездейсоқ оқиғалар. Ықтималдықтың классикалық анықтамасы. Комбинаторика формулалары

3.2 Геометриялық ықтималдық 31

3.3 Ықтималдықтарды қосу және көбейту теоремалары 33

3.4 Толық ықтималдық формуласы. Бейес формуласы 40

3.5 Сынақтар қайталануы. (Бернулли, Муавр - Лаплас,

Пуассон формулалары) 46

3.6 Кездейсоқ шамалар 49

4 Математикалық статистика элементтері теориясынан

қысқаша мәліметтер 70

4.1 Математикалық статистика есептері 70

4.2 Бас және таңдамалы жиынтықтар 70

4.3 Іріктеу әдістері 71

4.4 Таңдаманың статистикалық үлестірілімі 71

4.5 Үлестірудің эмпирикалық функциясы 72

4.6 Үлестіру параметрлерінің статистикалық бағалары 72

4.7 Таңдаманың келтірімділік сипаттамаларын есептеу әдістер 74

4.8 Корреляция теориясының элеметтері 75

4.9 Статистикалық гипотезаларды статистикалық тексеру 79

5 Есептеу тапсырмаларын орындау үлгісі 85

6 Жеке орындау тапсырмалары 93

ӘДЕБИЕТТЕР 97

А қосымшасы А.1 кесте- Жеке орындау тапсырмаларының берілген

мәндері 98

Ә қосымшасы Ә.1 кестесі- 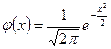функциясының мәндер кестесі 99

Б қосымшасы Б.1 кестесі- 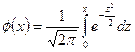функциясының мәндер

кестесі 101

В қосымшасы В.1 кестесі- 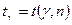мәндер кестесі 103

Г қосымшасы Г.1 кестесі- 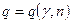мәндер кестесі 104

КІРІСПЕ

Ұсынылған әдістемелік нұсқаулар «Ықтималдықтар теориясы мен математикалық статистика» тарауларын игеруге көмектесу мақсатымен дайындалған.

Аталған тарауды меңгеру үшін студенттерге теориялық шолу, кездейсоқ оқиғалар, сынақтар қайталануы, кездейсоқ шамалар, таңдаманың статистикалық үлестірілуі, үлестіру параметрлерінің статистикалық бағалары, корреляция теориясының элементтері, статистикалық гипотезаларды статистикалық тексеру тақырыптарынан түсініктемелер келтірілген. Әрбір тақырыпқа есептер шығарылып, көрсетілген, сонымен қатар әрбір студентке жеке орындау тапсырмалары берілген. 25 нұсқау. Нұсқаудың номері студенттің тізімдегі номеріне сәйкес келеді.

Теориялық мәліметтер келтірілген, теориялық сұрақтар лекция мен көрсетілген оқулықтар бойынша игерілуі қажет.

Жеке орындау тапсырмаларын студент А-4 беттерге жазып, тапсырады.

Ықтималдықтар теориясы мен математикалық статистика жалпылама құбылыстардың ортақ заңдылықтарын зерттеу, әр құбылыстың нәтижесіне кездейсоқ факторлардың әсер етуін шама жағынан бағалайтын әдістерді жасау және белгісіз шарттарға сәйкес шешімдер қабылдау туралы ғылымдар.

Техникалық оқу орнындағы ықтималдықтар теориясы мен математикалық статистика курсы кездейсоқ оқиғалар: ықтималдықтар анықтамасы, негізгі теоремалар, сынақтар қайталануы; кездейсоқ шамалар: дискретті кездейсоқ шамалар, үздіксіз кездейсоқ шамалар; таңдамалы әдіс, үлестіру параметрлерін статистикалық бағалау, таңдаманың характеристика жинағын есептеу әдістері бөлімдерінен тұрады.

1 «ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫНАН» ҚЫСҚАША МӘЛІМЕТТЕР

1.1 Ықтималдықтың классикалық анықтамасы

Ықтималдықтар теориясының негізгі ұғымдарының бірі-оқиға. Егер белгілі бір шарттар жиынтығы орындалғанда болатын немесе болмайтын оқиға кездейсоқ деп аталады. Оқиға сынақ нәтижесі деп қарастырылады.

Анықтама. Оқиға ықтималдығы деп осы оқиға орындалуына қолайлы элементар жағдайлар санының осы сынақтағы барлық толық топ құрайтын бірдей мүмкіндікті, тең мүмкіндікті үйлесімсіз жағдайлар санына қатынасын айтамыз:

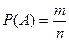
мұндағы n-барлық сынақтардың жалпы саны, m - А оқиғасы орындалатын сынақтар саны.

Ақиқат оқиға ықтималдығы p=1. Анықтамаға сүйенсек, А – ақиқат оқиға болғандықтан m=n болады да

P(A)=1.

Жалған оқиғаның ықтималдығы p=0. Бұл жағдайда анықтамаға сүйенсек, m=0 болады да

Кездейсоқ оқиға ықтималдығы 0 мен 1- дің аралығында анықталады:

0<P(A)<1

Сонымен, кез келген оқиғаның орындалу ықтималдығы 0≤P(A)≤1 теңсіздігін қанағаттандырады.

А және В оқиғаларының қосындысыдеп А оқиғасының орындалуын, немесе В оқиғасының орындалуын, немесе А және В оқиғаларының екеуініңде орындалуын айтамыз және былай белгілейміз А+В.

А және В оқиғаларының көбейтіндісідеп А мен В оқиғалары бірлесе орындалатын А·В оқиғасын айтамыз.

Егер А оқиғасының орындалуы В оқиғасының да орындалуын қамтамасыз етсе, онда А оқиғасы В оқиғасының құрамында жатады деп айтамыз, және былай белгілейміз АÌВ.

Егер АÌВ болса, онда А·В=А және А+В=В екендігі жоғарыдағы анықтамалардан шығады.

А және В оқиғаларының айырмасы деп А оқиғасы орындалып, В оқиғасы орындалмайтын оқиғаны айтамыз және С=A\B немесе C=A-B деп белгілейміз.

Сынақ нәтижесінде орындалған А оқиғасы В оқиғасының да орындалуын қамтыса (яғни, АÌВ) немесе осы сынақта В оқиғасының орындалуы А оқиғасының да орындалуын қамтыса (яғни ВÌА), онда А және В оқиғалары балама (эквивалент) деп аталады және А=B деп белгіленеді. Өзара балама оқиғалар теңбе-тең немесе тең оқиғалар деп аталады.

Белгілі бір шарттар жиыны іске асырылғанда, міндетті түрде орындалатын оқиға ақиқат оқиға деп аталады

Белгілі бір шарттар жиыны іске асырылғанда, алдын ала орындалмайтыны белгілі оқиға жалған оқиға деп аталады

Ақиқат оқиғаны U деп, жалған оқиғаны V деп белгілейміз.

Егер бір сынақта бір оқиғаның орындалуы басқа оқиғалардың орындалуын жоққа шығарса, онда оқиғалар үйлесімсіз деп аталады.

Егер А және В оқиғалары үйлесімсіз болса, онда А·В=V.

Қарама қарсы оқиғалар деп, толық топ құрайтын жалғыз мүмкіндікті екі оқиғаны айтамыз. Біреуі А оқиғасы деп, екіншісі 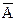деп белгіленеді.

Ендеше, осы анықтамаларға сүйене отырып, төмендегі теңдіктерге оңай көз жеткізуге болады:

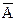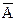А+А=А А·А=А А+ =U A· =V

A+V=A A·V=V A+U=U A·U=A

Оқиғалардың қосындысы, көбейтіндісі және айырмасының анықтамаларын қолдана отрып,мына төмендегі теңдіктерге көз жеткізуге болады:

АÈА=А АÇА=А АÈВ=ВÈА

АÇВ=ВÇА АÈ(ВÈС)=(АÈВ)ÈС АÇ(ВÇС)=(АÇВ)ÇС

А\В=АÇ 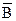АÇ(ВÈС)=АÇВÈАÇС (АÈВ)Ç(АÈС)=АÈВÇС

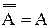
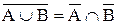
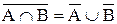
Шешуі «нешеу», «неше тәсілмен» деген сұрақтарды қажет ететін есептер комбинаторикалық есептерделінеді. Мұндай есептерді шешумен айналысатын математика саласы комбинаториканемесекомбинаторикалық математика деп аталады.

1- анықтама. Берілген әртүрлі n элементтен m элемент бойынша орналастырулар деп әрқайсысы бір бірінен құрамы бойынша, немесе орналасу реті бойынша ажыратылатын комбинацияларды айтамыз.

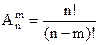(2.1)

мұндағы n! (эн факториал) дегеніміз n!=1· 2 ·3 ·4 ·5 · …· n 1-ден n-ге дейінгі натурал сандардың көбейтіндісі

Ескерту: 0!=1 деген ұйғарым алынған.

Мысал 1.2.1: Әр түсті 6 жалаушадан екеуден ала отырып, неше түрлі белгі беруге болады?

Шешуі: Есеп шартына сәйкес элементтер орналасу реті де, құрамы бойынша да ажыратылатын болғандықтан, орналастыру қолданылады:

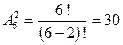
Жауабы:30

2 - анықтама. Берілген әртүрлі n элементтен m элемент бойынша алмастырулар деп әрқайсысы бір бірінен тек орналасу реті бойынша ажыратылатын комбинацияларды айтамыз.

P_n = 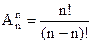= n!яғни

P_n = n!

Мысал 1.2.2: Егер 1, 2, 3 сандарынан әрбір сан кескінге бір рет енетін болса, неше үш орынды сан құруға болады?

Шешуі: Есеп шартына сәйкес элементтер тек орналасу реті бойынша ғана ажыратылатындықтан, алмастыру қолданылады:

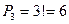
Жауабы: 6

3 - анықтама. Берілген әртүрлі n элементтен m элемент бойынша терулер деп әрқайсысы бір бірінен тек құрамы бойынша ажыратылатын комбинацияларды айтамыз.

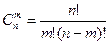
Мысал 1.2.3: Жәшіктегі 10 детальдан 3 детальды неше әдіспен алуға болады?

Шешуі:Есеп шартына сәйкес элементтер құрамы бойынша ажыратылғантықтан теру қолданылады:

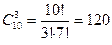
Жауабы: 120

1.3 Геометриялық ықтималдық

Ықтималдықтың классикалық анықтамасының кемшіліктерін жеңу мақсатымен, сынақтар жиыны шектеусіз болғанда геометриялық ықтималдықтар енгізіледі – облысқа (кесінді, жазықтық бөлігі) нүктенің тиісті болу ықтималдығы:

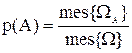
мұндағы Ω – барлық сынақтар жиыны, ал Ω_А- А оқиғасы орындалатын сынақтар жиыны, mes - жиын өлшемі (ұзындық, аудан, көлем т.с.с.).

1.4 Ықтималдықтардың қосу және көбейту теоремалары

Үйлесімсіз оқиғалар ықтималдықтарының қосу теоремасы: Екі үйлесімсіз оқиғалардың біреуінің, қайсысы болса да, бәрібір, орындалу ықтималдығы осы оқиғалар ықтималдықтарының қосындысына тең болады:

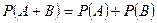
Салдар: Өзара үйлесімсіз бірнеше оқиғалардың біреуінің, қайсысы болса да, бәрібір, орындалу ықтималдығы осы оқиғалар ықтималдықтарының қосындысына тең болады:

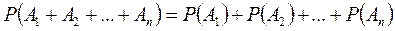
Үйлесімді оқиғалар ықтималдықтарының қосу теоремасы: Екі үйлесімді оқиғалардың ең болмаса біреуінің орындалу ықтималдығы осы оқиғалар ықтималдықтарының қосындысынан оқиғалардың бірлесе орындалу ықтималдығын алып тастағандағы нәтижесіне тең болады:

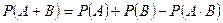
Теорема үйлесімді оқиғалардың кез келген ақырлы санына орынды болады. Мысалы: үш үйлесімді оқиғаға теорема келесі түрде келтіріледі:

Ықтималдықтарды көбейту теоремасы: Екі оқиғаның бірлесе орындалу ықтималдығы біреуінің ықтималдығын екіншісінің, бірінші оқиға орындалды деген ұйғарыммен есептелген шартты ықтималдығына көбейтіндісіне тең болады:,

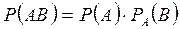
Дербес жағдайда, тәуелсіз оқиғаларға теорема келесі түрде айтылады:

,

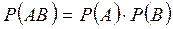басқаша айтқанда, екі тәуелсіз оқиғалардың бірлесе орындалу ықтималдығы осы оқиғалар ықтималдықтарының көбейтіндісіне тең болады.

Салдар: Бірнеше оқиғалардың бірлесе орындалу ықтималдығы біреуінің ықтималдығының басқаларының шартты ықтималдықтарына көбейтіндісіне тең болады және әрбір келесі оқиға ықтималдығы алдыңғы оқиғалар орындалды деген ұйғарыммен есептеледі, яғни:

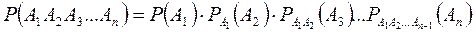
бұл формуладағы 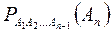- 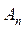оқиғасының оқиғалары орындалды деген ұйғарыммен есептелген ықтималдығы.

Дербес жағдайда, бірнеше тәуелсіз оқиғалардың бірлесе орындалу ықтималдығы, осы оқиғалардың ықтималдықтарының көбейтіндісіне тең болады:

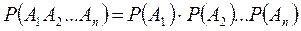
1.5 Толық ықтималдық формуласы және Бейес формуласы

Егер А оқиғасы өзара үйлесімсіз толық топ құрайтын 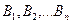оқиғаларының (гипотезалар) біреуі орындалғанда орындалса, онда А оқиғасының орындалу ықтималдығы әр гипотеза ықтималдығының А оқиғасының шартты ықтималдығына көбейтінділерінің қосындысына тең болады:

,

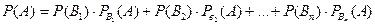бұл формуладағы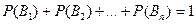

Көрсетілген теңдік толық ықтималдық формуласы деп аталады.

А оқиғасы өзара үйлесімсіз толық топ құрайтын 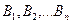оқиғаларының (гипотезалар) біреуі орындалғанда орындалсын.Егер А оқиғасы орындалса, онда гипотезалар ықтималдығы Бейес формуласымен бағаланады:

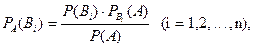
бұл формуладағы

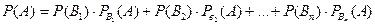
1.6 Сынақтар қайталануы. (Бернулли, Муавр - Лаплас, Пуассон формулалары)

Бернулли формуласы:

Егер А оқиғасының әрбір сынақта орындалу ықтималдығы басқа сынақтар нәтижелерінен тәуелсіз болатын сынақтар жүргізілсе, онда ондай сынақтар А оқиғасына байланысты тәуелсіз сынақтар деп аталады.

Әрқайсысында оқиғаның орындалу ықтималдығы бірдей болатын тәуелсіз сынақтарды қарастырайық.

n тәуелсіз сынақтарда, әрқайсысында оқиғаның орындалу ықтималдығы р – ға тең 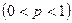, оқиғаның 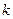рет орындалу ықтималдығы:

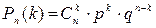
формуласымен табылады. Бұл формуладағы .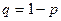

n тәуелсіз сынақтарда оқиғаның

а) 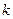реттен кем орындалу ықтималдығы:

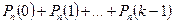
б) 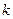реттен артық орындалу ықтималдығы:

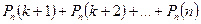
в) 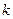реттен кем емес орындалу ықтималдығы:

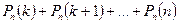
г) 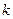реттен артық емес орындалу ықтималдығы:

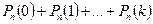
формулаларымен табылады.

Муавр – Лапластың локальдық теоремасы:

n тәуелсіз сынақтарда, әрқайсысында оқиғаның орындалу ықтималдығы р – ға тең 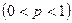, оқиғаның 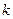рет (қандай ретпен болса да бәрібір) орындалу ықтималдығы жуық мөлшермен (n неғұрлым үлкен болса, соғұрлым дәлірек):

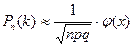
- ке тең болады. Бұл формуладағы

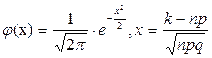
j(x) функциясының кестесі А – қосымшасында келтірілген және j(x) функциясы жұп функция, яғни: j(-x) = j(x).

Муавр – Лапластың интегралдық теоремасы:

n тәуелсіз сынақтарда, әрқайсысында оқиғаның орындалу ықтималдығы р – ға тең 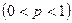, оқиғаның 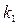реттен кем емес және 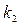реттен артық емес орындалу ықтималдығы жуық мөлшермен:

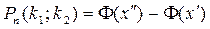
- ке тең болады. Бұл формуладағы

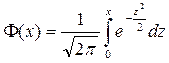- Лаплас функциясы,

Пуассон формуласы:

Әр сынақтағы А оқиғасының орындалу ықтималдығы р-ға тең болатын, n тәуелсіз сынақтар жүргізілсін. Бұл сынақтарда оқиғаның k рет орындалу ықтималдығын табу үшін, Бернулли формуласы қолданылатынын, егер n үлкен болса, Муавр – Лапластың асимтоталық формуласының қолданылатынын көрдік. Енді егер оқиға ықтималдығы аз шама 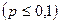болса, онда бұл формула жарамайды. Бұл жағдайларда 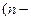үлкен, р- аз) болғанда Пуассонның асимтоталық формуласы қолданылады.

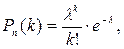мұндағы l=np –ға тең болады.

1.7 Кездейсоқ шамалар

Анықтама. Кездейсоқ шама деп сынақ нәтижесінде қандай да бір мән (тек бір ғана) қабылдайтын шаманы айтамыз, әрі оның алдын-ала, сынақ жүргізілгенге дейін, қандай мән қабылдайтыны белгісіз.

Кездейсоқ шаманың қабылдайтын мәндері ақырлы бүтін сандар немесе тізбек түрінде жазылса, онда ондай кездейсоқ шамаларды дискреттік шамалар деп атаймыз.

Дискретті кездейсоқ шамалар үлестірім түрлері:

1 Биномдық үлестірім

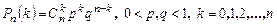
2 Пуассон үлестірімі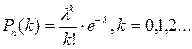

3 Геометриялық үлестірім

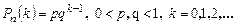
4 Гипергеометриялық үлестірім

.

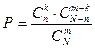Егер кездейсоқ шама өзінің мүмкін мәндерін [a, b] интервалынан қабылдаса және бұл мәндерді бүтін сандармен нөмірлеуге болмаса, онда ол үздіксіз кездейсоқ шама аталады.

Дата добавления: 2014-11-08