
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комбинаторика формулалары 2 страница
|
|
|
|
Үздіксіз кездейсоқ шамалар үлестірім түрлері:
1 Бірқалыпты үлестірім
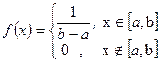 ,
,  .
.
2 Қалыпты үлестірім (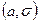 параметрлерімен берілген)
параметрлерімен берілген)
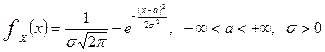
3 Көрсеткіштік үлестірім
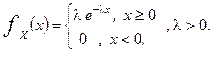
Дискретті кездейсоқ шамалардың үлестірім заңы:
Х кездейсоқ шамасын толық анықтау үшін, Х-тің мүмкін мәндерінен басқа, осы мүмкін мәндер мен оған сәйкес ықтималдықтарының арасындағы байланысты көрсету қажет. Бұл байланыс Х шамасыныңүлестірім заңы деп аталады және дискретті кездейсоқ шама үшін оны мынадай үлестірім қатары түрінде беруге болады:
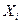
| 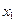
| 
| … | 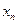
|
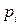
| 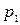
| 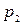
| … | 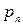
|
Бір сынақта кездейсоқ шаманың бір мән қабылдайтынын ескере отырып,

оқиғалары толық топ құрайды деп ұйғарамыз, ендеше кестенің екінші жолындағы ықтималдықтар қосындысы:
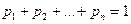
Сонымен қатар, бұл байланысты график түрінде үлестірім көпбұрышы ретінде беруге болады.
Үздіксіз кездейсоқ шамалардың үлестірім заңы:
Үздіксіз Х кездейсоқ шамасының үлестірім заңдылығы үлестірім функциясы (интегралдық функция) арқылы беріледі.
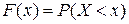 .
.
Солнымен, үлестірім функциясы кездейсоқ шама X сынақ нәтижесінде x – тен кіші мәнге ие болу ықтималдығын анықтайды.
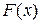 үлестірім функциясының қасиеттері:
үлестірім функциясының қасиеттері:
1. 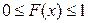
2. 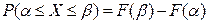
3. 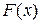 - кемімелі емес функция
- кемімелі емес функция
4. 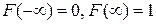 .
.
Үздіксіз Х шамасының үлестірімінің әртүрлі нүктелердің маңайындағы сипаттамаларын 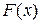 функциясына қарағанда үлестірім тығыздығы (дифференциалдық функция):
функциясына қарағанда үлестірім тығыздығы (дифференциалдық функция):
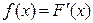
толығырақ сипаттайды.
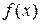 үлестірім тығыздығының қасиеттері
үлестірім тығыздығының қасиеттері
1. 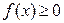
2. 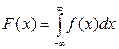
3. 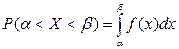
4. 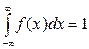
1.8 Кездейсоқ шамалардың сандық сипаттамалары
Х кездейсоқ шамасының математикалық күтімі деп
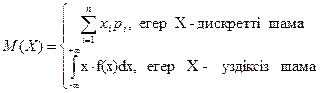
формуласымен анықталатын шаманы айтамыз. Математикалық күтімнің төмендегідей қасиеттері бар:
1. M(C)=C;
2. M(CX)=C M(X);
3. M(X+Y)=M(X)+M(Y),
бұл формулалардағы С - тұрақты шама; X,Y – кездейсоқ шамалар.
Х кездейсоқ шамасының дисперсиясы деп
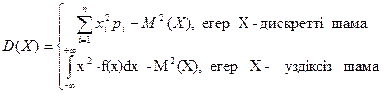
формуласымен анықталатын шаманы айтамыз. Дисперсияның төмендегідей қасиеттері бар:
1.D(C)=0;
2. D(CX)=C2 D(X);
3. D(X+Y)=D(X)+D(Y);
4. D(X)³0,
бұл формулалардағы С - тұрақты шама; X,Y – кездейсоқ шамалар.
Орта квадраттық ауытқудеп:
s= 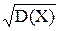
формуласы бойынша есептелінетін шаманы айтамыз.
Кездейсоқ шаманың моменттері:
Х кездейсоқ шамасының k ретті алғашқы моменті nk деп
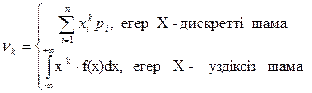
формуласымен анықталатын шаманы айтамыз.
Х кездейсоқ шамасының k-шы ретті орталық моменті mk деп:
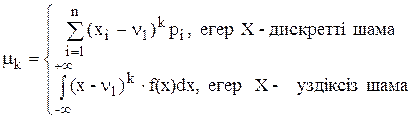
формуласымен анықталатын шаманы айтамыз.
Алғашқы және орталық момент арасында мынадай байланыс бар:
m2 = n2 - n12;
m3=n3 - 3n1 n2+2n13;
m4=n4-4n3n1+6n2n12-3n14.
Үлестірім заңдылығының асимметриясы мен эксцессі:
Үлестірім заңдылығының асимметриясын 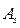 арқылы белгілейміз:
арқылы белгілейміз:
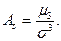
Үлестірім заңдылығының эксцессін 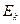 арқылы белгілейміз:
арқылы белгілейміз:
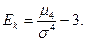
2 ЕСЕПТЕУ ТАПСЫРМАЛАРЫН ОРЫНДАУ ҮЛГІСІ
2.1 Геометриялық ықтималдық
2.1.1- мысал: Радиустары 6 см және 4 см болатын концентрлі екі шеңбер берілген. Егер нүктенің шеңберге түсу ықтималдығы шеңбер ауданына пропорционал болса және орналасуына байланысты емес болса, онда үлкен дөңгелекке лақтырылған нүктенің үлкен және кіші дөңгелек арасында пайда болған сақинаға түсу ықтималдығын табыңыз.
Шешуі:А оқиғасы – «үлкен дөңгелекке лақтырылған нүктенің сақинаға түсуі». Лақтырылған нүкте үлкен дөңгелекке түсуі мүмкін, барлық сынақтар жиыны үлкен дөңгелек ауданы: 36pR2. Ал сақинаның ауданы 36pR2 -16pR2 =20pR2 . Яғни, бұл А оқиғасын қанағатттандыратын сынақтар жиыны. Ендеше, р(А)= 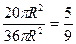 .
.
Жауабы: 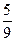
2.1.2 - мысал: Екі оқиғаның кездейсоқ басталу уақыты 1100 – сағаттан 1300 сағатқа дейін.
Оқиғаның біреуі 10 минутқа, екіншісі 15 минутқа созылады.
а) оқиғалардың уақытпен қиылысу ықтималдығын;
б) оқиғалардың уақытпен қиылыспау ықтималдығын табу керек.
                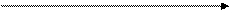 Шешуі: Шешуі:
 у
х
15 120 у
х
15 120
| А- оқиғалардың уақытпен қиылысуы;
Оқиғалардың басталу моментін сәйкесінше x және y деп белгілейік. x пен y тің мүмкін мәндер жиыны 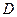 - келесі теңсіздіктермен анықталады: - келесі теңсіздіктермен анықталады:
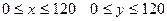 11 –ді уақыттың басталуы деп қабылдағанбыз, уақыт минутпен есептеледі. Ендеше x пен y тің қиылысуының мәндер жиыны
11 –ді уақыттың басталуы деп қабылдағанбыз, уақыт минутпен есептеледі. Ендеше x пен y тің қиылысуының мәндер жиыны  келесі теңсіздіктермен анықталады: келесі теңсіздіктермен анықталады:
|
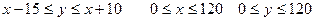 ;
;
Әрбір x;y мәндер жұбына тік бұрышты координаталар жүйесінің жазықтығындағы (x;y) нүктесі сәйкестендірейік.
Ендеше 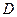 жиынына қабырғасы 120 болатын квадрат сәйкес келеді, ал
жиынына қабырғасы 120 болатын квадрат сәйкес келеді, ал  жиынына:
жиынына:
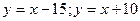
түзулері арасындағы квадраттың жолағы сәйкес келеді. Сөйтіп, А оқиғасының ықтималдығы:
а) геометриялық ықтималдықтың анықтамасы бойынша:
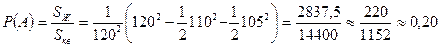
түрінде табылады.
б) В-оқиғалардың уақытпен қиылыспауы;
Бұл А оқиғасына қарама қарсы оқиға, ендеше оқиғаның орындалу ықтималдығы келесі түрде табылады:
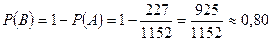
Жауабы: 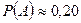 ;
; 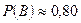
2.2 Ықтималдықтардың қосу және көбейту теоремалары
2.2.1 - мысал Кітапханада 18 оқулық бар, олардың бесеуі түптелген. Кітапханашы кез келген үш оқулықты алды. Алынған оқулықтың ең болмаса біреуінің түптелген оқулық болу ықтималдығын табу керек.
Шешуі:А оқиғасы – «алынған үш оқулықтың ең болмаса біреуінің түптелген оқулық болуы; В оқиғасы –«алынған үш оқулықтың біреуі түптелген оқулық болуы»; С оқиғасы - «алынған үш оқулықтың екеуі түптелген оқулық болуы»; D оқиғасы - «алынған үш оқулықтың үшеуі де түптелген оқулық болуы».
Ізделінген А оқиғасы оқиғалар қосындысы түрінде келтіріледі, яғни
A=B+C+D
Қосу теоремасы бойынша:
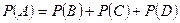
В, С, D оқиғаларының ықтималдығын табалық:
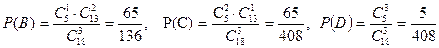
Ендеше 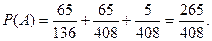
2.2.2 - мысал Құрылғы тәуелсіз жұмыс жасайтын үш элементтен тұрады. Бірінші, екінші, үшінші элементтердің тоқтамай ақаусыз жұмыс жасау ықтималдықтары сәйкесінше 0,6; 0,7; 0,8. Белгілі уақыт мерзімінде а) тек бір элемент ақаусыз жұмыс жасау ықтималдығын; б) тек екі элемент ақаусыз жұмыс жасау ықтималдығын; в) үш элементте ақаусыз жұмыс жасау ықтималдығықтарын табу керек.
Шешуі:
а) А- «тек бір элемент ақаусыз жұмыс жасау» оқиғасы
А1 - «бірінші элемент ақаусыз жұмыс жасау» оқиғасы
А2 - «екінші элемент ақаусыз жұмыс жасау» оқиғасы
А3-«үшінші элемент ақаусыз жұмыс жасау» оқиғасы болсын.
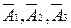 сәйкесінше А1, А2, А3 оқиғаларына қарама-қарсы оқиғалар.
сәйкесінше А1, А2, А3 оқиғаларына қарама-қарсы оқиғалар.
А оқиғасын А!, А2, А3 оқиғалары арқылы былай өрнектеуге болады:
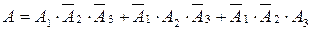 .
.
Есептің берілу шарты бойынша:
 ,
,
онда
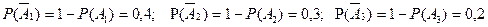
болады.
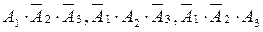 оқиғалары өзара үйлесімсіз және А!, А2, А3 оқиғалары өзара тәуелсіз, ендеше ықтималдықтарды қосу және көбейту теоремаларын қолдансақ:
оқиғалары өзара үйлесімсіз және А!, А2, А3 оқиғалары өзара тәуелсіз, ендеше ықтималдықтарды қосу және көбейту теоремаларын қолдансақ:
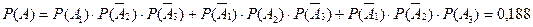 .
.
б) В- «тек екі элемент ақаусыз жұмыс жасау» оқиғасы
А1 - «бірінші элемент ақаусыз жұмыс жасау» оқиғасы
А2 - «екінші элемент ақаусыз жұмыс жасау» оқиғасы
А3-«үшінші элемент ақаусыз жұмыс жасау» оқиғасы болсын.
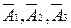 сәйкесінше А1, А2, А3 оқиғаларына қарама-қарсы оқиғалар.
сәйкесінше А1, А2, А3 оқиғаларына қарама-қарсы оқиғалар.
В оқиғасын А!, А2, А3 оқиғалары арқылы былай өрнектеуге болады:
 .
.
Есептің берілу шарты бойынша:
 ,
,
онда
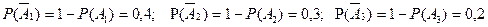
болады.
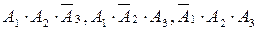 оқиғалары өзара үйлесімсіз және А!, А2, А3 оқиғалары өзара тәуелсіз, ендеше ықтималдықтарды қосу және көбейту теоремаларын қолдансақ:
оқиғалары өзара үйлесімсіз және А!, А2, А3 оқиғалары өзара тәуелсіз, ендеше ықтималдықтарды қосу және көбейту теоремаларын қолдансақ:
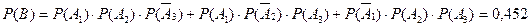 .
.
в) С - «үш элементте ақаусыз жұмыс жасау» оқиғасы
А1 - «бірінші элемент ақаусыз жұмыс жасау» оқиғасы
А2 - «екінші элемент ақаусыз жұмыс жасау» оқиғасы
А3-«үшінші элемент ақаусыз жұмыс жасау» оқиғасы болсын.
С оқиғасын А!, А2, А3 оқиғалары арқылы былай өрнектеуге болады:
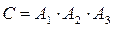 .
.
Есептің берілу шарты бойынша:
 ,
,
А!, А2, А3 оқиғалары өзара тәуелсіз, ендеше тәуелсіз оқиғаларды көбейту теоремасын қолдансақ:
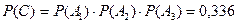 .
.
2.3 Толық ықтималдық формуласы және Бейес формуласы
2.3.1 - мысал Пирамидада 5 мылтық бар, олардың үшеуі оптикалық көздеуі бар мылтық. Мергеннің нысанаға оптикалық көздеуі бар мылтықпен тигізуі 0,95 –ке тең, оптикалық көздеуі жоқ мылтықпен нысанаға тигізу ықтималдығы 0,7 – ге тең.
1) Мергеннің кездейсоқ алынған мылтықпен нысанаға тигізу ықтималдығын табу керек;
2) Мергеннің нысанаға оптикалық көздеуі бар мылтықпен тигізу ықтималдығын табу керек;
3) Мергеннің нысанаға оптикалық көздеуі жоқ мылтықпен тигізу ықтималдығын табу керек.
Шешуі:
А- нысанаға оқ тигізілді деген оқиға болсын.
Мылтық туралы екі гипотеза қарастырылады:
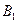 - нысанаға оптикалық көздеуі бар мылтықпен ату жүргізілді;
- нысанаға оптикалық көздеуі бар мылтықпен ату жүргізілді;
 нысанаға оптикалық көздеуі жоқ мылтықпен ату жүргізілді.
нысанаға оптикалық көздеуі жоқ мылтықпен ату жүргізілді.
Нысанаға оптикалық көздеуі бар мылтықпен ату жүргізілді деген оқиға ықтималдығы:
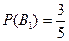
Нысанаға оптикалық көздеуі жоқ мылтықпен ату жүргізілді деген оқиға ықтималдығы:
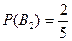
1)Ендеше нысанаға кез келген мылтықпен оқ тиді деген оқиға ықтималдығы:
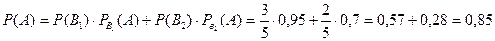
2) Нысанаға оптикалық көздеуі бар мылтықпен тигізілді деген оқиға ықтималдығы:
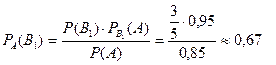
3) Нысанаға оптикалық көздеуі жоқ мылтықпен тигізілді деген оқиға ықтималдығы:
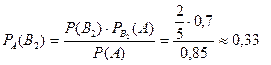
2.4 Сынақтар қайталануы. (Бернулли, Муавр - Лаплас, Пуассон формулалары)
Бернулли формуласы:
2.4.1 - мысал Цехта 6 мотор жұмыс жасайды. Әрбір мотор үшін, оның уақытында жұмыс жасап тұру ықтималдығы 0,8 – ге тең. Берілген уақытта: а) 4 мотор жұмыс жасап тұруы; б) 3 мотордан кем моторлар жұмыс жасап тұруы; в) 5 мотордан артық моторлардың жұмыс жасауы ықтималдықтарын табу керек.
Шешуі: а) Әрбір мотор үшін, оның уақытында жұмыс жасап тұру ықтималдығы тұрақты, р = 0,8 – ге тең.
4 мотор да жұмыс жасап тұру оқиғасының. ықтималдығы Бернулли формуласы бойынша:
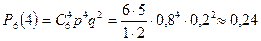
болады.
б) 3 мотордан кем моторлардың жұмыс жасап тұру ықтималдығы:
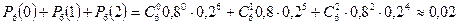
болады.
в) 5 мотордан артық моторлардың жұмыс жасауы ықтималдығы:
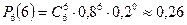
болады.
Муавр – Лапластың локальдық теоремасы:
Мысал 2.4.2 Егер А оқиғасының әр сынақта орындалу ықтималдығы р = 0,2 –ге тең болса, онда 200 тәуелсіз сынақтарда А оқиғасының а) 40 рет орындалу ықтималдығын; б) 60 реттен 80 ретке дейін орындалу ықтималдықтарын табу керек.
Шешуі: а) есеп шарты бойынша:
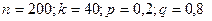
Муавр Лапластың асимптоталық формуласын қолданайық:
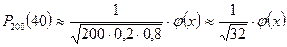
x – тің мәндерін есептейік:
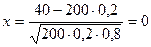 .
.
А.1 кестесінен
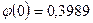
екендігін таптық, осыдан ізделінген ықтималдық келесі болады:
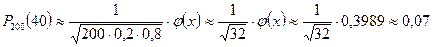
б) 60 реттен 80 ретке дейін орындалу ықтималдығын табайық, есеп шарты бойынша:
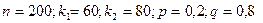
Муавр Лапластың интегралдық формуласын қолданайық:
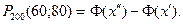
Интегралдың жоғарғы және төменгі шектерін есептейік:
 ;
;
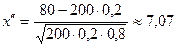 .
.
Сонымен, келесі нәтиже алдық:
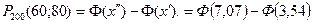
Б.1 кестесінен
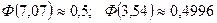
екендігін таптық; осыдан ізделінген ықтималдық келесі болады:
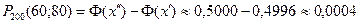
Пуассон формуласы:
Мысал 2.4.3 Фабрикадан 5000 сапалы бұйым келіп түсті. Бұйымның тасымалдау кезінде зақымдалу ықтималдығы 0,0002. Фабрикаға әкелінген бұйымның үшеуінің зақымдалу ықтималдығын табу керек.
Шешуі: а) есеп шарты бойынша:
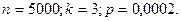
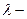 ны есептеп алайық:
ны есептеп алайық:
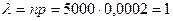 .
.
Ендеше, ізделінген оқиға ықтималдығы жуық шамамен келесі болады:
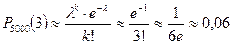
2.5 Кездейсоқ шамалар
Мысал 2.5.1 Партиядағы 8 детальдың 6 стандартқа жататын детальдар. Кездейсоқ 2 деталь таңдалды. Таңдалған детальдар арасындағы стандартқа жататын детальдар саны болатын кездейсоқ шаманың үлестірім заңын құрыңыз:
Шешуі: Кездейсоқ шама X - таңдалған детальдар арасындағы стандартқа жататын детальдар саны, X- тің мүмкін мәндері келесідей болады:
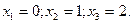
X- тің мүмкін мәндерінің ықтималдықтарын келесі формуламен табамыз:
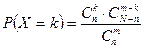 ,
,
бұл формуладағы N – партиядағы детальдар саны, n – партиядағы стандартты детальдар саны, m – таңдалған детальдар саны, k - таңдалған детальдар арасындағы стандартқа жататын детальдар саны.
Табайық:
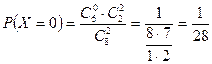
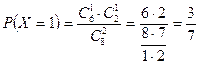
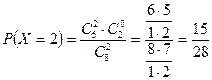
Ізделінген үлестірім заңын құрайық:
| X | |||
| p | 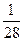
| 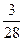
| 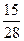
|
Бақылау: 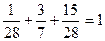
2.6 Кездейсоқ шамалардың сандық сипаттамалары
Мысал 2.6.1 Келесі үлестірім заңдылығымен берілген дискретті кездейсоқ шаманың математикалық күтімін, дисперсиясын және орта квадрат ауытқуын табу керек:
| X | -4 | ||
| p | 0,2 | 0,3 | 0,5 |
Шешуі: Дискретті кездейсоқ шаманың математикалық күтімі X- тің мүмкін мәндерінің ықтималдықтарына көбейтінділерінің қосындысына тең болады:
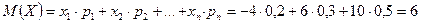
Дискретті кездейсоқ шаманың дисперсиясын келесі формуламен есептеу тиімдірек:
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 2796; Нарушение авторских прав?; Мы поможем в написании вашей работы!