
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однофакторный дисперсионный анализ
|
|
|
|
Рассмотрим несколько наиболее распространенных вариантов эксперимента, организуемого для проведения дисперсионного анализа: однофакторный, двухфакторный и трехфакторный анализ с разным числом уровней факторов и разным числом опытов на каждом уровне.
Однофакторный эксперимент (один фактор А)
Значения измеряемого признака – Х 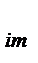 .
.
1.Эксперимент на двух уровнях, i =1,2 (рис а):
- без повторных опытов, m = 1;
- c повторными опытами, одинаковое число опытов на каждом уровне,
m = 1,2,…,n.
- c повторными опытами, разное число опытов на каждом уровне
m = 1,2,…,n 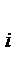 .
.
2.Эксперимент на нескольких уровнях, i =1,2,…,a (рис.б):
- без повторных опытов, m = 1;
- c повторными опытами, одинаковое число опытов на каждом уровне
m = 1,2,…,n;
- c повторными опытами, разное число опытов на каждом уровне
m = 1,2,…, n 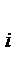 .
.
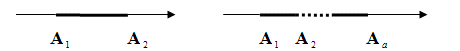
а) б)
Рис.Точки эксперимента в однофакторном анализе: а) два уровня А 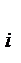 , i =1,2; б) несколько уровней А
, i =1,2; б) несколько уровней А 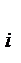 , i =1,2,…,a
, i =1,2,…,a
Таблица представляет исходные данные однофакторного эксперимента на двух уровнях с одинаковым числом повторных опытов. Число групп (H) равно числу уровней: A 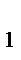 , A
, A 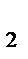 ; i=1,2.
; i=1,2.
Данные для однофакторного анализа, равное число опытов
| Уровни (группы) | Результаты опытов: X 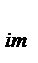 , m = 1,2,…n , m = 1,2,…n
| ||||
X 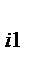
| … | X 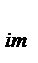
| … | X 
| |
A 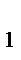
| X 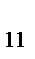
| … | X 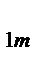
| … | X 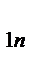
|
A 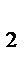
| X 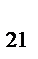
| … | X 
| … | X 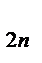
|
Лекция 2 Понятие о многофакторном дисперсионном анализе.
Двухфакторный эксперимент (факторы А и В)
Значения измеряемого признака - Х 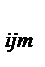 .
.
Эксперимент на нескольких уровнях, i =1,2,…,a; j = 1,2,…,b:
- без повторных опытов, m = 1;
- c повторными опытами, одинаковое число опытов на каждом ij- уровне, m 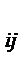 = 1,2,…,n;
= 1,2,…,n;
- c повторными опытами, разное число опытов на каждом ij-уровне, m 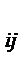 = 1,2
= 1,2
Таблица 1Данные для двухфакторного анализа на двух уровнях, разное число опытов
| № строки (группы) | Сочетания уровней А В | Результаты опытов: Х 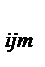 ; m = 1,2,…n ; m = 1,2,…n 
| |||||
X 
| … | X 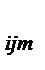
| … | X 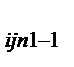
| X 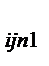 
| ||
| 1; 1 | X 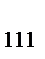
| … | X 
| … | X 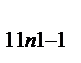
| X 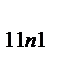
| |
| 1; 2 | X 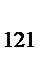
| … | X 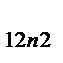
| _ | _ | _ | |
| 2; 1 | X 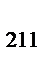
| … | X 
| … | X 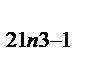
| X 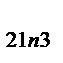
| |
| 2; 2 | X 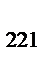
| … | X 
| … | X 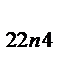
| _ |
Таблица 2 Данные для двухфакторного анализа на нескольких уровнях, равное число опытов
| № строки | Сочетания уровней А В | Наблюденные значения признака в группах, X 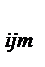
| ||||
| 1-й опыт | … | m- опыт | … | n-опыт | ||
| 1; 1 | X 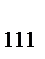
| … | X 
| … | X 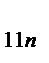
| |
| 1; 2 | X 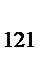
| … | X 
| … | X 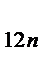
| |
| … | … | … | … | … | … | … |
| ij | i; j | X 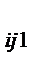
| … | X 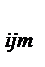
| … | X 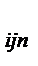
|
| … | … | … | … | … | … | … |
| H | а; b | X 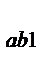
| … | X 
| … | X 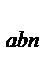
|
Число групп (H) равно числу перестановок уровней: ij = 1,2,…,H
Модель однофакторного дисперсионного анализа.
Основное уравнение дисперсионного анализа:
SS = SS 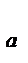 + SSε (12.7)
+ SSε (12.7)
Одинаковое число повторных опытов (m = 1,2,…,n):
SS = 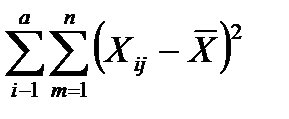 (12.8)
(12.8)
где SS - общая сумма квадратов разностей наблюдений и их среднего значения;
SS 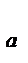 = n
= n 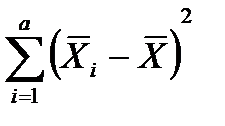 (12.9)
(12.9)
где SS  - сумма квадратов между группами (вклад в общую сумму квадратов, обусловленный различиями в уровнях фактора А);
- сумма квадратов между группами (вклад в общую сумму квадратов, обусловленный различиями в уровнях фактора А);
SS 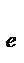 =
= 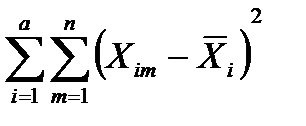 , (12.10)
, (12.10)
где SS 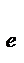 - сумма квадратов внутри групп – остаток, вклад в общую сумму квадратов, вызванный случайной изменчивостью данных внутри групп (или сумма квадратов случайных эффектов - ошибка опыта).
- сумма квадратов внутри групп – остаток, вклад в общую сумму квадратов, вызванный случайной изменчивостью данных внутри групп (или сумма квадратов случайных эффектов - ошибка опыта).
 =
= 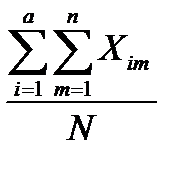 , (12.11)
, (12.11)
где  - общее среднее, N = an – общее число опытов;
- общее среднее, N = an – общее число опытов;
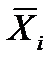 =
= 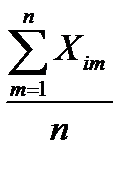 , (12.12)
, (12.12)
где 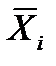 - среднее значение на i уровне фактора А.
- среднее значение на i уровне фактора А.
Разное число повторных опытов (m =1,2,…,n 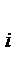 ):
):
SS = 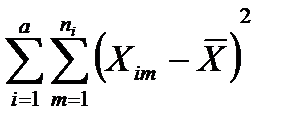 ; SS
; SS 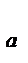 =
= 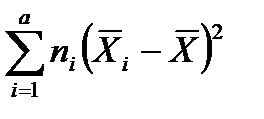 ; SS
; SS 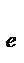 =
= 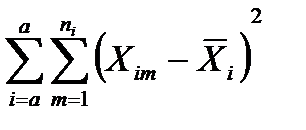 ; (12.13)
; (12.13)
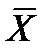 =
= 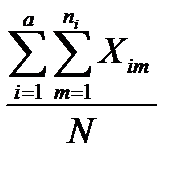 ; N =
; N = 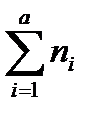 ;
; 
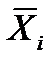 =
= 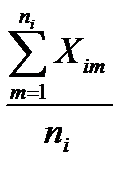 (12.14)
(12.14)
Оценки дисперсий и определение числа степеней свободы
S 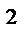 =
= 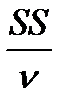 - оценка общей дисперсии;
- оценка общей дисперсии;  ν = N - 1 - число степеней свободы при определении общей дисперсии;
ν = N - 1 - число степеней свободы при определении общей дисперсии;
S  =
= 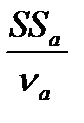 - оценка дисперсии по уровням фактора А; ν
- оценка дисперсии по уровням фактора А; ν 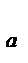 = a –1 - число степеней свободы фактора А;
= a –1 - число степеней свободы фактора А;
S 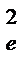 =
= 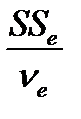 - остаточная оценка дисперсии (дисперсия ошибки);
- остаточная оценка дисперсии (дисперсия ошибки);
ν 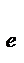 = N – a - число степеней свободы при определении ошибки.
= N – a - число степеней свободы при определении ошибки.
ν = ν 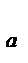 + ν
+ ν 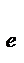 = N – 1 = (a –1) + (N – a) (12.15)
= N – 1 = (a –1) + (N – a) (12.15)
Проверка H 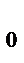 - гипотезы
- гипотезы
Расчетное значение критерия:
F 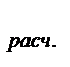 =
= 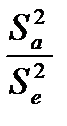 . (12.16)
. (12.16)
Критическое значение F  определяется по прил.4 при α, ν
определяется по прил.4 при α, ν 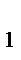 = ν
= ν 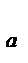 и ν
и ν 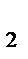 = ν
= ν 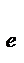 . Если
. Если
F 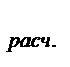
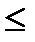 F
F  при α, ν
при α, ν 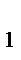 , ν
, ν 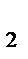 , (12.16)
, (12.16)
то гипотеза H 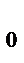 - принимается. В противном случае – отклоняется.
- принимается. В противном случае – отклоняется.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 730; Нарушение авторских прав?; Мы поможем в написании вашей работы!