Тренд динамического ряда

Большое количество данных в экономике, коммерции, технике и т.д. могут рассматриваться как в пространстве, так и во времени, путем построения и анализа одного или нескольких временных рядов.

Тренд динамического ряда.

Понятие экономического временного ряда и его составляющие.

Тема 15. Статистический анализ временных рядов

Определим дискретный временной ряд как последовательность измерений значений переменной (процесса) за определенный период через одинаковые промежутки времени:

Z₁, Z₂, Z₃,…Z_t,…, Z_n. (14.1)

Последовательные наблюдения в (4.7.1) обычно зависимы. С детерминистской точки зрения (4.4.7.1) можно представить как:

Z _t = f(t) + ε_t,

где t=1,2,…,n;

f- гладкая (непрерывная и дифференцируемая) функция, характеризующая долгосрочное движение в зависимости от времени - тренд;

ε_t - случайный ряд возмущений, наложенный на систематическую часть.

При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционная зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на один или несколько шагов во времени, называемого коэффициентом автокорреляции.

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка τ, то ряд содержит циклические или сезонные колебания с периодичностью в t моментов времени. Если ни один коэффициент не является значимым, можно сделать вывод о том, что либо ряд не содержит тенденции и циклических колебаний, либо содержит сильную не линейную тенденцию.

Число периодов или моментов времени, по которым рассчитывается коэффициент автокорреляции, называют лагом.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Тенденция во времени может принимать разные формы.

Анализ временных рядов преследует целый ряд целей:

описание поведения ряда;

построение модели для объяснения наблюдений.

В общем случае можно предположить в трендовой модели наличие следующих компонент:

тренд или долгосрочное колебание;

регулярное движение относительно тренда;

сезонная компонента;

остаток.

Модель, в которой временной ряд представлен как сумма перечисленных выше компонент, называется аддитивной моделью временного ряда. Если временной ряд представлен как произведение компонент, то она называется мультипликативной моделью временного ряда.

Приложение Е – Глоссарий

Автокорреляция – корреляция между уровнями временного ряда или отклонениями от тренда, сдвинутыми во времени на определенный период.

Альтернативная гипотеза – обозначается 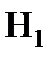, содержит утверждение, обратное утверждению основной гипотезы, и считается истинным, если основная гипотеза оказывается ложной.

Асимметрия – скошенность частот вариационного ряда вправо или влево от среднего значения признака.

Биноминальное распределение вероятностей – используется для вычисления вероятности определенного числа успехов из заданного числа испытаний.

Вариационный ряд – упорядоченная совокупность значений признака и соответствующих им частот или частностей.

Вариация – колеблемость, изменение величины признака в статистической совокупности.

Вероятность – численная мера возможности, того произойдет ли определенное событие.

Взаимоисключающие события – когда два события не могут произойти одновременно в рамках одного эксперимента.

Выборка – подмножество генеральной совокупности.

Генеральная совокупность – представляет все возможные исходы или измерения, представляющие для нас интерес.

Гипотеза альтернативная (конкурирующая) – гипотеза, противоположная нулевой гипотезе.

Гипотеза нулевая – выдвинутая гипотеза, справедливость которой проверяется.

Гипотеза статистическая – непротиворечивое предположение о свойстве генеральной совокупности, проверяемое по данным выборки.

Гистограмма – график, демонстрирующий число наблюдений в каждой группе в виде прямоугольников определенной высоты.

Данные – значения, приписываемые наблюдению или измерению, основной элемент статистического анализа.

Дискретное распределение вероятностей – перечень всех возможных исходов эксперимента для дискретной случайной величины вместе с относительной частотой или вероятностью.

Дисперсионный анализ – процедура проверки разности двух или более средних не генеральной совокупности, устанавливает структуру связи между результативным признаком и факторными признаками.

Дисперсия – характеристика колеблемости индивидуальных значений от математического ожидания или среднего значения.

Доверительный интервал – интервал значений, используемый для оценки параметра совокупности и связанный с определенным доверительным уровнем.

Доверительный уровень – вероятность того, что интервальная оценка будет покрывать заданный параметр совокупности.

Зависимая переменная – переменная, обозначаемая у в уравнении регрессии, на которое оказывает влияние независимая переменная.

Зависимые выборки – наблюдаемые данные из одной выборки связаны с данными из другой выборки.

Закон больших чисел – совокупность теорем теории вероятностей о математическом ожидании случайной величины.

Закон распределения случайной величины – всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Значимость, статистическая существенность связи или ее характеристик, утверждается при отклонении нулевой гипотезы об отсутствии связи (о равенстве нулю параметров, измеряющих связь) с заданной вероятностью ошибки.

Измерение центральной тенденции – описывает центральную точку нашего набора данных с помощью одного значения.

Исход – определенный результат эксперимента или опыта.

Корреляция – зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Коэффициент корреляции – указывает на тесноту и направление линейной связи зависимой и независимой переменными.

Критерий значимости – величина, взятая из выборки, используемая для принятия решения об отклонении или принятий основной гипотезы.

Кумулята – графическое изображение функции распределения вероятностей или накопленных частот вариационного ряда.

Математическое ожидание случайной величины – сумма произведений всех возможных значений случайной величины на вероятности этих значений.

Медиана – значение из данных ряда распределения, по отношению к которому половина единиц наблюдения имеет большее значение, а половина – меньшее.

Метод моментов – один из общих методов оценивания неизвестных параметров совокупности.

Метод наименьших квадратов – статистический метод нахождения оценок параметров генеральной совокупности.

Мода – значение в вариационном ряду, встречающееся чаще всего.

Наблюдаемые частоты – число фактических наблюдений, определенного каждого значения или интервала значений переменной.

Независимая переменная – переменная, обозначаемая х в уравнении регрессии; предполагается, что она влияет на зависимую переменную.

Независимые выборки – данные из одной выборки не связаны с наблюдаемыми данными из другой выборки.

Независимые события – реализация События В никоем образом не влияет на реализацию События А.

Непрерывная случайная переменная – переменная, которая может принимать любое числовое значение в пределах заданного интервала в результате наблюдения за исходом эксперимента.

Однофакторный дисперсионный анализа – дисперсионный анализ, предусматривающий анализ веления одного фактора на изменение зависимой переменной.

Оценка интервальная – оценка параметра генеральной совокупности в виде интервала, концами которого являются точечные оценки.

Оценка точечная – приближенное значение неизвестного параметра генеральной совокупности задаваемое одним числом.

Основная (нулевая) гипотеза – обозначается , это выдвинутая гипотеза экспериментатором.

Ошибка второго рода – когда основная гипотеза принимается, а на самом деле она является ложной.

Ошибка выборки – когда измерение по выборке отличается от измерения по генеральной совокупности.

Ошибка первого рода - когда основная гипотеза отклоняется, хотя на самом деле она является истинной.

Параметр – числовая характеристика совокупности.

Плотность распределения вероятностей непрерывной случайной величины называется производная от ее функции распределения.

Правило сложения вероятностей – определяется вероятность объединения двух или более событий.

Правило умножения вероятностей – определяет вероятность пересечения двух или более событий.

Произведение событий – событие, заключающееся в совместном появлении всех этих событий.

Простая случайная выборка – выборка, отобрана из любых элементов генеральной совокупности.

Противоположные события – два несовместных события, образующие полную группу.

Размах – разность между наибольшим и наименьшим значением вариационного ряда.

Ряд распределения – совокупность значений случайной величины и соответствующих им вероятностей.

Случайная величина – переменная, которая в результате опыта принимает то или иное заранее неизвестное значение.

Событие – один или более исходов, представляющий интерес для эксперимента и являющихся подмножеством выборочного пространства.

События несовместные – если никакие два из этих событий не могут появиться вместе в одном испытании.

Средняя квадратическая ошибка среднего – средняя из квадратов отклонений средних по выборке.

Среднее квадратическое отклонение – показатель вариации, вычисляемой путем извлечения квадратного корня из дисперсии.

Статистическая оценка – функция от наблюдаемых случайных величин.

Статистический вывод – используется для того, чтобы делать выводы применительно к генеральной совокупности на основе выборки данных их этой совокупности.

Степень свободы – число значений, которые могут свободно варьироваться, если известна определенная информация, например, среднее по выборке.

Статистическая гипотеза – это всякое высказывание о генеральной совокупности, проверяемое по выборке.

Сумма событий – событие, заключающееся в появлении хотя бы одного из этих событий.

Теория массового обслуживания – изучает математические модели различных систем массового обслуживания.

Теснота связи – качественная характеристика степени зависимости между изучаемыми признаками.

Точечная оценка – значение, точнее всего описывающее интересующую нас совокупность; чаще всего в этом качестве используется среднее.

Уравнение регрессии – функция, описывающая изменения зависимой переменной в связи с изменениями значений независимых переменных.

Уровень значимости – вероятность совершения ошибки первого рода.

Условная вероятность – вероятность события А при том, что событие В уже произошло.

Фактор – причина, находящаяся в определенной логической связи со следствием;показатель,находящийся в количественно определенной взаимосвязи с другим показателем.

Функция распределения вероятностей случайной величины х называется функция F (x), выражающая вероятность того, что х примет значение, меньше х.

Функция случайного аргумента – случайная величина,получаемая детерминированным преобразованием случайной величины Х.

Центральная предельная теорема – теорема гласит, что по мере увеличения размера выборки (n) среднее по выборке стремится следовать нормальному закону распределения вероятностей.

Частость – относительная величина, определяющая долю частот отдельных вариантов или интервалов в общей сумме частот.

Частота – абсолютное число, показывающее, сколько раз встречается в совокупности то или иное значение признака.

Шкала графика – совокупность линий, отметок и проставленных у некоторых из них чисел отсчета или других символов, соответствующих ряду последовательных значений изображаемых величин.

Эксцесс – числовая характеристика островершинности или «крутости» статистического распределения.

Приложение Ж – Экзаменационные билеты

Дата добавления: 2014-11-20