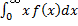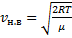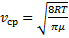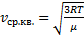КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные случаи
|
|
|
|
Рассмотрим несколько частных случаев:
1. Если  , то это означает, что тепло к системе подводится.
, то это означает, что тепло к системе подводится.
2. Если 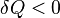 , аналогично — тепло отводится.
, аналогично — тепло отводится.
3. Если  , то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.
, то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.
Обобщая: в конечном процессе 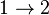 элементарные количества теплоты могут быть любого знака. Общее количество теплоты, которое мы назвали просто
элементарные количества теплоты могут быть любого знака. Общее количество теплоты, которое мы назвали просто  — это алгебраическая сумма количеств теплоты, сообщаемых на всех участках этого процесса. В ходе процесса теплота может поступать в систему или уходить из неё разными способами.При отсутствии работы над системой и потоков энергии-вещества, когда
— это алгебраическая сумма количеств теплоты, сообщаемых на всех участках этого процесса. В ходе процесса теплота может поступать в систему или уходить из неё разными способами.При отсутствии работы над системой и потоков энергии-вещества, когда  ,
,  ,
,  , выполнение системой работы
, выполнение системой работы 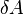 приводит к тому, что
приводит к тому, что 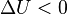 , и энергия системы
, и энергия системы 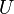 убывает. Поскольку запас внутренней энергии
убывает. Поскольку запас внутренней энергии 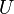 ограничен, то процесс, в котором система бесконечно долгое время выполняет работу без подвода энергии извне, невозможен, что запрещает существование вечных двигателей первого рода.
ограничен, то процесс, в котором система бесконечно долгое время выполняет работу без подвода энергии извне, невозможен, что запрещает существование вечных двигателей первого рода.
Первое начало термодинамики:
· при изобарном процессе
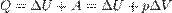
при изохорном процессе (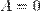 )
)
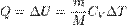
при изотермическом процессе 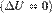
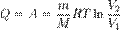
Здесь 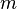 — масса газа,
— масса газа,  — молярная масса газа,
— молярная масса газа,  — молярная теплоёмкость при постоянном объёме,
— молярная теплоёмкость при постоянном объёме, 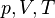 — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.
— давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.
| Применение первого закона термодинамики к идеальному газу |
20. Первый закон термодинамики позволяет вычислить изменение параметров идеального газа при тепловых и механических процессах.
Так, если в газе протекают изопроцессы, первый закон термодинамики может быть записан в частном виде.
При изотермическом процессе изменения внутренней энергии в идеальном газе не происходит и все подводимое к газу количество теплоты идет на совершение им работы.
|
При изохорном процессе объем газа остается постоянным. Соответственно, не совершается работа и внутренняя энергия газа изменяется исключительно за счет теплообмена с окружающей средой.
|
(Индекс V означает, что процесс протекает при постоянном объеме).
Если при теплообмене происходит изменение температуры газа на Δ T, то QV = cVm Δ T.
cV – удельная теплоемкость газа при постоянном объеме.
Подставляя это выражение в уравнение первого закона термодинамики для изохорного процесса, имеем: Δ U = cVm Δ T.
С другой стороны, для одноатомного идеального газа 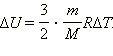
Приравняв правые части уравнений и произведя соответствующие преобразования, имеем: 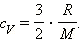
При изобарном процессе изменение внутренней энергии газа происходит как за счет теплообмена, так и за счет совершения механической работы. Если к газу подводится некоторое количество теплоты, то оно частично расходуется на увеличение внутренней энергии газа, частично на совершение газом работы при его расширении.
|
(Индекс p означает, что процесс протекает при постоянном давлении).Давление газа остается постоянным за счет соответствующего изменения объема. Так как Δ U = QV, то Qp = QV + p Δ V. Таким образом оказывается, что для повышения температуры газа на одно и то же количество градусов при постоянном давлении надо сообщить ему большее количество теплоты, чем при постоянном объеме, так часть теплоты расходуется на совершение работы.Если обозначить удельную теплоемкость при постоянном давлении cp, то первый закон термодинамики для изобарного процесса примет вид: 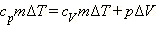 или:
или: 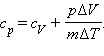
Из уравнения Менделеева–Клапейрона следует, что 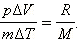
Таким образом, 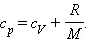
С учетом того, что 
Наряду с удельными теплоемкостями газа при постоянном объеме и постоянном давлении cV и cp, можно ввести молярные теплоемкости CV = cVM при постоянном объеме и Cp = cpM при постоянном давлении. Сделав это, имеем: Cp = CV + R. Полученное уравнение носит название уравнения Майера.Кроме рассмотренных, возможен еще вариант, когда термодинамическая система не обменивается теплотой с окружающей средой. Процесс, происходящий при этом с газом, называется адиабатным. При адиабатном процессе работа совершается газом за счет убыли его внутренней энергии, либо наоборот, за счет совершения над газом работы, увеличивается его внутренняя энергия. Q = 0; A = –Δ U.

|
Адиабатный процесс и его результаты можно пронаблюдать с помощью следующих опытов. Бутылку из светлого стекла закрепим в штативе и закроем пробкой, сквозь которую пропущена трубка. На трубку надет шланг, соединенный с нагнетающим насосом. Будем увеличивать давление воздуха в бутылке до тех пор, пока из нее не будет выбита пробка. Газ, расширяясь, совершает работу. В результате этого его внутренняя энергия уменьшается, соответственно, падает и температура. Об уменьшении температуры газа можно судить по появлению в сосуде тумана.

|
Насыпем в запаянный с одного конца прозрачный цилиндр легковоспламеняющееся вещество. В качестве такого вещества используется одна раздавленная в пыль головка от спички. Вставим в цилиндр поршень. При резком сжатии газа, находящегося в цилиндре, его внутренняя энергия повышается, соответственно, повышается и температура. Это приводит к воспламенению горючего вещества.
Среди равновесных процессов, которые происходят с термодинамическими системами, отдельно рассматриваются изопроцессы, при которых один из основных параметров состояния остается постоянным. Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.

Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:

т.к.CV=dUm/dt,

Тогда для произвольной массы газа получим
 (1)
(1)
Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна
 (2)
(2)
и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то
 и
и 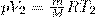
откуда
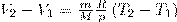
Тогда выражение (2) для работы изобарного расширения примет вид
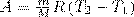 (3)
(3)
Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 —T1 = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.
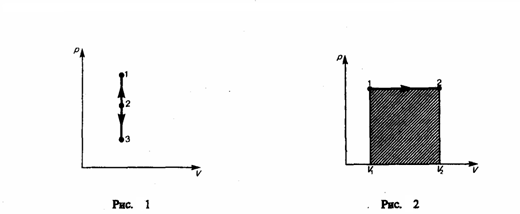
Рис.1
В изобарном процессе при сообщении газу массой m количества теплоты
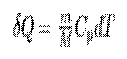
его внутренняя энергия возрастает на величину (т.к. CV=dUm/dt)

При этом газ совершит работу, определяемую выражением (3).
Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:
 Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа:
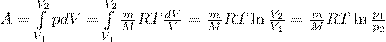
Так как при Т=const внутренняя энергия идеального газа не изменяется:
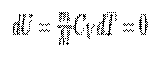
то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса

т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
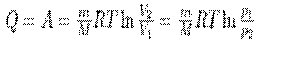 (4)
(4)
Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения.
21. Теплоёмкостью системы называется количество тепла, которое необходимо сообщить системе, чтобы температура её увеличилась на 1o. Если под системой понимается 1 моль вещества, то теплоёмкость называется молярной и обозначается C. Если под системой понимается единица массы вещества, то теплоёмкость называется удельной и обозначается Суд. Здесь m – масса; M – молярная масса; Cm – теплоёмкость системы массы m.Введение теплоёмкости и особенно молярной и удельной теплоёмкостей позволяет при сходных условиях сравнивать системы из разного вещества и разной структуры. Теплоёмкость характеризует процесс. Можно указать разные процессы, приводящие к одному и тому же изменению температуры, но при каждом из них системе сообщается разное количество тепла. Таким образом, с помощью I закона термодинамики и уравнения состояния идеального газа удалось получить полезную формулу, выражающую соотношение между теплоёмкостями Cp и СV (оно называется соотношением Майера). Изотермический процесс с идеальным газом. Для этого процесса T = const, dT = 0. Изменение внутренней энергии (функции только температуры) равно нулю. 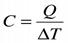 Значит, по I закону термодинамики. Сообщённая газу теплота идёт на совершение им работы. Это самый подходящий процесс для тепловой машины (если не замечать трудностей обеспечивания многократной повторяемости процесса). Ещё одним замечательным процессом является адиабатический процесс – процесс без теплообмена с окружающей средой. На практике адиабатическими можно считать такие процессы, когда за характерное время процесса система не успевает получить заметное количество тепла (по сравнению, например, с работой). Критерий отсутствия теплообмена должен учитывать и теплоизоляционные качества стенок и быстроту протекания процесса. Даже в случае, казалось бы, плохих теплоизоляционных характеристик стенок процесс является адиабатическим, если протекает достаточно быстро.Примерами адиабатического процесса являются: быстрое расширение газа при кратковременном вытекании некоторой порции его через малое отверстие; быстрое сжатие горючей смеси в цилиндре двигателя внутреннего сгорания; периодические сжатия и расширения вещества в поле звуковой волны.Быстрые адиабатические процессы могут считаться квазистатическими, если при сравнительно малых экстенсивных параметрах системы время релаксационных процессов в ней пренебрежимо мало по сравнению с характерным временем процесса.
Значит, по I закону термодинамики. Сообщённая газу теплота идёт на совершение им работы. Это самый подходящий процесс для тепловой машины (если не замечать трудностей обеспечивания многократной повторяемости процесса). Ещё одним замечательным процессом является адиабатический процесс – процесс без теплообмена с окружающей средой. На практике адиабатическими можно считать такие процессы, когда за характерное время процесса система не успевает получить заметное количество тепла (по сравнению, например, с работой). Критерий отсутствия теплообмена должен учитывать и теплоизоляционные качества стенок и быстроту протекания процесса. Даже в случае, казалось бы, плохих теплоизоляционных характеристик стенок процесс является адиабатическим, если протекает достаточно быстро.Примерами адиабатического процесса являются: быстрое расширение газа при кратковременном вытекании некоторой порции его через малое отверстие; быстрое сжатие горючей смеси в цилиндре двигателя внутреннего сгорания; периодические сжатия и расширения вещества в поле звуковой волны.Быстрые адиабатические процессы могут считаться квазистатическими, если при сравнительно малых экстенсивных параметрах системы время релаксационных процессов в ней пренебрежимо мало по сравнению с характерным временем процесса.
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
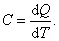
| (4.2.1) |
Размерность теплоемкости: [ C ] = Дж/К.
Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [ Cуд ] = Дж/К.
Для газов удобно пользоваться молярной теплоемкостью Cμ - количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
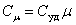
| (4.2.2) |
[Cμ] = Дж/(моль×К).
Из п. 1.2 известно, что молярная масса – масса одного моля:

|
где А – атомная масса; mед - атомная единица массы; NА - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода 12С. Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV.
СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).
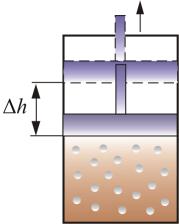
Рис. 4.2
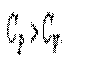 Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что
Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что
Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния. Величины СР и СV оказываются связанными простыми соотношениями. Найдём их. Пусть мы нагреваем один моль идеального газа при постоянном объёме(d A = 0). Тогда первое начало термодинамики запишем в виде:
 , ,
| (4.2.3) |
т.е. бесконечно малое приращение количества теплоты 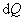 равно приращению внутренней энергии d U.
равно приращению внутренней энергии d U.
Теплоемкость при постоянном объёме будет равна:
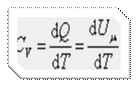 , ,
| (4.2.4) |
В общем случае
 , ,
|
так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4).
Из (4.2.4) следует, что 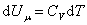
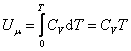 , ,
|
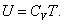 , ,
| (4.2.5) |
Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.
Для произвольной идеальной массы газа:
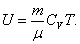 , ,
| (4.2.6) |
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
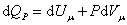 . .
|
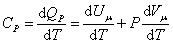 . .
| (4.2.7) |
Из основного уравнения молекулярно-кинетической теории  . При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:
. При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:
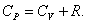 . .
| (4.2.8) |
Это уравнение Майера для одного моля газа. Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж. Полезно знать формулу Майера для удельных теплоёмкостей:
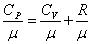 . .
|
или
 . .
| (4.2.9) | |||
22. Закон Максвелла о распределении по скоростям и энергиям Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от v до v + dv. Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале v ÷ v + dv к общему числу молекул N и величине интервала dv
Максвелл использовал два предложения: а) все направления в пространстве равноправны и поэтому любое направление движения частицы, т.е. любое направление скорости одинаково вероятно. Это свойство иногда называют свойством изотропности функции распределения. б) движение по трем взаимно перпендикулярным осям независимы т.е. х-компоненты скорости Считается также, что газ состоит из очень большого числа N тождественных молекул находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Силовые поля на газ не действуют. Функции f (v) определяет относительное число молекул dN(v)/N скорости которых лежат в интервале от v до v + dv (например: газ имеет N = 106 молекул, при этом dN = 100 молекул имеют скорости от v =100 до v + dv =101 м/с (dv = 1 м Используя методы теории вероятностей, Максвелл нашел функцию f (v) - закон распределения молекул идеального газа по скоростям:
f (v) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т) f(v) зависит от отношения кинетической энергии молекулы, отвечающей рассматриваемой скорости
<X>= Тогда средняя арифметическая скорость молекул
и интегрируя по частям получили
Скорости, характеризующие состояние газа
|
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 1864; Нарушение авторских прав?; Мы поможем в написании вашей работы!
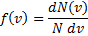
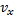 не зависит от того каково значения ее компонент
не зависит от того каково значения ее компонент  или
или 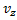 . И тогда вывод f (v) делается сначала для одной компоненты
. И тогда вывод f (v) делается сначала для одной компоненты 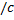 ) тогда
) тогда  .
.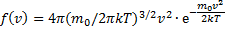
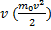 к величине kT характеризующей среднюю тепловую энергию молекул газа.
к величине kT характеризующей среднюю тепловую энергию молекул газа.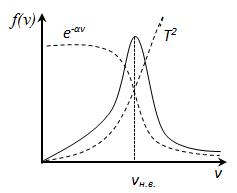 При малых v
При малых v 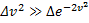 и функция f(v) изменяется практически по параболе
и функция f(v) изменяется практически по параболе 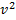 . При возрастании v множитель
. При возрастании v множитель 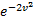 уменьшается быстрее, чем растет множитель
уменьшается быстрее, чем растет множитель 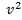 , т.е. имеется max функции f(v). Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью
, т.е. имеется max функции f(v). Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью  найдем из условия
найдем из условия

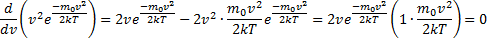

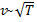 , следовательно, с ростом температуры наиболее вероятная скорость растёт, но площадь S, ограниченная кривой функции распределения остаётся неизменной, так как из условия нормировки
, следовательно, с ростом температуры наиболее вероятная скорость растёт, но площадь S, ограниченная кривой функции распределения остаётся неизменной, так как из условия нормировки 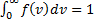 (так как вероятность достоверного события равна 1), поэтому при повышении температуры кривая распределения f (v) будет растягиваться и понижаться.
(так как вероятность достоверного события равна 1), поэтому при повышении температуры кривая распределения f (v) будет растягиваться и понижаться.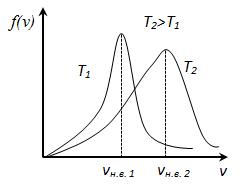 В статистической физике среднее значение какой-либо величины определяется как интеграл от 0 до бесконечности произведения величины на плотность вероятности этой величины (статистический вес)
В статистической физике среднее значение какой-либо величины определяется как интеграл от 0 до бесконечности произведения величины на плотность вероятности этой величины (статистический вес)