Электропроводность

Для описания электропроводности необходимо знать связь между плотностью тока и полем 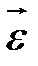, вызывающим этот ток. При наличии в полупроводнике носителей заряда двух сортов — электронов и дырок — для плотности тока получаем:

(1.4)

где и 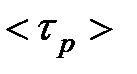— усредненные по энергии времена релаксации электронов и дырок, соответственно, и 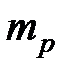— эффективные массы носителей заряда, — электропроводность, п и р — концентрации электронов и дырок.

Из (1.4) видно, что

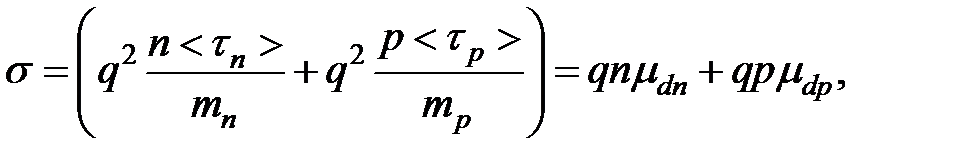(1.5)

где 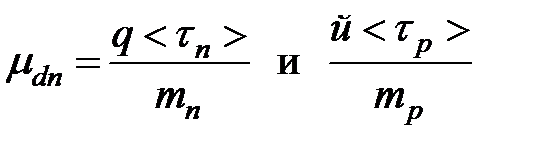— дрейфовые подвижности электронов и дырок соответственно. Дрейфовая подвижность численно равна скорости дрейфа в электрическом поле единичной напряженно­сти.

Из (1.5) следует, что температурная зависимость проводимости опре­деляется зависимостями п(Т) и 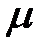(Т).

Рассмотрим температурную зависимость концентрации носителей заряда.

Концентрация электронов в с-зоне может быть найдена следующим образом:

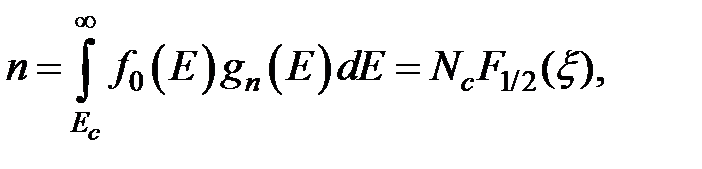(1.6)

где 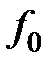— равновесная функция распределения, 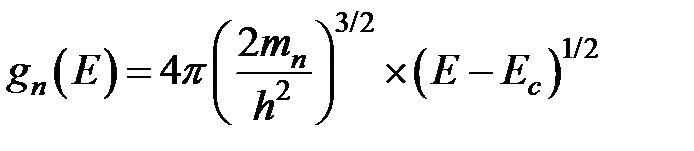— плотность состояний в с-зоне для параболической зоны; 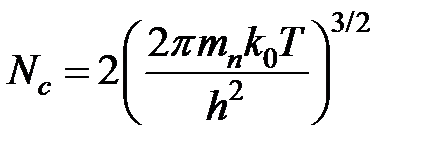— эффективная плотность состояний в с-зоне; 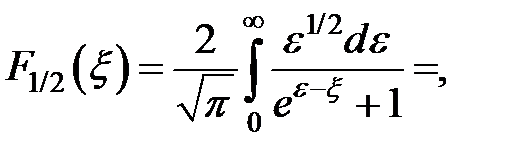— интеграл Ферми с индексом 1/2.

Для невырожденного электронного газа

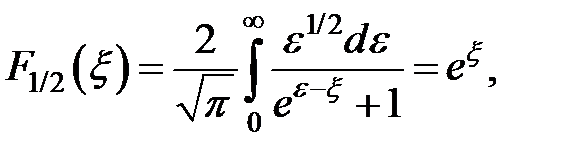(1.7)

Где 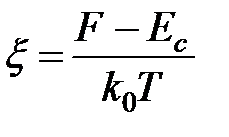− приведенный Уровень Ферми.

Тогда

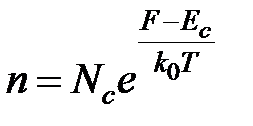(1.8)

Аналогично, для концентрации дырок в отсутствии вырождения лег­ко получить,

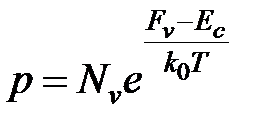(1.9)

Где 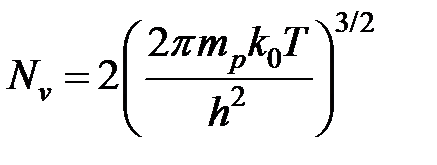— эффективная плотность состояний в v -зоне.

Для нахождения уровня Ферми используется условие электроней­тральности, по которому суммарный заряд всех заряженных частиц кристалла должен быть равен нулю:

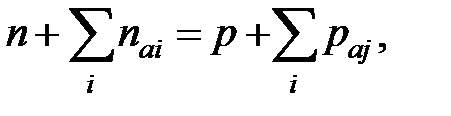(1.10)

где 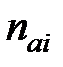— число электронов на i -ом акцепторном уровне, — число дырок на j -ом донорном уровне.

Рассмотрим, например, полупроводник, содержащий один сорт до-норной примеси с концентрацией уровень которой расположен на расстоянии ниже дна зоны проводимости 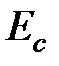Решая уравнение электронейтральности для этого случая, получаем следующий результат.

В области низких температур, когда уровень Ферми находится выше донорного уровня, концентрация электронов в с-зоне при увеличении температуры растет за счет ионизации примесных центров:

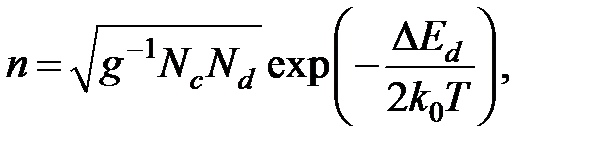(1.11)

где g — фактор спинового вырождения.

В области средних температур, когда уровень Ферми находится ниже донорного уровня, концентрация электронов в с-зоне остается постоян­ной, так как примесь вся ионизована, а ионизация собственных атомов еще не существенна:

(1.12)

Наконец, в области высоких температур происходит ионизация соб­ственных атомов полупроводника и

(1.13)

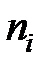принято называть собственной концентрацией носителей заряда.

На рис. 1.1 приведена температурная зависимость концентрации носи­телей заряда для нескольких образцов с разной концентрацией примеси 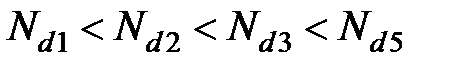. Поскольку в двух температурных областях зависимость п(Т) носит экспоненциальный характер, эти кривые приня­то строить в спрямляющих координатах . Это дает воз­можность определить энергию ионизации примеси 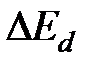при низких и ширину запрещенной зоны при высоких температурах. Действи­тельно,

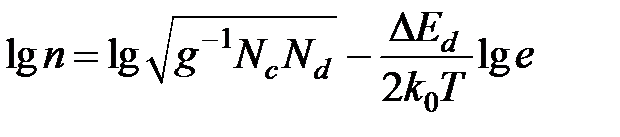(1.14)

и

.

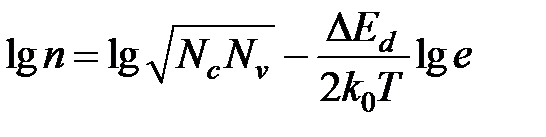Тогда 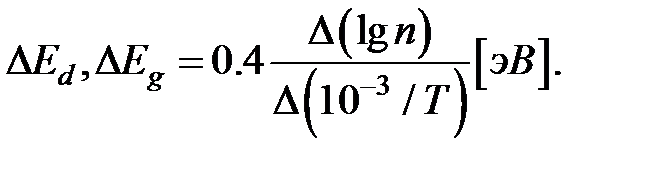(1.15)

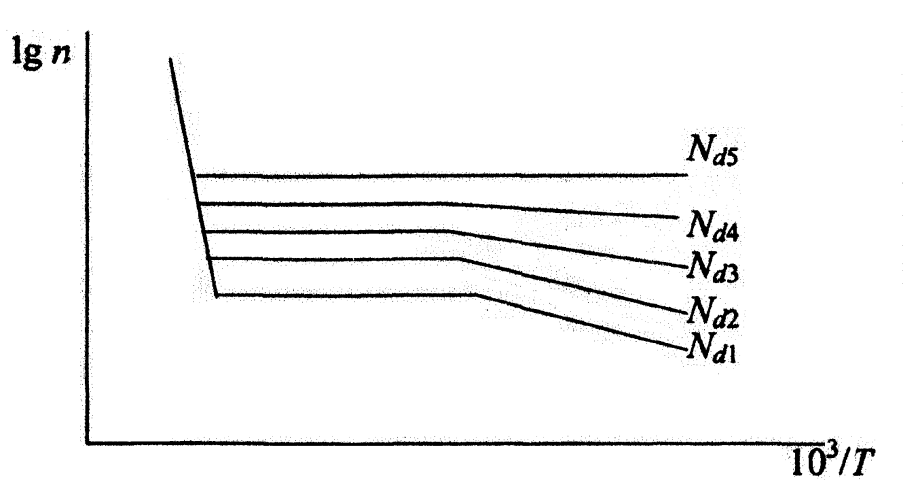
Рисунок 1.1 − Зависимость концентрации электронов от температуры

Для более точного определения энергии, особенно энергии иониза­ции примеси, следует учесть температурную зависимость предэкспоненциального множителя и строить зависимость п(Т) в координатах

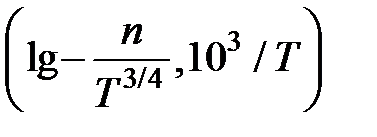при низких температурах 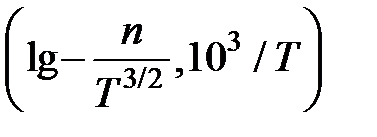и при
высоких температурах.

Уменьшение наклона прямой при возрастании концентрации приме­си при низких температурах обусловлено тем, что при достаточно высо­кой концентрации примеси дискретный примесный уровень размывает­ся в зону и расстояние от верхнего уровня этой зоны до 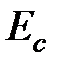уменьшается. Переход к нулевому наклону свидетельствует о слиянии примесной зоны с зоной проводимости. Это означает вырождение электронного газа в полупроводнике.

Температурная зависимость подвижности определяется, очевидно, температурной зависимостью времени релаксации, которая, в свою оче­редь, зависит от конкретного механизма рассеяния носителей заряда. Наиболее часто реализуются два вида рассеяния: на тепловых колебани­ях решетки (для атомных полупроводников — на акустических) и на ионизованной примеси. Теоретическое рассмотрение дает зависимость

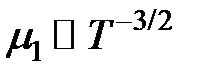для рассеяния на акустических колебаниях решетки и

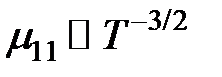для рассеяния на ионизованной примеси. Если в кристалле действуют оба механизма рассеяния, то

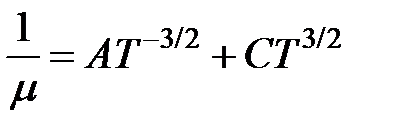, (1.16)

где А и С — не зависящие от температуры величины. На рис.1.2 приведена температурная зависимость подвижности, полученная при этих предположениях. При низких температурах доминирует примесное рассеяние, при высоких — тепловое.

При увеличении концентрации примеси подвижность становится меньше в той области температур, где доминирует рассеяние на ионах примеси.

Перейдем к рассмотрению температурной зависимости электропро­водности. Видно, что в любом случае зависимость подвижности от тем­пературы носит степенной характер. Поэтому из сравнения температур­ных зависимостей концентрации и подвижности следует, что характер зависимости 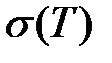определяется подвижностью лишь в том случае, если концентрация носителей заряда не зависит от температуры (в области насыщенной примесной проводимости). В области же низких и высоких температур, где концентрация экспоненциально меняется с температу­рой, именно она определяет температурную зависимость электропро­водности (рис. 1.3).

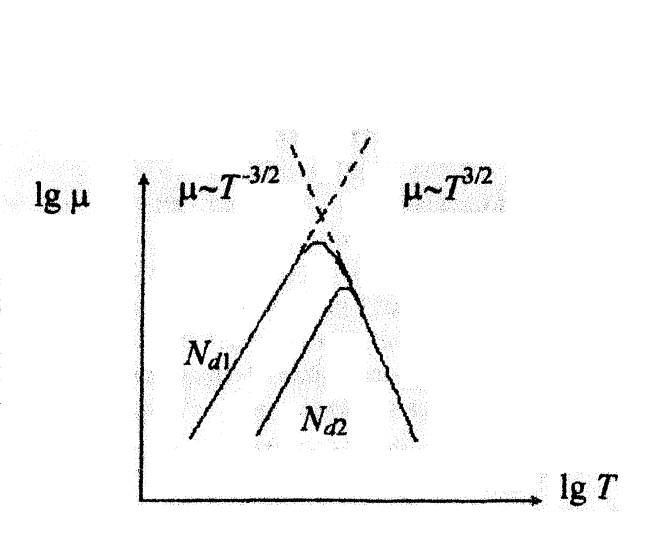
Рисунок 1.2 − Температурная зависимость подвижности носителей зарядов при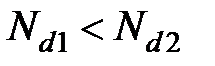

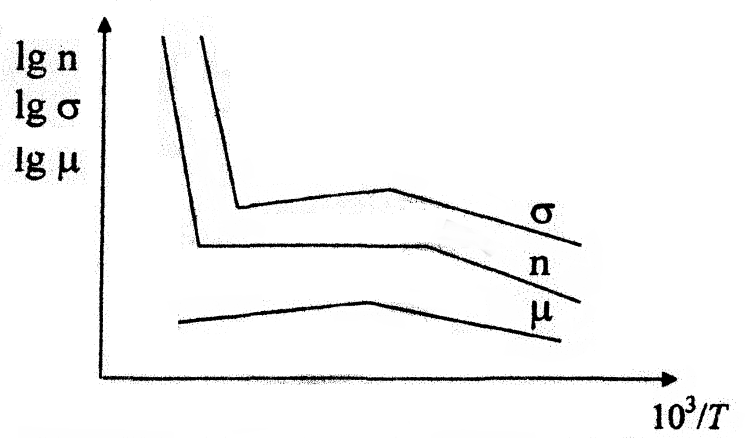
Рисунок 1.3 − Зависимость концентрации и подвижности носителей заряда и проводимости от температуры

Экспоненциальная зависимость 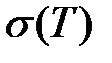позволяет определять 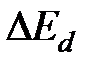в области низких температур и 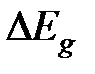в области собственной проводимости аналогично тому, как эти величины определяются из температурной зависимости концентрации (см. формулу (1.15)). Отметим, что ввиду ма­лых значений 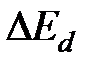при определении этой величины желательно учиты­вать температурные зависимости подвижности и предэкспоненциального множителя в выражении для концентрации.

Дата добавления: 2014-11-20