Эффект Холла в слабых магнитных полях

Рассмотрим однородный изотропный полупроводник в форме параллелепипеда с концентрацией электронов n (концентрация дырок пренебрежимо мала). Через него течет электрический ток с плотностью 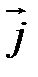. Поместим наш образец в однородное магнитное поле, вектор магнитной индукции 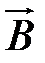перпендикулярен вектору 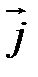(см. рис. 2.1). На электроны, дрейфующие в электрическом поле со скоростью 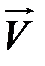будет действо­вать сила Лоренца Поэтому дрейф электронов будет иметь составляющую не только по оси “X” но и по оси “Z”. Это приве­дет к накоплению электронов на нижней грани образца, а на верхней будет их "дефицит"; в результате появится электрическое поле направ­ленное вдоль оси “Z”. Дрейф электронов вдоль оси “Z” будет продол­жаться до тех пор, пока возникшее электрическое поле не уравновесит силу Лоренца.

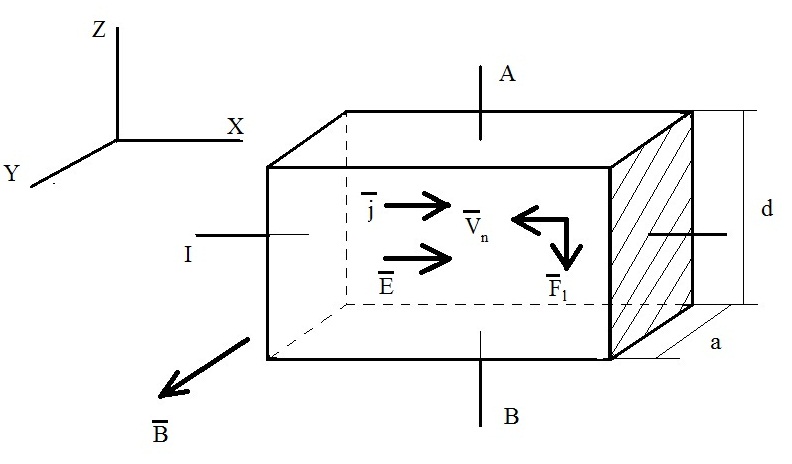
Рисунок 2.5 − Направление векторов в полупроводниковом образце л-типа при измерении эффекта Холла

Сделаем теперь количественное описание данного явления. Уравне­ние движения электрона в скрещенных электрическом и магнитном по­лях имеет вид:

(2.1)

или в скалярной форме (направления векторов показаны на рис. 2.1):

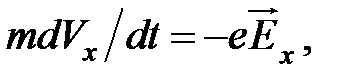(2.2а)

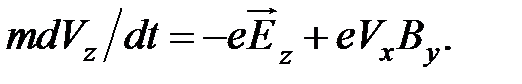(2.2б)

Поскольку сила Лоренца скомпенсирована силой, действующей на электрон со стороны электрического поля вдоль оси "Z", то уравнение (2.2б) будет иметь вид:

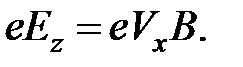(2.3)

Проинтегрировав (2.2a), получим:

(2.4)

Но электрон в кристалле не может двигаться бесконечно долго без столкновений. Можно показать, что ансамбль электронов в кристалле при определенной температуре будет иметь среднее время свободного пробега 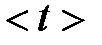, его принято называть временем релаксации и обозна­чать греческой буквой . Поскольку нас интересует средняя скорость Дрейфа, то вместо (2.4) можем записать:

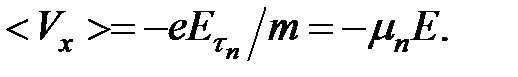(2.5)

Величину 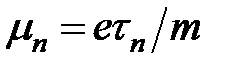называют подвижностью носителей заряда; подстрочные индексы "n" или "p" указывают на то, что данная величи­на относится к электронам или дыркам соответственно. Из уравнения (2.5) подвижность можно определить как скорость дрейфа носителей заряда в электрическом поле единичной напряженности.

Запишем плотность электрического тока в виде:

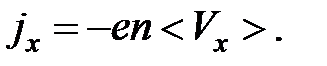(2.6)

Подставив (2.5) в (2.6), получим:

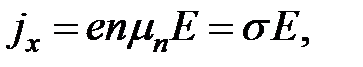(2.7)

Где — проводимость полупроводника. Выражение (2.7) есть не что иное, как известный закон Ома.

Рассмотрим теперь уравнение (2.3). Из него мы можем определить на­пряженность электрического поля вдоль оси "Z". Используя (2.6), вместо (2.3) получим:

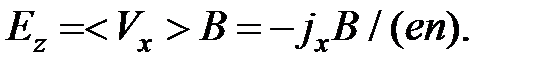(2.8)

Величина называется полем Холла. Таким образом, электрическое поле (для нашей ориентации векторов) имеет компоненты 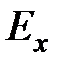и cледовательно, полный вектор электрического поля

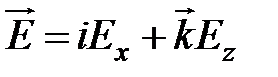
уже не будет совпадать по величине и направлению с первоначальным,

когда ; между ними будет угол 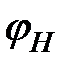, получивший название "угол Холла". Для тангенса этого угла можно записать:

или

(2.9)

На практике удобнее измерять не напряженность электрического по­ля, а соответствующую разность потенциалов (между точками А и В на рис.2.1), которая называется ЭДС Холла:

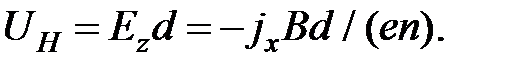(2.10)

Если выразить плотность тока через полный ток, протекающий в образце

то получим

(2.11)

где 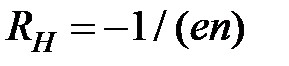— постоянная Холла.

В случае полупроводника р -типа проводимости в уравнении (2.1) следует изменить знак носителей заряда с “ ”на “ 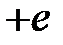”. Выполнив такие же преобразования, как и для полупроводника n -типа, вместо формул(2.7), (2.8), (2.9), (2.11) будем иметь:

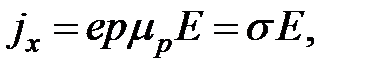(2.12)

(2.13)

(2.14)

(2.15)

где р — концентрация дырок, 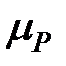— их подвижность − постоянная Холла для дырочного полупроводника. Сопоставляя (2.11) и (2.15), можно видеть, что по знаку ЭДС Холла можно определить э эксперименте тип носителей заряда, а по величине 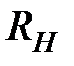− их концентрацию. Кроме того, если возможно измерение и проводимости, и постоянной Холла, то по ним определяют подвижность носителей:

(2.16)

Теперь рассмотрим ситуацию, когда в полупроводнике есть и электроны, и дырки. Вместо уравнения (2.1) имеем два уравнения:

— для электронов,

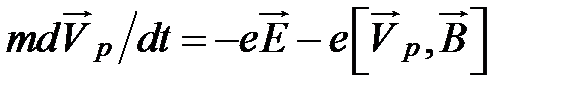—для дырок. (2.17)

Проинтегрировав уравнения (2.17), используя определение подвижности, получим:

(2.18)

Домножив первое уравнение на “ ” а второе на “ ”, получим уравнения для электронного и дырочного токов:

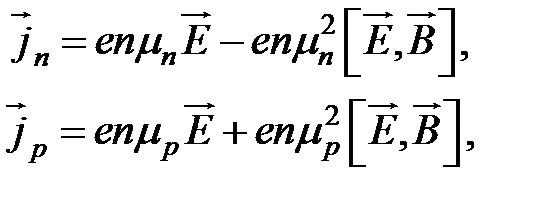(2.19)

Таким образом, полный ток:

(2.20)

или в скалярной форме:

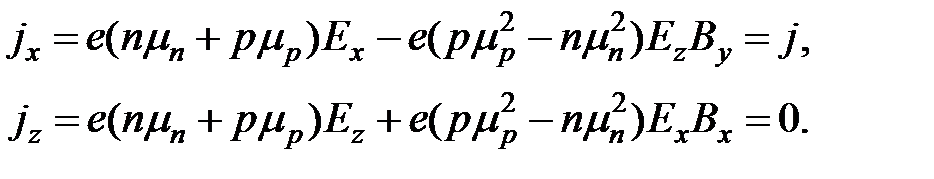(2.21)

Поскольку магнитное поле слабое, то второе слагаемое в первом уравнении системы (2.21) много меньше первого. С учетом этого, решив систему (2.21) относительно 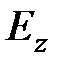, получим:

(2.22)

Из (22) видно, что при n>>p 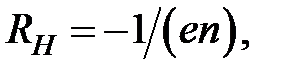, а при р>>n . В случае собственного полупроводника, где

(2.23)

где . Согласно (2.23), 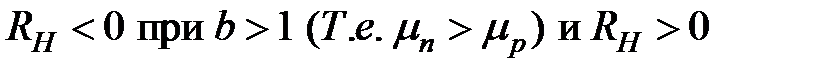при .

Выше мы полагали, что все носители заряда имеют одно и то же время релаксации, иными словами — мы считали вероятность рассеяния не зависящей от скорости движения. При строгом рассмотрении необ­ходимо учитывать распределение носителей по скоростям; следствием этого будет зависимость времени релаксации электронов (дырок) от их кинетической энергии. Описание кинетических явлений в ансамбле час­тиц при учете их распределения по энергии обычно выполняют с помо­щью кинетического уравнения Больцмана:

(2.24)

здесь: — энергия электрона (дырки) в зависимости от волнового вектора — функция распределения в момент времени , — функция распределения в момент времени , — скорость носителя заряда, 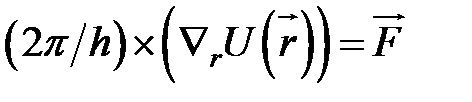— сила, обусловленная внешними макроскопическими полями 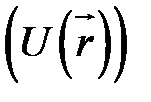— потенциальная энергия носителя заряда в этих внешних полях), 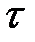— время релаксации. Уравнение Больцмана позволяет найти стационарную функцию распределения, если известны структура энергетических зон и внешние поля. Следствием рассмотрения эффекта Холла с помощью этого уравнения будет появление множителя

в выражении для постоянной Холла:

— для электронов,

— для дырок, (2.25)

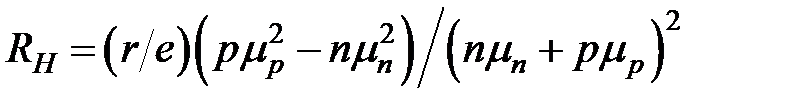— для биполярной проводимости.

Здесь — среднее время релаксации, 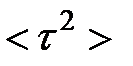— средний квадрат времени релаксации.

Соответственно, все полученные выше формулы, где есть множители или 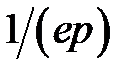верны с точностью до множителя r; в частности, для подвижности:

(2.26)

Поэтому подвижность, определяемую с помощью эффекта Холла, называют холловской, в отличие от истинной (дрейфовой). Множитель r получил название фактора Холла.

Поскольку r определяется временем релаксации 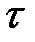, то его величина будет зависеть от механизмов рассеяния носителей заряда. Подсчитано, что при рассеянии на акустических колебаниях кристаллической решет­ки

а при рассеянии на примесных ионах

.

При низких температурах (для Ge Т < 250 К, для Si Т<100 К) обычно доминирует рассеяние носителей на ионах примесей, а при вы­соких температурах (для Ge и Si — в том числе и при комнатной тем­пературе) преобладает рассеяние на колебаниях решетки.

Если в кристалле преобладают упругие механизмы рассеяния, то Холл-фактор имеет одинаковое значение для электронов и дырок.

Дата добавления: 2014-11-20