Определение параметров неосновных носителей заряда в полупроводниках

Модифицированный метод Ван-дер-Пау (для планарного размещения зондов)

При измерении эффекта Холла методом Ван-дер-Пау в тонких полупроводниковых слоях возникают трудности с установкой зондов. В свя­зи с этим данный метод был модифицирован так, чтобы было возможно планарное размещение контактов, т. е. на поверхности исследуемого слоя или образца (один из таких вариантов для образца в форме парал­лелепипеда приведен на рис. 2.4 и используется в настоящей работе).

При измерении проводимости ток подводится через зонды 1 и 4, а разность потенциалов измеряют между зондами 2 и 3. Проводимость для этой конфигурации контактов подсчитывают по формуле:

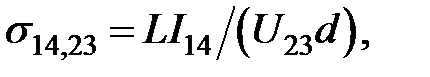(2.41)

где L — поправочный множитель, учитывающий геометрию образца (см. табл. 2.2). Затем геометрию измерений меняют: через зонды 1 и 2 пропускают ток, а между другой парой (3 и 4) определяют падение на­пряжения. Из полученных данных находят . Истинную проводи­мость 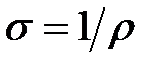находят по формуле:

(2.42)

При определении постоянной Холла ток I подводится через зонды 1 и 3, между другой парой контактов (2 и 4) измеряют падение напряже­ния. Для этой конфигурации контактов постоянная Холла равна:

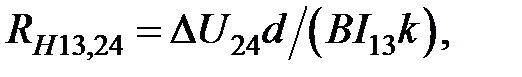(2.43)

Где 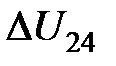— изменение напряжения между зондами 2 и 4 после вклю­чения магнитного поля, k — поправочный множитель, учитывающий геометрию образца и конфигурацию зондов (см. табл. 2.2). Затем повто­ряют измерения, изменив назначение контактов: через 2 и 4 подают ток 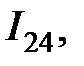а с 1 и 3 снимают разность напряжений 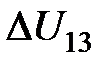. По этим данным определяют 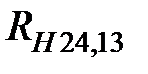. Истинная постоянная Холла находится как сред­нее арифметическое :

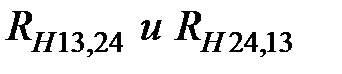(2.44)

При электрических измерениях на полупроводниковых образцах обычно сталкиваются с проблемой учета контактной разности потен­циалов и других паразитных ЭДС. Точный расчет поправок возможен здесь лишь для простейших случаев. Для исключения (или значительно­го уменьшения) вклада контактных потенциалов в измеряемые напря­жения до недавнего времени применяли компенсационные методы из­мерений (к измерительным зондам подключался внешний источник на­пряжения так, чтобы полностью компенсировать измеряемую разность потенциалов). Последнее время для этих целей используют электромет­рические цифровые вольтметры (входное сопротивление 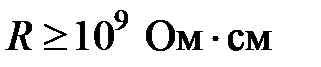). В обоих случаях создаются условия, когда можно пренебречь протеканием тока через зонды, между которыми измеряется напряжение, и, следовательно, пренебречь падением напряжения на контактах. Ошибки, связанные с медленно меняющимися во времени помехами, удается значительно уменьшить, если проводить измерения при разных направлениях тока. В ошибку при определении постоянной Холла дает вклад и несимметричное размещение зондов. Исключить его можно, выполняя измерения при двух (противоположных) направлениях магнитного поля. Таким образом, для точного определения проводимо­сти и постоянной Холла при каждом значении тока необходимо сделать четыре измерения для 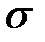и восемь для , а полученные данные усред­нить.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем состоит суть явления, получившего название "эффект Холла"? Какие величины характеризуют этот эффект?

2. Что означают термины сильное магнитное поле, слабое магнитное поле?

3. Используя уравнения движения для носителей заряда, получите связь между током, протекающим через образец, и ЭДС Холла.

4. Подсчитайте величину падения напряжения в результате протекания тока через образец германия n - или p -типа проводимости и ЭДС Холла, сравните их (численные значения тока, магнитной индукции, концентрации носителей и их подвижности задает преподаватель). Форма образца — куб с ребром 1 см, расположение контактов и ори­ентация векторов 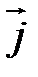и 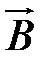такие же, как на рис.2.1.

5. Каким образом механизмы рассеяния влияют на величину постоян­ной Холла?

6. Используя уравнения движения для носителей заряда, покажите, что в случае биполярной проводимости при наличии магнитного поля и электроны, и дырки будут накапливаться на одной и той же грани образца. Выведите формулу для постоянной Холла в случае бипо­лярной проводимости.

7. Качественно нарисуйте и объясните температурные зависимости по­стоянной Холла в области примесной и собственной проводимости в полупроводниках n- и p -типа проводимости.

8. Какие особенности имеет эффект Холла в классически сильных маг­нитных полях?

9. В чем заключается метод Ван-дер*Пау для измерения проводимости и постоянной Холла?

ЗАДАНИЯ

1. Измерьте проводимость полупроводниковых образцов при несколь­ких значениях тока (количество образцов определяет преподаватель).

2. Для тех же образцов при тех же значениях тока измерьте ЭДС Холла и определите постоянную Холла при нескольких значениях магнит­ной индукции. Покажите, что в пределах экспериментальной ошибки постоянная Холла не зависит от величины тока и магнитной индук­ции.

3. Из полученных данных определите концентрацию носителей, их тип и холловскую подвижность. Экспериментальное значение подвижно­сти сравните с известными в литературе.

4. Используя результаты данной работы и лабораторной работы "Температурная зависимость термоэдс в полупроводниках", определите для образца германия эффективную плотность состояний в зоне проводимости 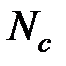при комнатной температуре (или в валентной зоне для

образца p -типа — 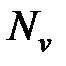) и эффективную массу электронов проводимости (дырок).

Литература

1. Ю.А. Байков, В.М. Кузнецов “Физика конденсированного состояния” М, Бином, 2011.

2. Г.И. Епифанов “Физика твёрдого тела” СП. б. Лань. 2009.

3. В.Л. Матухин, В.Л. Ермаков “ Физика твёрдого тела ” СП. б. Лань. 2009.

Целью работы является экспериментальное определение подвижно­сти, времени жизни и длины диффузии неосновных носителей заряда в германии.

Дата добавления: 2014-11-20