Измерения эффекта Холла и проводимости на образцах прямоугольной формы

Простейший способ одновременного измерения эффекта Холла и проводимости можно реализовать на полупроводниковых образцах прямоугольной формы. В этом случае контакты располагают, как показано на рис. 2.2. Контакты 1 и 2 служат для пропускания тока через образец, 3 и 4 — для измерения ЭДС Холла, 4 и 5 — для измерения проводимости (подобно тому, как это делается в четырехзондовом методе).

Для определения проводимости необходимо измерить величину тока, проходящего через образец, и падение напряжения 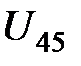между зондами 4 и 5. Тогда

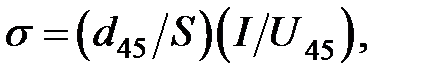(2.29)

где 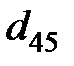− расстояние между контактами 4 и 5, S –площадь сечения образца.

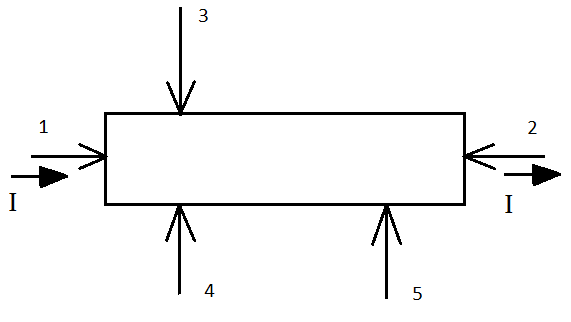
Рисунок 2. 2 − Размещение зондов на образце прямоугольной формы для измерений проводимости и ЭДС Холла

При измерении ЭДС Холла, необходимо учитывать вклады паразитных ЭДС, возникающих вследствие побочных гальваномагнитных и термомагнитных эффектов, а также из-за неэквипотенциальности кон­тактов 3 и 4 при нулевом магнитном поле. Напряжение между зондами 3 и 4 имеет следующие составляющие:

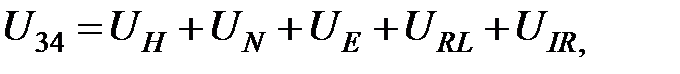(2.30)

где 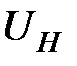− ЭДС Холла, 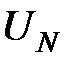− ЭДС Нернста, 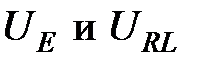термоэдс, возникающие благодаря эффектам Эттинсгаузена и Риги-Ледюка, 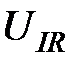— разность потенциалов, обусловленная неэквипотенциальностью контак­тов 3 и 4. Знак каждого из этих вкладов зависит от направления тока и магнитного поля. Для разных комбинаций направлений тока и поля бу­дем иметь:

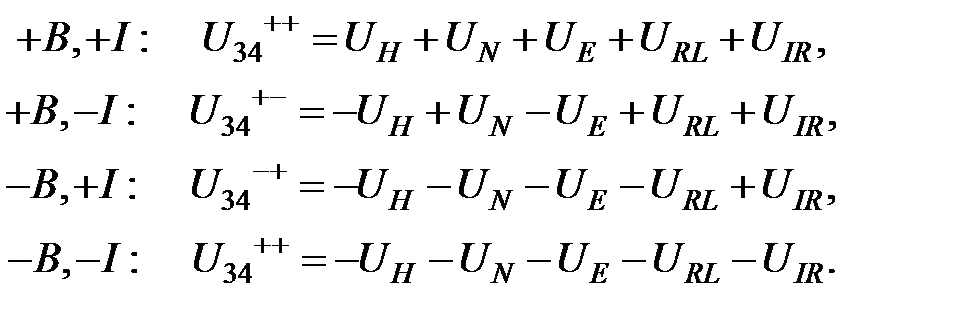(2.31)

Из уравнений (2.31) получаем:

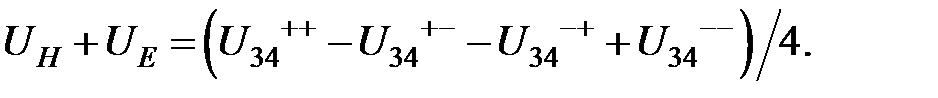(2.32)

Обычно 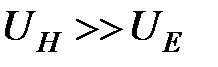, поэтому 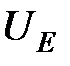можно пренебречь. Таким образом, для исключения побочных эффектов при каждом значении магнитного поля и тока нужно произвести измерения при 4 различных комбинациях направлений тока и магнитного поля. Для определения 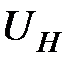полученные значения нужно брать с учетом знака. Теперь для постоянной Холла:

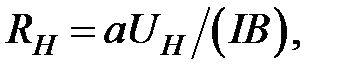(2.33)

а для холловской подвижности:

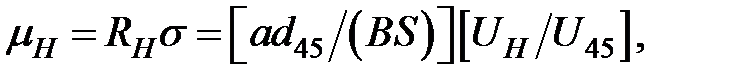
здесь а — толщина образца.

Дата добавления: 2014-11-20