Количество информации

Количеством информации называется степень уменьшения неопределенности после выбора (получения) сообщения в виде некоторого сигнала.

Например, если студент, первый подошедший к столу экзаменатора, тянет билет из 25 билетов, лежащих на столе, то вероятность p (возможность) того, что он вытащит билет с заданным номером равна 1/25 (одна возможность из 25), т.е. р = 1/25. После выбора билета неопределенности уже нет. Таким образом, число 25 можно было бы считать количеством информации, заложенным в одном выборе из 25 возможностей. Однако такое представление не является достаточно удобным, поскольку число возможностей в различных физических процессах может отличаться на много порядков. Р.Хартли предложил в качестве меры неопределенности логарифм от числа возможностей

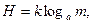
где k - коэффициент пропорциональности; m - число возможных выборов;

а - основание логарифма. При k = 1 и а = 2 стандартной единицей количества информации будет выбор их двух возможностей. Такая единица носит наименование бита и может быть представлена одним символом двоичного алфавита, обычно 0 или 1.

Количество информации определяется как разность неопределенности до получения сообщения и после. Если после получения сообщения неопределенность устраняется полностью, то формулы для определения количества информации и неопределенности совпадают.

Клод Шеннон обобщил формулу неопределенности на случай, когда Н зависит не только от m, но и от вероятностей выбора символов и вероятностей связи между ними.

Так, для количества сообщенной или индивидуальной информации он предложил соотношение

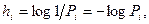
где Р_i - вероятность выбора i-го символа алфавита.

Удобнее в качестве количества информации пользоваться не значением h_i, а средним значением количества информации, приходящейся на один символ алфавита:

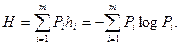
Для непрерывного сигнала эта формула приобретает вид:

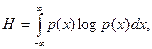
где p(x) - плотность распределения вероятности.

Контрольные задания

1.1. Дайте определение информатики как базовой учебной дисциплины.

1.2. Определите структуру дисциплины информатики и ее основные задачи.

1.3. Если область экрана имеет размеры 512x128 точек и каждая точка может иметь один из 256 оттенков, то каков минимальный объем памяти (Кбайт), необходимый для хранения этой области.

1.4. Дайте характеристику основных научных направлений, входящих в информатику.

1.5. Определить число бит, необходимых для записи числа 8¹².

1.6. Дайте определение понятия информации.

1.7. Сколько бит информации требуется для хранения в памяти ЭВМ слова ИНФОРМАТИКА?

1.8. Каковы формы представления информации?

1.9. Дайте определение понятия количества информации.

1.10. Приведите основные формулы для определения количества информации и поясните их смысл.

Глава 2. Компьютер как средство обработки информации

Дата добавления: 2014-11-20