Можно ли вращаться по инерции?

МАГИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Действительно, раскрутил карусель, – и вертись себе по инерции. Если подшипники карусели хорошие, то это можно делать достаточно долго. Современные маховики в накопителях энергии вращаются без помощи мотора более недели. Чем не вращение по инерции? Более того, если «помогать» этому маховику мотором, то он будет вращаться с совершенно постоянной угловой скоростью. Можно ли это назвать вращением по инерции?

Строго говоря, нет. Мы же раскритиковали Галилея, который именно движение точки по кругу считал инерционным. Но это потому, что на точку в этом случае должна обязательно действовать внешняя сила. А тогда движение уже не инерционное.

Поступим хитрее – возьмем много точек, расположенных по кругу, скрепим их друг с другом покрепче и раскрутим. Вот мы и получили маховик, который вращается, заметьте, без приложения внешних сил (мы его не трогаем!). Поместим такой маховик в космическое пространство – не понадобится ни подвес, ни мотор. Предмет сам собой вращается, никаких сил не требует.

Отвечайте, коллеги‑физики, – по инерции он движется или нет?

Вопрос, казалось бы, для школьника, но боюсь, что он станет проблемой и для специалиста‑физика.

Ответ первый:

– Да он вообще не движется, центр его масс, который находится на оси, неподвижен, стало быть, маховик неподвижен!

– Нет, – не согласимся мы, – а как же его кинетическая энергия? Может ли неподвижное тело обладать кинетической энергией и немалой?

Второй ответ:

– Это движение по инерции, потому что оно происходит без какого‑либо внешнего воздействия!

– Позвольте, – возразим мы, – но такое движение согласно первому закону Ньютона может быть только прямолинейным и равномерным. Может, Ньютон чего‑нибудь не учел?

Все учел Ньютон, просто вопрос не так уж тривиален, как может показаться сразу.

В чем различие между инерцией прямолинейного и вращательного движения?

Как известно, инерция, или инертность, массивной точки зависит только от ее массы. Масса является мерой инертности тела при прямолинейном движении. Значит, при таком движении на инерцию не влияет распределение масс в теле, и это тело можно смело принять за материальную (массивную) точку. Масса этой точки равна массе тела, а расположена она в центре тяжести, или, что почти то же, в центре масс, или центре инерции тела (поэтому «тело» в законах Ньютона справедливо заменено «материальной точкой»).

Проведем следующий опыт. Попытаемся вращать вокруг вертикальной оси стержень с насаженными на него массами (грузами), например, металлическими шарами. Пока эти шары находятся близ центра, раскрутить стержень легко, инертность его мала. Но если мы раздвинем массы на края стержня, то раскрутить такой стержень станет намного труднее, хотя масса его осталась без изменения (рис 52). Стало быть, инертность тела при вращении зависит не только от массы, но и (даже в большей степени) от распределения этих масс относительно оси вращения. Мерой инертности тела при вращении является так называемый момент инерции.

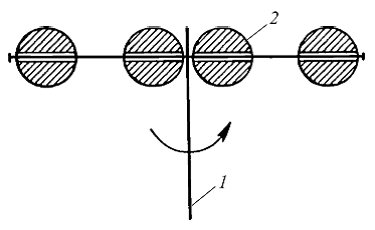
Рис. 52. Изменение момента инерции тела при неизменной его массе: 1 – стержень; 2 – груз

Моментом инерции тела относительно данной оси называется величина, равная сумме произведений масс всех частиц тела на квадраты их расстояний от этой оси.

Таким образом, разница в мере инертности прямолинейного движения и вращения состоит в том, что в первом случае она измеряется массой, а во втором – моментом инерции.

Далее. Как мы знаем, закон инерции устанавливает эквивалентность относительного покоя и равномерного прямолинейного движения – движения по инерции. Ибо нельзя никаким механическим опытом установить, покоится ли данное тело или движется равномерно и прямолинейно. Во вращательном движении это не так. Например, совсем не безразлично, покоится ли волчок или вращается равномерно, с постоянной угловой скоростью. Угловая скорость твердого тела является величиной, характеризующей его физическое состояние. Угловая скорость может быть определена (например, измерением центростремительных сил) без какой‑либо информации о положении тела по отношению к «абсолютной» системе координат. То есть если даже вся Вселенная исчезнет, а останется только наше вращающееся тело, то мы и в этом случае узнаем его угловую скорость. Поэтому термин «абсолютная угловая скорость тела» в отличие от «абсолютной скорости точки» должен употребляться в прямом смысле (без кавычек).

Таким образом, механические явления в покоящейся и вращающейся системах будут протекать по‑разному, не говоря уже о том, что падение и движение тел во вращающейся системе происходят иначе, чем в неподвижной: достаточно хорошенько ее раскрутить – и она развалится на части из‑за возникших в ней напряжений.

Поэтому второе отличие состоит в том, что прямолинейное движение и покой эквивалентны, а вращение, даже с постоянной угловой скоростью, может быть четко отделено не только от покоя, но и от вращения с другой угловой скоростью.

Вот, пожалуй, и все основные отличия. Остальное настолько одинаково, что можно взять на себя смелость сформулировать по образу и подобию ньютоновых законов «закон» инерции вращательного движения абсолютно твердого тела: «Изолированное от внешних моментов абсолютно твердое тело будет сохранять состояние покоя или равномерного вращения вокруг неподвижной точки или оси до тех пор, пока приложенные к телу моменты внешних сил не заставят его изменить это состояние».

Почему же абсолютно твердое тело, а не любое? Потому что у нетвердого тела из‑за вынужденных (или заранее предусмотренных) деформаций при вращении может измениться момент инерции, а это равносильно изменению массы тела в прямолинейном движении. Мы же не упоминаем этого случая, когда формулируем закон инерции, иначе он бы начинался так: «Изолированная от внешних воздействий материальная точка постоянной массы …» А эта точка может легко менять свою массу. Самолет или ракета, двигаясь за счет сжигания горючего, довольно существенно изменяют свою массу. Даже человек, пройдя достаточное расстояние, изменяет свою массу настолько, что это фиксируется медицинскими весами. А как отразится это изменение массы на инерции? Ведь при изменении массы возникает дополнительная, так называемая реактивная сила. О каком же движении по инерции может идти речь, когда на тело действует сила?

Так и в случае вращательного движения: если момент инерции непостоянен, приходится принимать постоянной не угловую скорость, а произведение угловой скорости на момент инерции – так называемый кинетический момент. В этом случае закон инерции примет такую форму: «Изолированное от внешних моментов относительно оси вращения тело будет сохранять кинетический момент относительно этой оси постоянным». Этот закон (в несколько иной формулировке) носит название закона сохранения кинетического момента.

Для демонстрации этого закона удобно воспользоваться простым прибором, называемым платформой (скамьей) Жуковского. Это круглая горизонтальная платформа на подшипниках, которая с малым трением может вращаться вокруг вертикальной оси (рис. 53). Если человек, стоя на этой платформе и вращаясь с некоторой угловой скоростью, разведет в сторону руки (еще лучше с грузами в них, например, гантелями), то его момент инерции относительно вертикальной оси повысится, а угловая скорость сильно упадет. Опуская руки, человек внутренним усилием сообщает себе первоначальную угловую скорость. Даже стоя на платформе неподвижно, можно повернуть корпус в любую сторону, вращая вытянутую вверх руку в противоположном направлении. Таким способом изменения угловой скорости широко пользуются в балете, акробатике и т. п., даже кошки успешно приземляются на лапы благодаря вращению хвоста в соответствующем направлении.

Рис. 53. Платформа Жуковского и человек

На явлении инерции вращательного движения основаны многочисленные приборы и машины, в частности, инерционные двигатели – аккумуляторы, сохраняющие кинетическую энергию при инерционном вращении маховика, и гироскопические приборы, сохраняющие, образно говоря, его кинетический момент. Существуют также и маховики переменного момента инерции, напоминающие по принципу действия человека на платформе Жуковского.

Дата добавления: 2014-11-20