III. Опрос учащихся по теоретическому материалу

II. решение задач.

1. Устно решить задачу № 933.

2. решить устно задачу № 943 по готовому чертежу на доске.

Решение

Из прямоугольного треугольника АОС по теореме Пифагора находим AC = 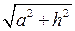; из прямоугольного треугольника ВОС находим по теореме Пифагора BC = .

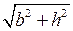3. Разобрать по учебнику и записать решение задачи № 953 в тетради (подчеркнуть, что теорема: «Сумма квадратов всех сторон параллелограмма, ромба, прямоугольника, квадрата равна сумме квадратов его диагоналей» – используется часто при решении задач по стереометрии в 10 и 11 классах) (рис. 283 учебника).

4. решить задачи №№ 991, 996, 997, 999 на доске и в тетрадях.

Примерные варианты карточек для устного опроса учащихся.

Вариант I

1. Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам.

2. Выведите формулы координат середины отрезка по координатам его концов.

3. Напишите уравнение окружности с центром в точке В (4; 0), если она проходит через точку А (7; 4).

вариант II

1. Сформулируйте правило нахождения координат разности двух векторов.

2. Выведите формулу для вычисления длины вектора по его координатам.

3. Напишите уравнение прямой, проходящей через две точки А (–3; –3) и В (3; 5).

Вариант III

1. Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам вектора.

2. Выведите уравнение окружности данного радиуса с центром в данной точке, заданной координатами.

3. Найдите координаты середины отрезка АВ, если даны координаты его концов А (–3; 4) и В (3; –6).

Вариант IV

1. Сформулируйте утверждение о разложении произвольного вектора по координатным векторам.

2. Выведите уравнение прямой l в прямоугольной системе координат, если l является серединным перпендикуляром к отрезку с концами А (х ₁; у ₁) и В (х ₂; у ₂).

3. Найдите расстояние между точками М (2; –1) и N (5; –3).

Дата добавления: 2014-12-08