Дифференциальное исчисление

Применение методов дискретной математики в экономике.

При исследовании, анализе и решении управленческих проблем, моделировании объектов исследования и анализа широко используются методы формализированного представления, являющегося предметом рассмотрения в дискретной математике. К ним относятся методы, основанные на теоретико-множественных представлениях, графы, алгоритмы формальные системы, математическая логика.

В экономике существует множество отраслей, использующих методы дискретной математики. Это и эконометрика, и логистика, и математическое моделирование. Так, в эконометрике булевские переменные применяются в исследовании регрессионных моделей с переменной структурой и в построении регрессионных моделей по неоднородным данным. В этом случае рассматривается лишь одно уравнение регрессии, куда вводятся булевские переменные, которые характеризуют изучаемый фактор. Данный метод удобен для выявления зависимости модели от некоторого фактора.

Теория графов широко используется в логистике для описания потоков, задания маршрутов. Так схему дорог удобнее представить в виде ориентированного графа, и известными нам методами выбрать кратчайший путь. В настоящее время, прокладывая маршрут, нельзя не брать во внимание и пропускную способность магистралей, интерпретируя маршруты в графы, можно получить экономически выгодное решение.

При помощи теории нечетких множеств, методом нечеткого предпочтения, можно выбрать конкурентоспособный товар или услугу. Поэтому, данная теория применяется в маркетологии, при исследовании рынков различных экономических благ.

Раздел 3. Основы математического анализа

Общая схема исследования функции и построения ее графика

1. Найти область определения функции. Выделить особые точки (точки разрыва).

2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

3. Найти точки пересечения с осями координат

4. Установить, является ли функция чётной или нечётной.

5. Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).

6. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.

7. Найти точки перегиба и интервалы выпуклости-вогнутости.

8. Найти наклонные асимптоты функции.

9. Построить график функции.

Пример:

Исследовать функцию методами дифференциального исчисления и построить график y = x³+6x²+9x+2

РЕШЕНИЕ:

1) Область определения функции – вся числовая прямая, то есть

D (y) = (−∞; +∞).

Точек разрыва нет, вертикальных асимптот нет.

2) Точки пересечения с осями координат:

Ox: найти затруднительно

Oy:x=0⇒ 0³ +6*0² +9*0+2=2 ⇒ Точка (0;2)

3)Функция общего вида, так как

y(-x) = -x³ +6x² -9x+2≠ ±y(x)

4) Экстремумы и монотонность. Вычисляем первую производную:

y'=3x² +12x+9

Находим критические точки: y'=0; 3x² +12x+9=0; x₁ =-1; x₂ =-3.

Исследуем знак производной на интервалах,

на которые критические точки делят область определения функции.

y' + - +

y -3 -1 x

Функция возрастает на интервалах (−∞;-3),(-1; +∞), убывает на интервале

(-3;-1). Функция имеет минимум в точке x = -1, y(-1) =-2, функция имеет максимум в точке x = -3, y(-3)=2.

5) Выпуклость и точки перегиба. Вычисляем вторую производную.

y''=(3x² +12x+9)'=6x+12

Находим критические точки: y''=0; 6x+12=0; x=-2.

Исследуем знак производной на интервалах, на

которые критические точки делят область определения функции.

y'' - +

y -2 x

Функция выпукла вверх на интервале (−∞;-2), выпукла вниз на интервале

(-2; +∞). Точка перегиба: x =-2, y(-2) = 0.

6) Асимптоты.

Так как 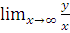= =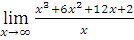∞, асимптот нет.

7) Строим график функции.

x  

Дата добавления: 2014-12-08