Бета-спектров

П4. Математическая модель измерений и обработка

Как видно из рис. 3.2, аппаратурные отклики на b-излучение радиоактивных изотопов представляют собой непрерывные достаточно гладкие функции энергии с некоторой верхней границей Е _bmax, индивидуальной для каждого изотопа. Модель измерений за некоторое время t можно представить в виде суперпозиции

, (П.1)

где Y(Е) – аппаратурный отклик на суммарное излучение из пробы [1/кэВ]; j _j (Е) – аппаратурный отклик на j -й радионуклид [1/с×кэВ(Бк/источник)]; b _j – число распадов j -го радионуклида в измеряемой пробе за время t [ (Бк/источник)×с]; k – число радионуклидов в измеряемой пробе.

В качестве одной из компонент суммирования должен быть и фон измерительной установки. Непосредственно измерить функции Y(Е) и j _j (Е), которые представляют собой функции распределения по энергии, невозможно. Можно измерить только интегралы от этих функций в заранее заданных энергетических интервалах. Поэтому модель измерений следует переписать в виде

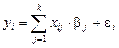, (П.2)

где i – номер энергетического интервала с шириной D Е_i, в пределах которого зарегистрировано y_i импульсов детектора, i = 1, 2, …, n, n – число выбранных для измерений энергетических интервалов; j – номер отдельного излучателя, отклик которого регистрируется детектором; k – число излучателей, куда необходимо включить и фоновую компоненту; b _j – неизвестное число распадов j -го излучателя в источнике за время t проведения измерений, а для фона – умноженное на время t отношение неизвестной средней интенсивности фона в процессе измерений к его интенсивности при контрольных измерениях; x_ij – набор определенных заранее коэффициентов переноса излучения, представляющих собой скорость регистрации детектором импульсов в i -м энергетическом интервале для источника, содержащего только j -й излучатель единичной активности, когда фоновое излучение отсутствует, а для фона − предварительно измеренная его интенсивность в i -м энергетическом интервале; e _i – неизвестная случайная статистическая флуктуация при измерении значения y_i, связанная со статистическим характером процессов излучения, переноса излучения и регистрации в детекторе (не путать с e (Е) – эффективностью регистрации).

Выражение (П.2) представляет собой выборочную реализацию из генеральной совокупности (П.1). Система из n уравнений (3.2) содержит k неизвестных параметров b _j и n неизвестных значений e _i, т.е. (n + k) неизвестных, поэтому решить ее можно только при наложении дополнительных условий, а оценки, полученные после решения, будут только выборочными оценками, а не истинными значениями.

Число энергетических интервалов n может быть велико, а D Е_i = const; в этом случае говорят о чисто спектрометрическом режиме измерений. Если n ограничить, а D Е_i по каким-либо соображениям оптимизации обработки выбирать не обязательно одинаковыми, то реализуется режим радиометра. Используя стандартную спектрометрическую аппаратуру, содержащую амплитудно-цифровые преобразователи (АЦП), удобнее реализовать спектрометрический режим измерений, а обработку в условиях больших статистических флуктуаций при измерениях проб внешней среды лучше организовать в режиме радиометра. При этом, после предварительной энергетической градуировки шкалы АЦП легко реализовать переход от спектрометра к радиометру простым суммированием по соответствующим группам каналов АЦП.

Обозначим вектор результатов измерений y ₁, y ₂, …, y_n, а = b₁, b₂, …, b _n – вектор параметров модели (П.2). В качестве априорных условий при решении системы (П.2) обычно принимаются условия, вытекающие из принципа максимального правдоподобия: в качестве оценок параметров следует принять такие, которые, будучи параметрами генеральной совокупности, позволяют получить конкретную, уже полученную выборочную реализацию с максимальной вероятностью. Для записи функции правдоподобия необходимо знать аналитический вид записи функций распределения для компонент вектора через параметры , т.е. знать законы распределения для флуктуаций компонент в генеральной совокупности. Эти законы распределения будут зависеть от организации самого эксперимента, свойств аппаратуры и, в общем случае, от свойств самого источника излучения.

Если загрузка спектрометрического тракта невелика (1 ¸ 2 кГц) и можно пренебречь совпадениями импульсов от отдельных b-частиц при регистрации, если энергетические окна не перекрываются в процессе перехода от спектрометрического режима измерений к режиму радиометра при обработке, если активность радионуклидов в источнике не изменяется за время измерений и, наконец, если режим работы аппаратуры измерительного тракта достаточно стабилен, то можно положить, что

− компоненты y_i вектора будут статистически независимы между собой, следовательно, некоррелированны;

− случайные величины y_i будут иметь распределение Пуассона.

Тогда функция правдоподобия будет иметь вид произведения пуассоновских распределений для отдельных компонент вектора :

. (П.3)

Дифференцируя L (, ) по компонентам , можно получить систему из k уравнений для нахождения выборочных оценок 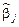, доставляющих максимум L (, ) при конкретном результате измерений вектора . Однако удобнее дифференцировать не L (, ), а ее логарифм (используя свойство монотонности логарифма); система будет иметь то же самое решение, но дифференцировать придется не произведение, а сумму, что значительно проще:

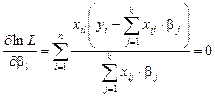, l = 1, 2,..., k. (П.4)

Система (П.4) нелинейна, но допускает численное решение простой итерацией: выбирается начальное приближение для знаменателя, решается линейная система, по ее решению строится новое приближение знаменателя и т.д. Полученные МП-оценки (максимально правдоподобные) обладают всеми свойствами МП-оценок – эффективностью, состоятельностью, асимптотической несмещенностью, асимптотической нормальностью. Но получить одновременно с оценками 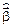оценки дисперсий его компонент и проанализировать качество модели (П.2) в одном итерационном процессе затруднительно.

Если априорные условия дополнить еще одним – числа отсчетов y_i в каждом энергетическом окне достаточно велики (более 20 единиц отсчетов) для аппроксимации пуассоновского распределения нормальным распределением – то можно использовать в записи функции правдоподобия функцию нормального распределения

. (П.5)

Дифференцируя по компонентам , получаем систему уравнений

. (П.6)

Система уравнений (П.6) отличается от (П.4) только формой записи знаменателя, но параметр дисперсии , характеризующий ширину нормального распределения для i -й компоненты вектора , остается неизвестным. Система (П.6) является частным случаем записи уравнений для так называемого метода наименьших квадратов (МНК), математический аппарат которого достаточно хорошо развит.

Метод наименьших квадратов заключается в получении таких оценок параметров генеральной совокупности, при которых квадрат расстояния между вектором измерений и его математическим ожиданием в генеральной совокупности минимален, причем многомерное пространство измерений (размерность пространства равна размерности вектора ) предварительно деформируется так, чтобы все компоненты стали взаимно статистически независимы и имели одинаковую дисперсию (равноточные измерения).

Перепишем модель (П.2) в матричной форме:

, (П.7)

где − n -мерный вектор результатов измерений; − неизвестный k -мерный вектор параметров модели; − неизвестный n -мерный вектор статистических флуктуаций компонент вектора измерений ; Х − n´k -матрица, именуемая матрицей плана эксперимента, k столбцов которой отображают отклики спектрометра на каждый из процессов, формирующих результат измерений при разбиении соответствующих откликов на n энергетических окон; Г − n´n -ковариационная матрица[37] для компонент вектора ; 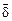− случайный n -мерный вектор, компоненты которого имеют нулевое матожидание и единичную дисперсию.

Ковариационная матрица Г – та самая матрица, которая используется для указанной выше деформации пространства измерений. По ее диагонали располагаются дисперсии компонент , а вне диагонали – ковариации между отдельными компонентами. Квадрат расстояния в деформированном пространстве измерений записывается в виде 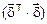, где т – знак транспонирования:

.

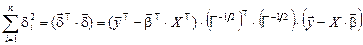Учитывая, что Г – симметричная матрица, получаем

Поскольку , то

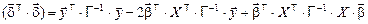. (П.8)

Дифференцируя (3.8) по компонентам и приравнивая производные нулю, получаем систему уравнений

или , (П.9)

решение которой дает МНК-оценки вектора .

Нетрудно заметить, что если преобразовать (П.6) к виду

, (П.10)

получаем эквивалентность уравнений для получения МНК-оценок (П.9) уравнениям для МП-оценок (П.10) для нормальных распределений компонент, где

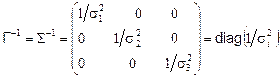. (П.11)

Матрица представляет собой не что иное, как обратную к ковариационной матрицу компонент вектора в высказанных ранее предположениях их статистической независимости (ковариации равны нулю).

Решение линейной системы (П.9) имеет вид

, (П.12)

причем матрица (одно из свойств МНК-оценок)

С = (П.13)

есть ковариационная матрица компонент вектора 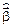оценок параметров модели измерений, по ее диагонали расположены дисперсии соответствующих компонент. Такое свойство позволяет построить доверительные интервалы для истинных (генеральных) значений компонент вектора по их оценкам, имеющим нормальное распределение (еще одно свойство МНК-оценок):

, (П.14)

где − квантиль распределения Стьюдента при уровне значимости e/2 и числе степеней свободы (n − k). Доверительная вероятность для указанного доверительного интервала р = 1 − e.

Поскольку после проведения эксперимента дисперсии компонент вектора измерений нам неизвестны, воспользуемся тем, что эти компоненты имеют пуассоновское распределение, тогда в качестве оценки дисперсии величины y_i можно принять само значение y_i вместо его математического ожидания в генеральной совокупности (если значения y_i достаточно велики – не менее 50 зарегистрированных в энергетическом окне событий). Ковариационная матрица (ее оценка) приобретает вид

Г = . (П.15)

Выражения (П.12) – (П.15) представляют собой модель обработки спектров. При этом компоненты вектора − числа зарегистрированных импульсов в энергетических окнах за все время измерений; компоненты полученного вектора оценок 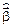− числа распадов соответствующих радионуклидов за все время измерений. Нам же требуется определить удельную активность радионуклидов в образце, поэтому удобнее перейти к другим переменным:

u_i = y_i / t, b_j = b _j/t,

где u_i - скорость счета, а b_j - скорость распада нуклида. Модель измерений (П.7) приобретает вид

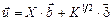, (П.16)

а результат МНК-подгонки

, (П.17)

где

− (П.18)

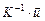ковариационная матрица для компонент скоростей счета . Произведение в (П.17) можно преобразовать к виду

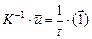, (П.19)

где − n -мерный вектор из единиц. Следовательно, вместо (П.17) можно записать

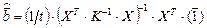. (П.20)

Ковариационная матрица для компонент имеет тот же вид, что и (П.13) с заменой Г^-1 на К^-1:

, (П.21)

а доверительный интервал аналогичен (3.14) с заменой b на b:

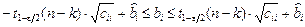. (П.22)

В качестве матрицы Х плана эксперимента используется построенная по материалам предварительных градуировочных измерений фона и образцовых источников матрица, столбцы которой суть скорость счета фона в энергетических окнах и нормированная на известную удельную активность градуировочных источников скорость счета от источников в тех же энергетических окнах после вычета фона.

ПРИНЯТЫЕ СОКРАЩЕНИЯ

АЦП – амплитудно-цифровой преобразователь

ВВЭР – водо-водяной энергетический реактор

ЖКТ – желудочно-кишечный тракт

ИДК – индивидуальный дозиметрический контроль

ИРГ – инертные радиоактивные газы

КГО – контроль герметичности оболочек

МКРЗ – Международная комиссия по радиологической защите

МНК – метод наименьших квадратов

МП – максимальное правдоподобие

ОБЭ – относительная биологическая эффективность

ОСГИ – образцовые спектрометрические гамма-источники

ОЯТ – отработавшее ядерное топливо

ПГП – предел годового поступления

ПД – продукты деления

ППП – пик полного поглощения

ППР – планово-предупредительный ремонт

ПХИ – пик характеристического излучения

ППД – полупроводниковый детектор

РБМК – реактор большой мощности канальный

РФА – рентгено-флюоресцентный анализ

СИЧ – счетчик излучения человека

ТВС – тепловыделяющая сборка

ЦТП – центр тяжести пика

ФЭУ – фотоэлектронный умножитель

ЯТЦ – ядерный топливный цикл

СОДЕРЖАНИЕ

ВВЕДЕНИЕ……………………………………………………….3

Работа 1. СПЕКТРОМЕТРИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ГАММА-ИЗЛУЧАЮЩИХ НУКЛИДОВ В ОБЪЕКТАХ ОКРУЖАЮЩЕЙ СРЕДЫ ………………………………………15

Работа 2. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ПОЛУПРОВОДНИКОВОГО СПЕКТРОМЕТРА ……………..61

Работа 3. БЕТА-СПЕКТРОМЕТРИЧЕСКОЕ ИЗМЕРЕНИЕ СОДЕРЖАНИЯ СТРОНЦИЯ-90 В ПРОБАХ ВНЕШНЕЙ СРЕДЫ……………………………………………………………81

Работа 4. ОПРЕДЕЛЕНИЕ СОДЕРЖАНИЯ РАДИОНУКЛИДОВ В ОРГАНАХ ЧЕЛОВЕКА И ОЦЕНКА ОЖИДАЕМОЙ ЭФФЕКТИВНОЙ ДОЗЫ ВНУТРЕННЕГО ОБЛУЧЕНИЯ..…110

ПРИЛОЖЕНИЕ…………………………………………………136

Редактор З.И.Сныкова

Компьютерная верстка Е.Л.Борисенко

ЛР №020713 от 27.04.1998 Подписано к печати Формат бум. 60´84/16 Печать Бумага KYMLUX Печ. л. Зак. № Тираж 100 экз. Цена договорная

Отдел множительной техники ИАТЭ, 249035, г.Обнинск, Студгородок, 1.

[1] Для определения малых количеств элементов метод РФА используется редко, т.к. в диапазоне содержаний < 10^-4 он уступает по своим возможностям другим физическим методам.

[2] Спектрометрические анализы проб внешней среды также позволяют определять степень происшедшей аварии на объектах ЯТЦ; это может быть весьма актуальным, т.к. не всегда есть возможность сразу определить причины аварии и масштаб произведенных разрушений.

[3] Подвергается переработке только топливо ВВЭР.

[4] Если в результате радиоактивного распада ядер N ₁ возникают тоже радиоактивные ядра N ₂, то радиоактивное равновесие между ними наступает тогда, когда число распадов дочернего вещества l₂ N ₂ равно числу распадов материнского вещества l₁ N ₁. Уравнение l₁ N ₁ = l₂ N ₂ носит название векового равновесиия.

[5] Дельта-функция Дирака была введена для описания переходов между возбужденными состояниями:

, причем, а.

Представление спектра в виде d-функции оправдано тем, что время жизни возбужденных состояний (в ядерном масштабе) достаточно велико (t > 10^-15 с) и неопределенность D Е ~ ħ/t в величине энергии не превышает ~ 1 эВ, а энергии g-квантов находятся в диапазоне от нескольких десятков килоэлектронвольт до нескольких мегаэлектронвольт.

[6] Здесь m_ec ² - энергия покоя электрона (позитрона),2 m_ec ² = 1,022 МэВ.

[7] Электроны Оже испускаются в процессе непосредственной передачи энергии возбуждения атома одному из его внешних электронов (без предварительного испускания фотона).

[8] Этот процесс в вакууме невозможен, т.к. в этом случае не будет выполняться закон сохранения импульса.

[9] Асимметричность пика полного поглощения обусловлена неполным собиранием заряда в детекторе, наложением импульсов в спектрометрическом тракте и т.д.

[10] Т.е. не происходит, например, совпадения импульсов от нескольких g-квантов и т.д.

[11] Не следует путать аппаратурный спектр f(A), который мы видим на экране, с функцией отклика G (A,E ₀), которая может быть получена только в случае, когда на детектор попадают g-кванты одной энергии Е ₀, при полной невозможности попадания в детектор рассеянного в источнике и защите излучения.

[12] Центр тяжести пика находится по формуле ЦТП =, где i – номер канала анализатора, N_i – число импульсов в канале. Для симметричных пиков ЦТП равен номеру канала, в котором находится максимальное значение N_i.

[13] Средняя квадратическая ошибка суммы (или разности) двух независимых величин равна корню квадратному из суммы дисперсий отдельных слагаемых, т.е., если Z = X – Y, то D (Z) = D (X) + D (Y), или s(Z) =.

[14] Современные программы обработки g-спектров имеют обширные таблицы, содержащие характеристики всех g-излучающих радионуклидов, появление которых возможно в исследуемых пробах. Эти таблицы называются библиотеками нуклидов, они используются в программах по автоматической расшифровке g-спектров.

[15] Эффективность спектрометра не следует путать с эффективностью детектора, которая определяется как отношение числа зарегистрированных импульсов к числу частиц, попавших в детектор.

[16] Плотность вещества в чувствительном объеме ППД на три порядка выше, чем в ионизационной камере.

[17] В отличие от металлов, у которых электропроводность с ростом температуры уменьшается.

[18] Носители электрического заряда в полупроводнике обозначаются: n – электроны, p – дырки.

[19] Диффузионные способности носителей зависят от многих факторов, например, от температуры, количества примесей и т.д.

[20] Описываемый р - n -переход нельзя создать механически, соединив два образца. Так, например, для изготовления диффузионных детекторов требуется температура до 800 ⁰С.

[21] Шумовые токи ППД складываются из тепловых шумов и шумов, связанных с токами утечки через переход.

[22] В настоящее время для осуществления радиационного контроля за содержанием нуклидов естественного и техногенного происхождения в различных объектах окружающей среды и технологических сред разработаны различные математические программы автоматической обработки g-спектров. Как правило, результатом работы подобных программ является перечень радионуклидов, находящихся в пробе, и их удельное содержание. Методы достижения подобных результатов многообразны, часто при решении используются достаточно сложные математические выкладки. Обычно программа автоматизированной обработки спектров снабжается «библиотекой нуклидов», содержащей все нуклиды, которые могут быть теоретически найдены в исследуемой пробе (для этого обычно указывается тип пробы: почва вблизи АЭС, вода из технологического канала и т.д.).

Как правило, основными этапами работы программы обработки спектров являются нахождение одиночных ППП (очень важно корректное определение границ пика), определение характеристик этих пиков (площадь ППП, ЦТП для определения энергии, идентификация пиков при помощи «библиотеки нуклидов»), по известной эффективности регистрации расчет удельной активности, далее следует расшифровка дублетов и более сложных образований, если в этом есть необходимость. Учитывая, что важнейшие эксплуатационные характеристики ППД и сцинтилляционных детекторов − энергетическое разрешение, эффективность и чувствительность регистрации – отличаются более, чем на порядок, подходы к составлению программ обработки для этих детекторов принципиально отличаются. Хотя в настоящее время делаются попытки создать универсальную программу автоматической обработки любой спектрометрической информации. На самом деле, даже для полупроводниковых g-спектрометров полная автоматизация измерений радионуклидов в смесях произвольного, заранее не известного состава, во всяком случае при существующем уровне развития техники, представляется технической утопией.

[23] Кумулятивный выход равен сумме собственного независимого выхода изотопа плюс независимые выходы всех его предшественников.

[24] Радионуклид ¹⁴С образуется при захвате азотом воздуха нейтронов, испускаемых во время ядерного взрыва: ¹⁴N(n,p)¹⁴C, максимальная энергия испускаемых b-частиц Е _bmax = 156,5 кэВ.

[25] ¹⁰⁶Ru и ¹⁴⁴Pr испускают наиболее жесткие b-частицы.

[26] Электроны внутренней конверсии возникают, когда энергия возбуждения ядра непосредственно (без предварительного испускания g-кванта) передается орбитальному электрону.

[27] ¹³⁷Cs испускает b-частицы с максимальной энергией 511 кэВ (94,43 %), имеет Т _1/2 = 30 лет, превращается в ^137mВа, испускающий g-кванты с энергией 661 кэВ (85 %) и имеющий Т _1/2 = 2,55 мин.

[28] Размерность матрицы плана эксперимента Х в этом случае n ´3, три ее столбца соответствуют отклику на фон установки, ⁹⁰Y и ⁴⁰К, а n строк соответствуют n энергетическим окнам (см. прил. п4).

[29] Полученные результаты за вычетом предварительно определенного фона установки определяют столбцы матрицы плана эксперимента Х, соответствующие ⁹⁰Y и ⁴⁰K (см. прил. п4).

[30] По результатам измерений исследуемых образцов формируется вектор и оценивается матрица К в модели (3.16) (см. прил. п4).

[31] Международная комиссия по радиологической защите.

[32] Депонирование - отложение, сохранение.

[33] Если ввести полупериод поглощения t – время, за которое в жидкостях тела в среднем поглощается 50 % вещества, растворимость можно охарактеризовать следующим образом: тип «М» t ~ 7000 сут; тип «Б» t = 10 мин; «П» − при растворении в легких человека веществ, отнесенных к этому типу, 10 % их массы поглощается с полупериодом 10 мин и 90 % - с полупериодом 140 сут.

[34] ОБЭ - отношение поглощенной дозы D ₀ образцового излучения, вызывающей определенный биологический эффект, к поглощенной дозе D рассматриваемого излучения, вызывающей такой же биологический эффект. В качестве образцового излучения используют рентгеновское излучение с граничной энергией 200 кэВ.

[35] При ППР реактор останавливается и теплоноситель выводится из трубопровода.

[36] Эффективная доза Е – величина, используемая как мера риска возникновения отдаленных последствий облучения всего тела человека и отдельных его органов и тканей с учетом их радиочувствительности. Она представляет сумму произведений эквивалентной дозы в органах и тканях на соответствующие взвешивающие коэффициенты: Е =. Значения w _Т установлены примерно равными отношению эквивалентной дозы равномерного облучения всего тела стандартного человека и эквивалентной дозы Н _Т облучения органа или ткани Т, при которых ожидается один и тот же ущерб вследствие сокращения продолжительности жизни человека в результате возникновения отдаленных эффектов, вызванных облучением. Единица эффективной дозы – зиверт (Зв).

[37] Ковариация k_xy двух случайных величин х и y равна k_xy = =, она служит измерителем степени тесноты статистической связи между случайными величинами x и y. Свойство: k_xy = k_yx. Для независимых случайных величин k_xy = 0, k_xх =. Ковариации k_ij вместе с дисперсиями образуют симметричную ковариационную матрицу размером n ´ n. Если случайные величины х ₁,..., х_n попарно некоррелированы, то ковариационная матрица имеет диагональный вид.

Дата добавления: 2014-12-08